出处:Paddle文档平台 - 自注意力机制
在前边所讲的内容中,会使用一个查询向量 $q$ 和对应的输入 $H=[h_1,h_2,...,h_n]$ 进行attention计算,这里的查询向量$q$往往和任务相关,比如基于Seq-to-Seq的机器翻译任务中,这个查询向量$q$可以是Decoder端前个时刻的输出状态向量,如图1所示。
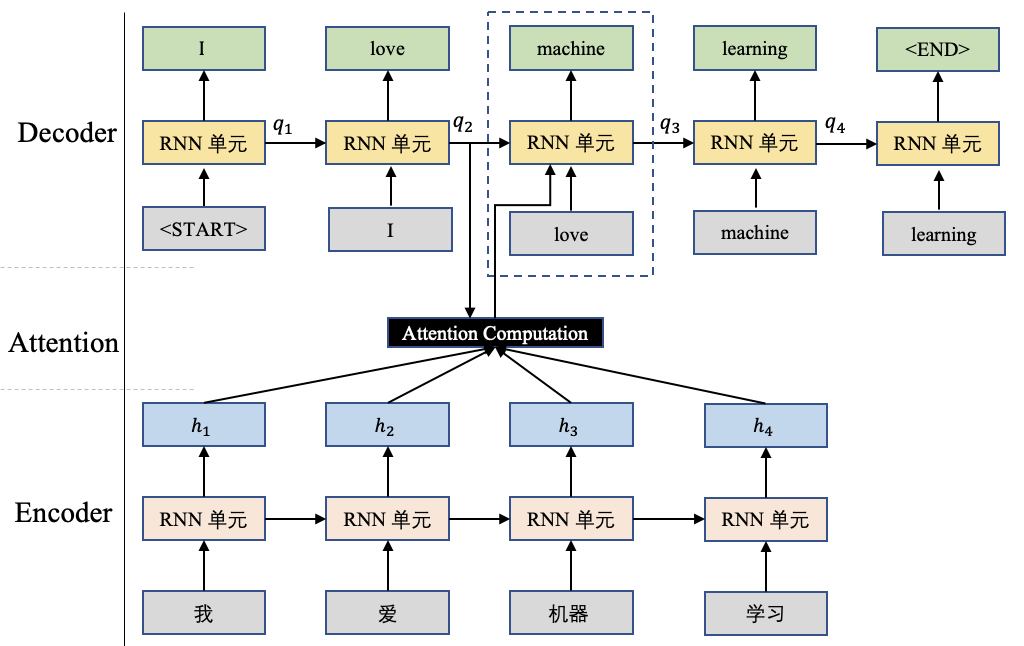
图1 机器翻译示例图
然而在自注意力机制(self-Attention)中,这里的查询向量也可以使用输入信息进行生成,而不是选择一个上述任务相关的查询向量。相当于模型读到输入信息后,根据输入信息本身决定当前最重要的信息。
自注意力机制往往采用查询-键-值(Query-Key-Value)的模式,不妨以BERT中的自注意力机制展开讨论,如图2所示。
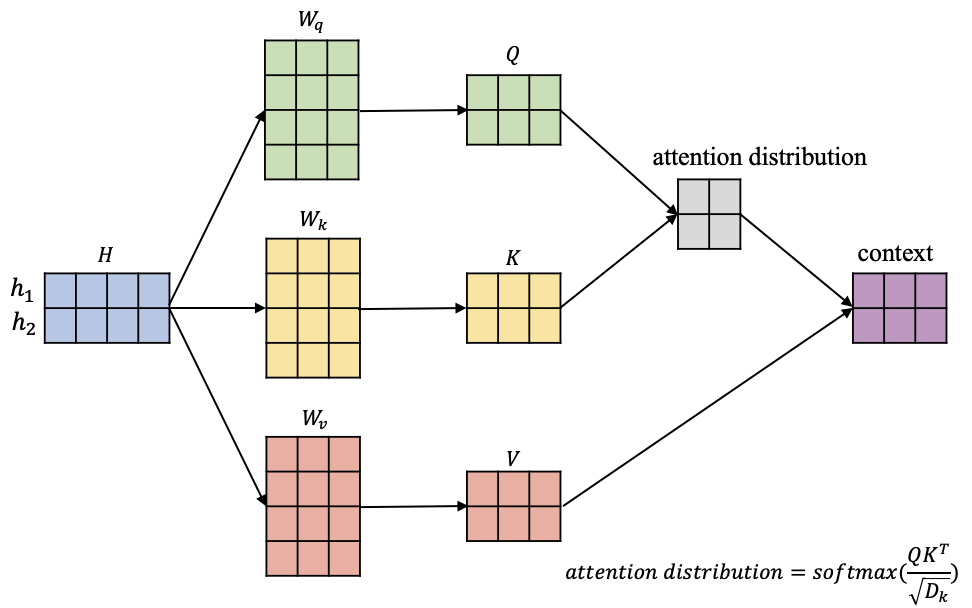
图2 自注意力机制的计算过程
在图2中,输入信息$H=[h_1,h_2]$,其中蓝色矩阵中每行代表对应一个输入向量,另外图2中有 $W_q,W_k,W_v$ 3个矩阵,它们负责将输入信息 $H$ 依次转换到对应的查询空间 $Q=[q_1,q_2]$ ,键空间 $K=[k_1,k_2]$和值空间$V=[v_1,v_2]$ :
$$ \left[ \begin{matrix} q_1 = h_1W_q \\ q_2=h_2W_q \end{matrix} \right] \Rightarrow Q=HW_q $$
$$ \left[ \begin{matrix} k_1 = h_1W_k \\ k_2=h_2W_k \end{matrix} \right] \Rightarrow K=HW_k $$
$$ \left[ \begin{matrix} v_1 = h_1W_v \\ v_2=h_2W_v \end{matrix} \right] \Rightarrow V=HW_v $$
在获得输入信息在不同空间的表达 $Q$ 、 $K$ 和 $V$ 后,这里不妨以 $h_1$ 这个为例,去计算这个位置的一个attention输出向量 $context_1$ ,它代表在这个位置模型应该重点关注的内容,如图3所示。
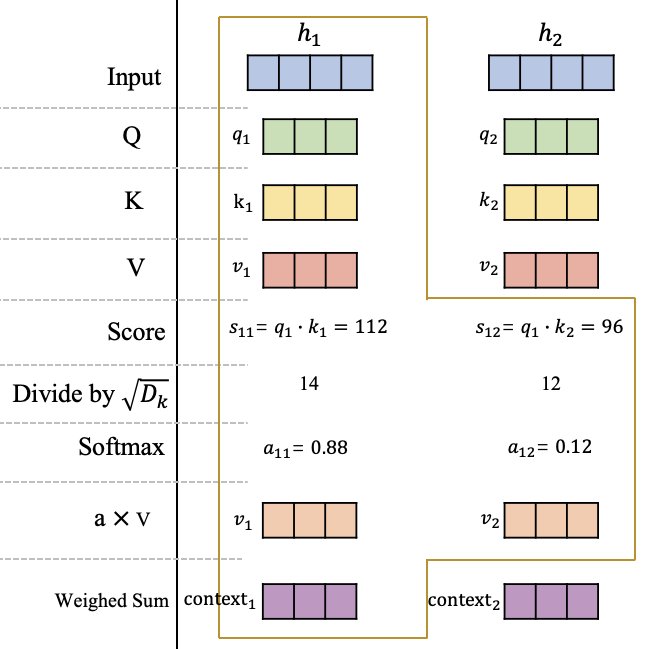
图3 自注意力机制的详细计算过程
可以看到在获得原始输入 $H$ 在查询空间、键空间和值空间的表达 $Q$ 、 $K$ 和 $V$ 后,计算 $q_1$ 在 $h_1$ 和 $h_2$ 的分数 $s_{11}$ 和 $s_{12}$ ,这里的分数计算采用的是点积操作。然后将分数进行缩放并使用softmax进行归一化,获得在$h_1$这个位置的注意力分布: $a_{11}$ 和 $a_{12}$,它们代表模型当前在$h_1$这个位置需要对输入信息$h_1$和 $h_2$的关注程度。最后根据该位置的注意力分布对 $v_1$和 $v_2$进行加权平均获得最终$h_1$这个位置的Attention向量 $context_1$ 。
同理,可以获得第2个位置的Attention向量 $context_2$,或者继续扩展输入序列获得更多的 $context_i$,原理都是一样的。
讨论到这里,相信已经知道什么是注意力机制了,但是为了正式一点,重新组织一下注意力机制的计算过程。
假设当前有输入信息$H=[h_1,h_2,...,h_n]$,我们需要使用自注意力机制获取每个位置的输出$context=[context_1, context_2,...,context_n]$。
首先,需要将原始输入映射到查询空间$Q$、键空间$K$和值空间$V$,相关计算公式如下:
$$ Q=HW_q =[q_1,q_2,...,q_n] \\ K=HW_k =[k_1,k_2,...,k_n]\\ V=HW_v =[v_1,v_2,...,v_n] $$
接下来,我们将去计算每个位置的注意力分布,并且将相应结果进行加权求和:
$$ context_i=\sum_{j=1}^n softmax(s(q_i, k_j)) \cdot v_j $$
其中 $s(q_i,k_j)$是经过上述点积、缩放后分数值。
最后,为了加快计算效率,这里其实可以使用矩阵计算的方式,一次性计算出所有位置的的Attention输出向量:
$$ context=softmax(\frac{QK^T}{\sqrt{D_k}})V $$