出处:Paddle文档平台 - 注意力机制
1. 注意力机制是什么
假设有一天热爱绘画的你决定去户外写生,你来到一片山坡上,极目远去,心旷神怡。头顶一片蔚蓝,脚踩一席草绿,远处山川连绵,眼前花草送香,暖阳含羞云后,轻风拂动衣襟,鸟啼虫鸣入耳,美景丹青共卷。

图1《起风了》插图
你集中精神,拿起画笔将蓝天、白云、青草等等这些元素,按照所思所想纷纷绘入画板。在绘画的过程中,你会持续地关注你构思到画板上的元素(比如蓝天,白云),而不会太多关注那些其他的元素,比如风,虫鸣,阳光等等。即你的精神是聚焦在你关心的那些事物上,这其实就是注意力的体现,这种有意识的聚焦被称为聚焦式注意力(Focus Attention)。
然而,正当你在画板上忘我倾洒的时侯,突然有人在背后喊你的名字,你立马注意到了,然后放下画笔,转头和来人交谈。这种无意识地,往往由外界刺激引发的注意力被称为显著性注意力(Saliency-Based Attention)。
但不论哪一种注意力,其实都是让你在某一时刻将注意力放到某些事物上,而忽略另外的一些事物,这就是注意力机制(Attention Mechanism)。
在深度学习领域,模型往往需要接收和处理大量的数据,然而在特定的某个时刻,往往只有少部分的某些数据是重要的,这种情况就非常适合Attention机制发光发热。
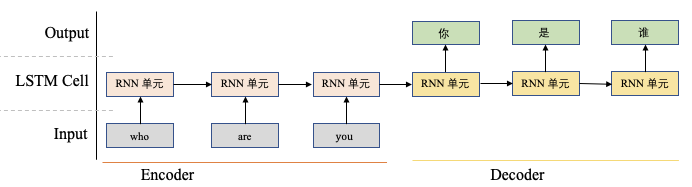
图2 机器翻译任务
举个例子,图2展示了一个机器翻译的结果,在这个例子中,我们想将"who are you"翻译为"你是谁",传统的模型处理方式是一个seq-to-seq的模型,其包含一个encoder端和一个decoder端,其中encoder端对"who are you"进行编码,然后将整句话的信息传递给decoder端,由decoder解码出"我是谁"。在这个过程中,decoder是逐字解码的,在每次解码的过程中,如果接收信息过多,可能会导致模型的内部混乱,从而导致错误结果的出现。
我们可以使用Attention机制来解决这个问题,从图2可以看到,在生成"你"的时候和单词"you"关系比较大,和"who are"关系不大,所以我们更希望在这个过程中能够使用Attention机制,将更多注意力放到"you"上,而不要太多关注"who are",从而提高整体模型的表现。
备注:在深度学习领域,无意识的显著性注意力更加常见。
Attention机制自提出以来,出现了很多不同Attention应用方式,但大道是共同的,均是将模型的注意力聚焦在重要的事情上。本文后续将选择一些经典或常用的Attention机制展开讨论。
2. 经典注意力机制
2.1. 用机器翻译任务来看Attention机制的计算
单独地去讲Attention机制会有些抽象,也有些枯燥,所以不妨以机器翻译任务为例,通过讲解Attention机制在机器翻译任务中的应用方式,来了解Attention机制的使用。
什么是机器翻译任务?以中译英为例,机器翻译是将一串中文语句翻译为对应的英文语句,如图1所示。
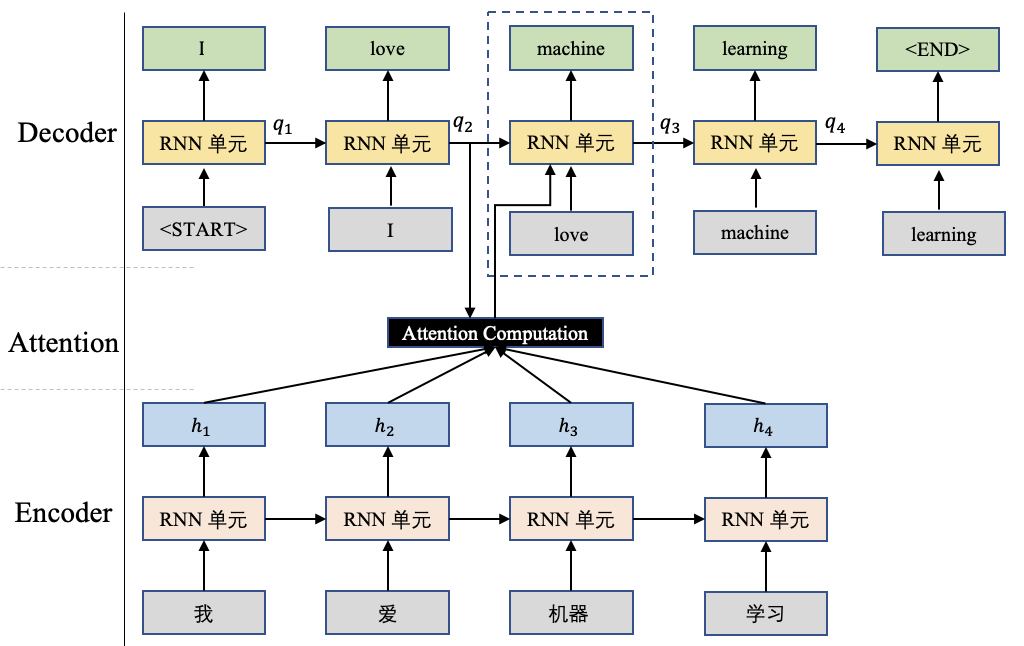
图3 机器翻译示例图
图3展示了一种经典的机器翻译结构Seq-to-Seq,并且向其中添加了Attention计算。Seq-to-Seq结构包含两个部分:Encoder和Decoder。其中Encoder用于将中文语句进行编码,这些编码后续将提供给Decoder进行使用;Decoder将根据Encoder的数据进行解码。
还是以上图3为例详细解释一下Decoder的解码过程。
更明确的讲,图3展示的是生成单词"machine"时的计算方式。首先将前一个时刻的输出状态 $q_2$ 和Encoder的输出 $h=[h_1,h_2,h_3,h_4]$ 进行Attention计算,得到一个当前时刻的 $context$ ,用公式可以这样组织:
$$ \begin{align} [a_1,a_2,a_3,a_4] &= softmax([s(q_2, h_1), s(q_2,h_2),s(q_2, h_3),s(q_2, h_4)]) \\ context&=\sum_{i=1}^4 a_i \cdot h_i \end{align} $$
我们来解释一下,这里的 $s(q_i,h_j)$ 表示注意力打分函数,它是个标量,其大小描述了当前时刻在这些Encoder的结果上的关注程度,这个函数在后边会展开讨论。然后用softmax对这个结果进行归一化,最后使用加权评价获得当前时刻的上下文向量 $context$。这个$context$可以解释为:截止到当前已经有了"I love",在此基础上下一个时刻应该更加关注源中文语句的那些内容。这就是关于Attention机制的一个完整计算。
最后,将这个$context$和上个时刻的输出"love"进行融合作为当前时刻RNN单元的输入。
图3中采用了继续融合上一步的输出结果,例如上述描述中融合了"love",在有些实现中,并没有融入这个上一步的输出,默认 $q_2$ 中已经携带了"love"的信息,这也是合理的。
2.2. 注意力机制的正式引入
前边我们通过机器翻译任务介绍了Attention机制的整体计算。但是还有点小尾巴没有展开,就是那个注意力打分函数的计算,现在我们将来讨论这个事情。但在讲这个函数之前,我们先来对上边的Attention机制的计算做个总结,图4详细地描述了Attention机制的计算原理。
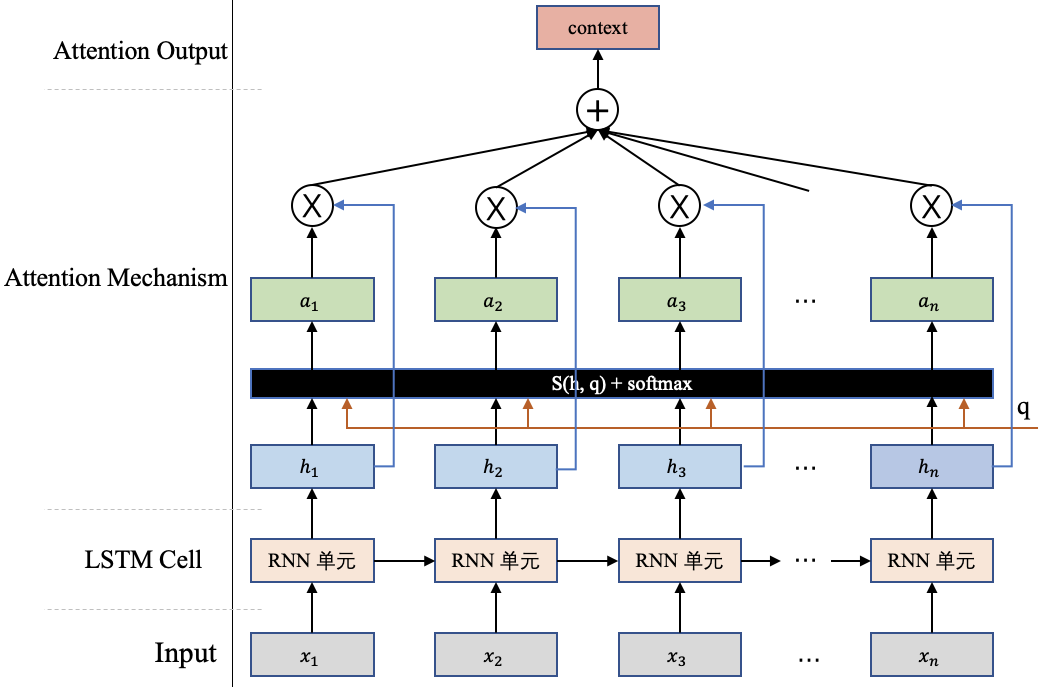
假设现在我们要对一组输入 $H=[h_1,h_2,h_3,...,h_n]$使用Attention机制计算重要的内容,这里往往需要一个查询向量 $q$(这个向量往往和做的任务有关,比如机器翻译中用到的那个 $q_2$ ) ,然后通过一个打分函数计算查询向量 $q$ 和每个输入 $h_i$ 之间的相关性,得出一个分数。接下来使用softmax对这些分数进行归一化,归一化后的结果便是查询向量 $q$在各个输入 $h_i$上的注意力分布 $a=[a_1,a_2,a_3,...,a_n]$,其中每一项数值和原始的输入$H=[h_1,h_2,h_3,...,h_n]$一一对应。以 $a_i$ 为例,相关计算公式如下:
$$ \begin{align}a_i = softmax(s(h_i, q))= \frac {exp(s(h_i,q))} {\sum_{j=1}^n exp(s(h_j, q))} \end{align} $$
最后根据这些注意力分布可以去有选择性的从输入信息 $H$ 中提取信息,这里比较常用的信息提取方式,是一种"软性"的信息提取(图4展示的就是一种"软性"注意力),即根据注意力分布对输入信息进行加权求和,最终的这个结果 $context$ 体现了模型当前应该关注的内容:
$$ context = \sum_{i=1}^n a_i \cdot h_i $$
现在我们来解决之前一直没有展开的小尾巴-打分函数,它可以使用以下几种方式来计算:
- 加性模型: $s(h, q) = v^Ttanh(Wh+Uq)$
- 点积模型: $s(h, q) = h^Tq$
- 缩放点积模型: $s(h, q) =\frac{ h^Tq}{\sqrt D}$
- 双线性模型: $s(h, q) = h^TWq$
以上公式中的参数 $W$、$U$和$v$均是可学习的参数矩阵或向量,$D$为输入向量的维度。下边我们来分析一下这些分数计算方式的差别。
加性模型引入了可学习的参数,将查询向量 $q$ 和原始输入向量 $h$ 映射到不同的向量空间后进行计算打分,显然相较于加性模型,点积模型具有更好的计算效率。
另外,当输入向量的维度比较高的时候,点积模型通常有比较大的方差,从而导致Softmax函数的梯度会比较小。因此缩放点积模型通过除以一个平方根项来平滑分数数值,也相当于平滑最终的注意力分布,缓解这个问题。
最后,双线性模型可以重塑为$s(h_i, q) = h^TWq=h^T(U^TV)q=(Uh)^T(Vq)$,即分别对查询向量 $q$ 和原始输入向量 $h$进行线性变换之后,再计算点积。相比点积模型,双线性模型在计算相似度时引入了非对称性。
3. 注意力机制的一些变体
3.1. 硬性注意力机制
在经典注意力机制章节使用了一种软性注意力的方式进行Attention机制,它通过注意力分布来加权求和融合各个输入向量。
而硬性注意力(Hard Attention)机制则不是采用这种方式,它是根据注意力分布选择输入向量中的一个作为输出。这里有两种选择方式:
- 选择注意力分布中,分数最大的那一项对应的输入向量作为Attention机制的输出。
- 根据注意力分布进行随机采样,采样结果作为Attention机制的输出。
硬性注意力通过以上两种方式选择Attention的输出,这会使得最终的损失函数与注意力分布之间的函数关系不可导,导致无法使用反向传播算法训练模型,硬性注意力通常需要使用强化学习来进行训练。因此,一般深度学习算法会使用软性注意力的方式进行计算,
3.2. 键值对注意力机制
假设我们的输入信息不再是前边所提到的$H=[h_1,h_2,h_3,...,h_n]$ ,而是更为一般的键值对(key-value pair)形式 $(K,V)=[(k_1,v_1),(k_2,v_2),...,(k_n,v_n)]$ ,相关的查询向量仍然为 $q$。这种模式下,一般会使用查询向量 $q$和相应的键 $k_i$进行计算注意力权值 $a_i$。
$$ \begin{align} a_i=softmax(s(k_i,q)) = \frac{exp(s(k_i,q))}{\sum_{j=1}^n exp(s(k_j, q))} \end{align} $$
当计算出在输入数据上的注意力分布之后,利用注意力分布和键值对中的对应值进行加权融合计算:
$$ context=\sum_{i=1}^n a_i \cdot v_i $$
显然,当键值相同的情况下$k=v$,键值对注意力就退化成了普通的经典注意力机制。
3.3. 多头注意力机制
多头注意力(Multi-Head Attention)是利用多个查询向量 $Q=[q_1,q_2,...,q_m]$,并行地从输入信息$(K,V)=[(k_1,v_1),(k_2,v_2),...,(k_n,v_n)]$中选取多组信息。在查询过程中,每个查询向量 $q_i$ 将会关注输入信息的不同部分,即从不同的角度上去分析当前的输入信息。
假设 $a_{ij}$代表第 $i$ 各查询向量 $q_i$ 与第 $j$ 个输入信息 $k_j$ 的注意力权重, $context_i$ 代表由查询向量$q_i$计算得出的Attention输出向量。其计算方式为:
$$ \begin{align} a_{ij}=softmax(s(k_j,q_i)) &= \frac{exp(s(k_j,q_i))}{\sum_{t=1}^n exp(s(k_t, q_i))} \\ context_i &=\sum_{j=1}^n a_{ij} \cdot v_j \end{align} $$
最终将所有查询向量的结果进行拼接作为最终的结果:
$$ context=context_1 \oplus context_2 \oplus context_3 \oplus...\oplus context_m $$
公式里的 $\oplus$表示向量拼接操作。