论文:Divide and Conquer the Embedding Space for Metric Learning - CVPR2019
补充材料:Divide and Conquer the Embedding Space for Metric Learning - Supplementary Material
Slides:Identification of Humpback Whales using Deep Metric Learning
主要是对 Slides 中的内容的学习. 主要包括三方面的内容:
[1] - 度量学习问题简述
[2] - 度量学习中的采样问题
[3] - 嵌入空间分而治之的度量学习方法(Divide and Conquer the Embedding Space for Metric Learning)
1. 度量学习问题简述
如何比较图像?


上面这些图像间的相似性(不相似性)是怎样的呢?
最直接的方法是,将图像投影到 d 维欧式空间,计算欧式距离以表示相似性度量.

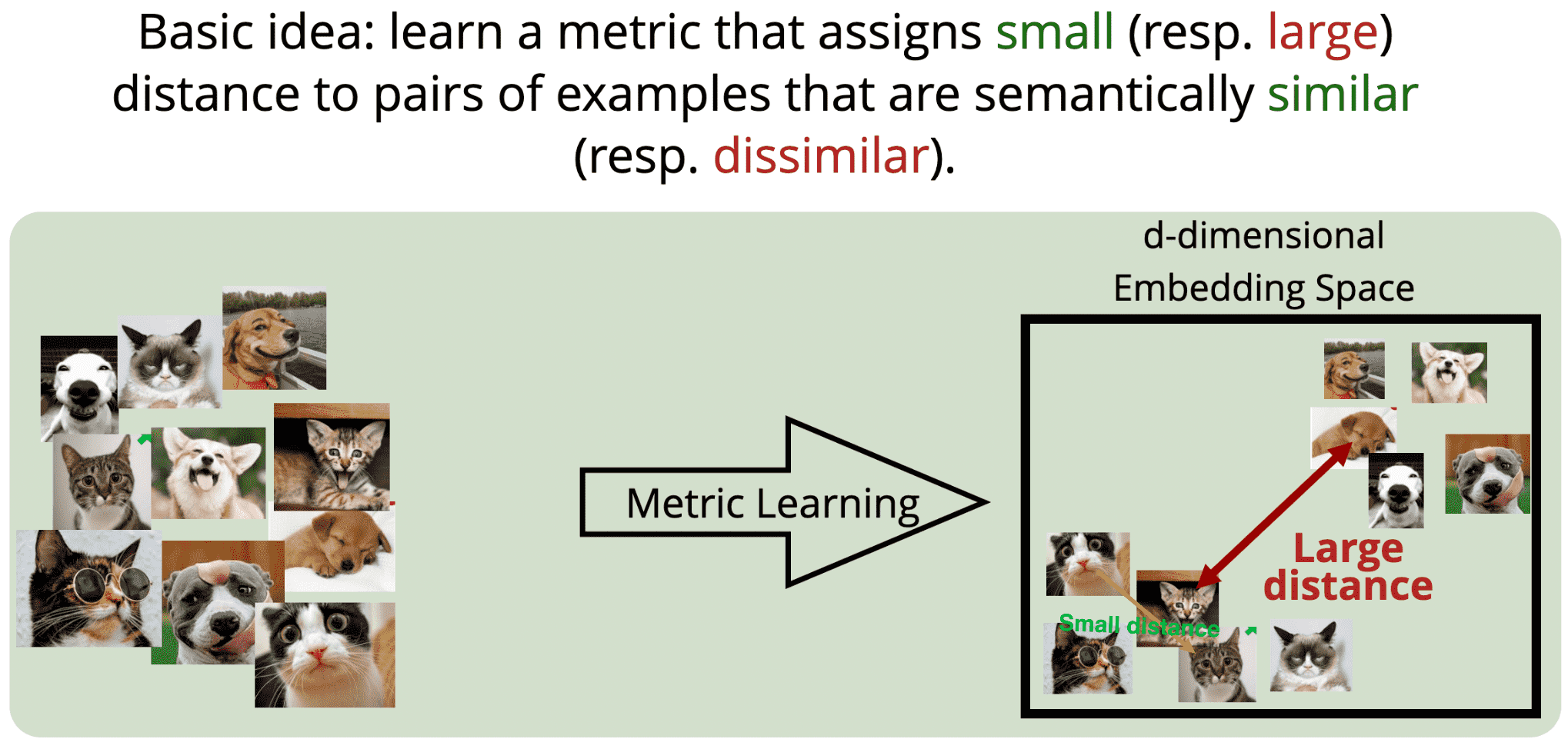
度量学习,就是用于比较图像相似性.
最基本的思想,学习一种度量,将语义相似的样本对之间的距离缩小;而不相似样本对之间的距离扩大.
度量学习的应用领域如,手写字体识别、身份鉴定、图像搜索等.
其用途是,给定一张图像,从已有图像库中找到最相似的图像.

度量学习的网络结构如:
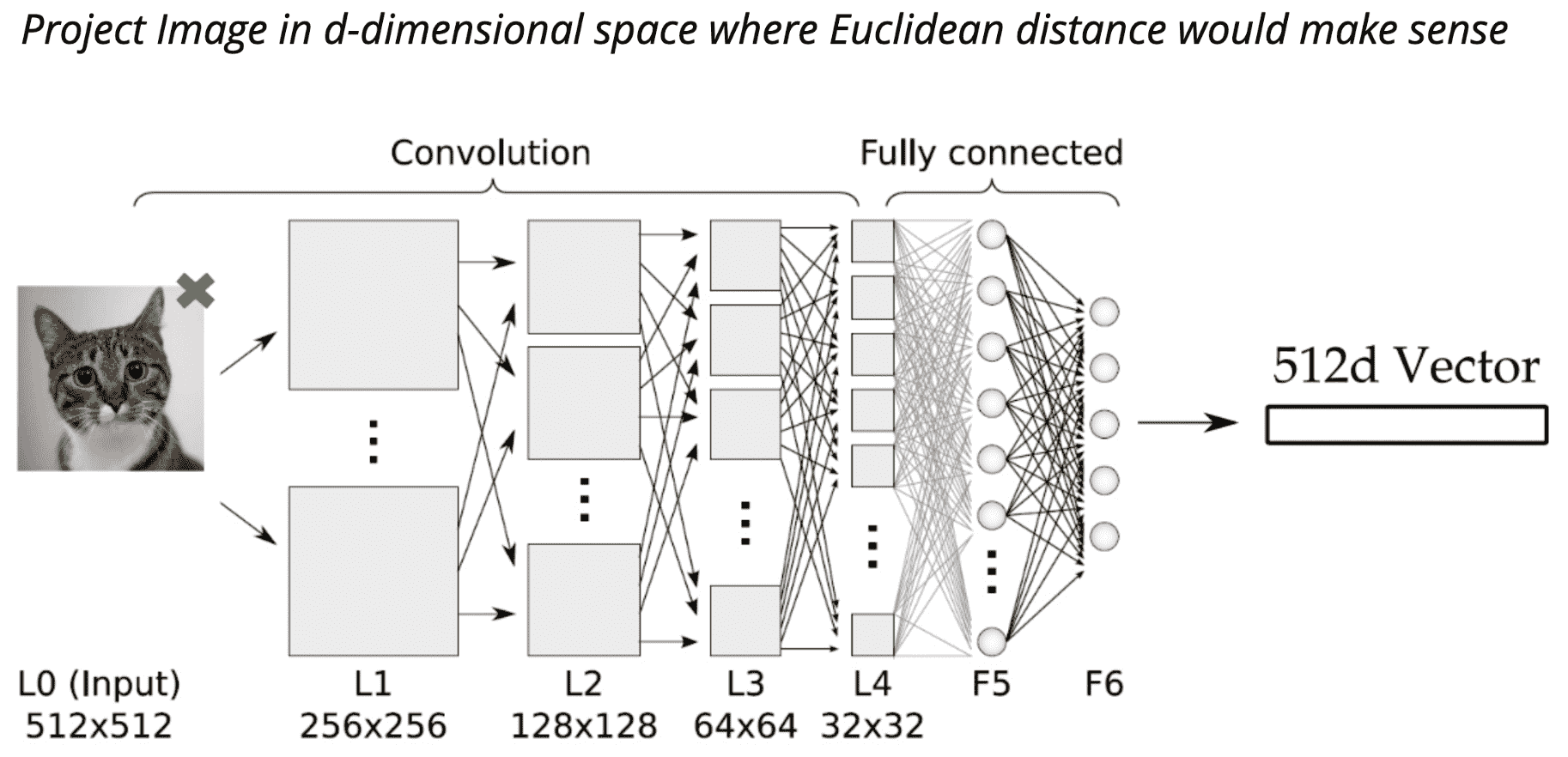
每一网络层构成上一网络层的特征表示,以学习更高层次的抽象.
从图像空间映射到特征空间(嵌入空间),Pixels -> Edges -> Contours -> Object parts -> Embedding Space.
局部特征到全局特征(Local Features - Global Features).
采用 Triplet loss 函数的度量学习模型训练:

采用孪生网络(Siamese Network)训练:

2. 度量学习中的采样问题
为什么需要进行采样?

上面这种容易区分的开,但下图示的就比较难区分了.

在度量学习中加入采样层,


假设数据集大小为 N,训练集中共有 N3 个可能的三元组.
无需随机采样,因为只有一小部分三元组是有意义的,是非零loss的.
难三元组(hard triplets) 的选择是非常重要的,其有助于提升模型能力. 该如何去做呢?
第一种方式是,难负样本采样(Hard Negative Sampling).
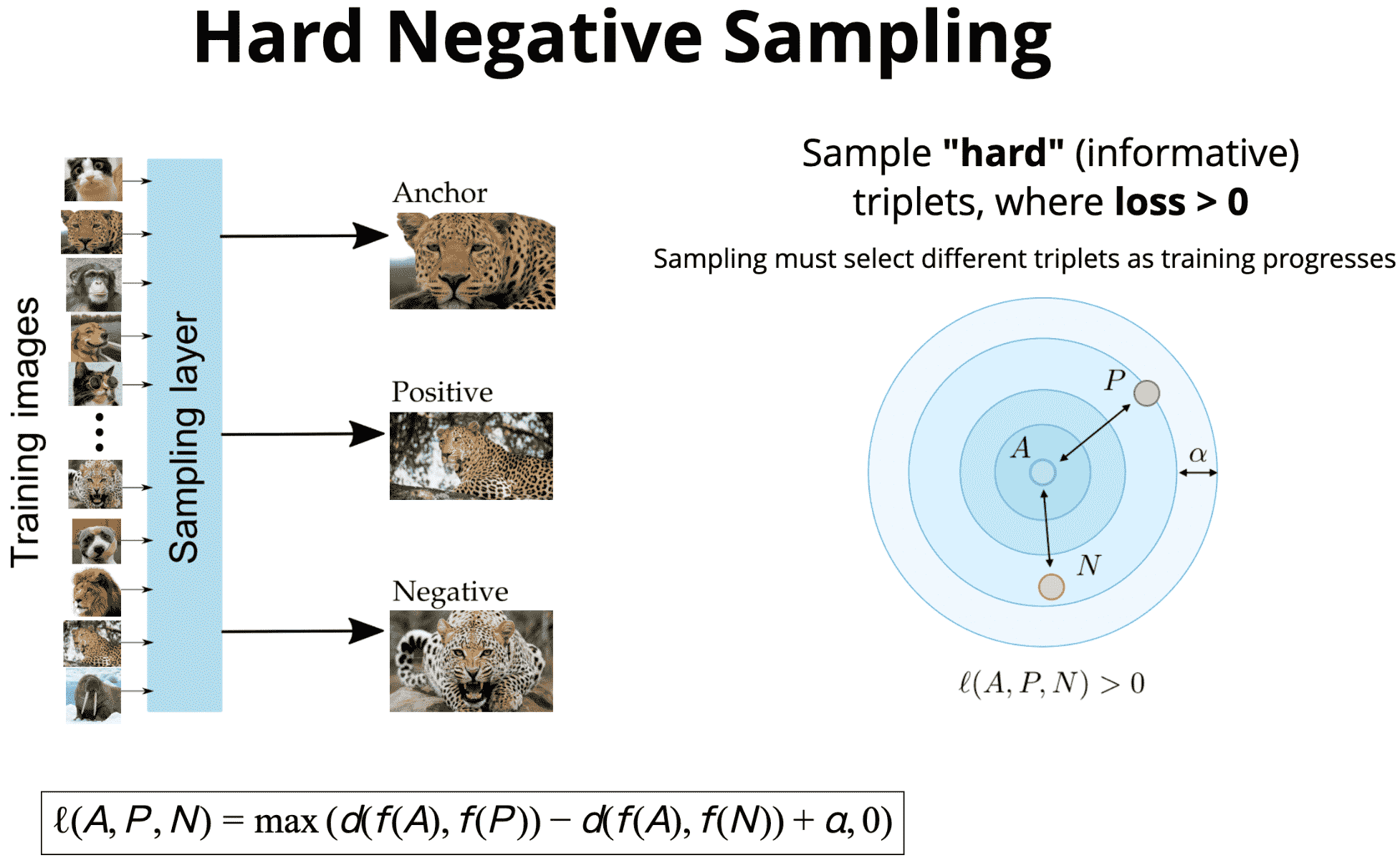
难样本采样,需要随着训练采样不同的三元组.

一种办法是,给定一个 anchor 图片 A,选择最难的正样本P(如,整个数据集中距离最远的同类样本);选择最难的负样本N(如,整个数据集中距离最近的不同类样本).
但其问题在于,对整个数据集计算最大距离和最小距离是不可行的(尤其是数据规模很大时). 此外,还可能会影响训练(因为错误标签的样本和离群样本都会影响难样本).
解决方案,在线生成三元组. 从每个 mini-batch(而不是整个数据集) 中选择每个 anchor A 的 P 和 N.
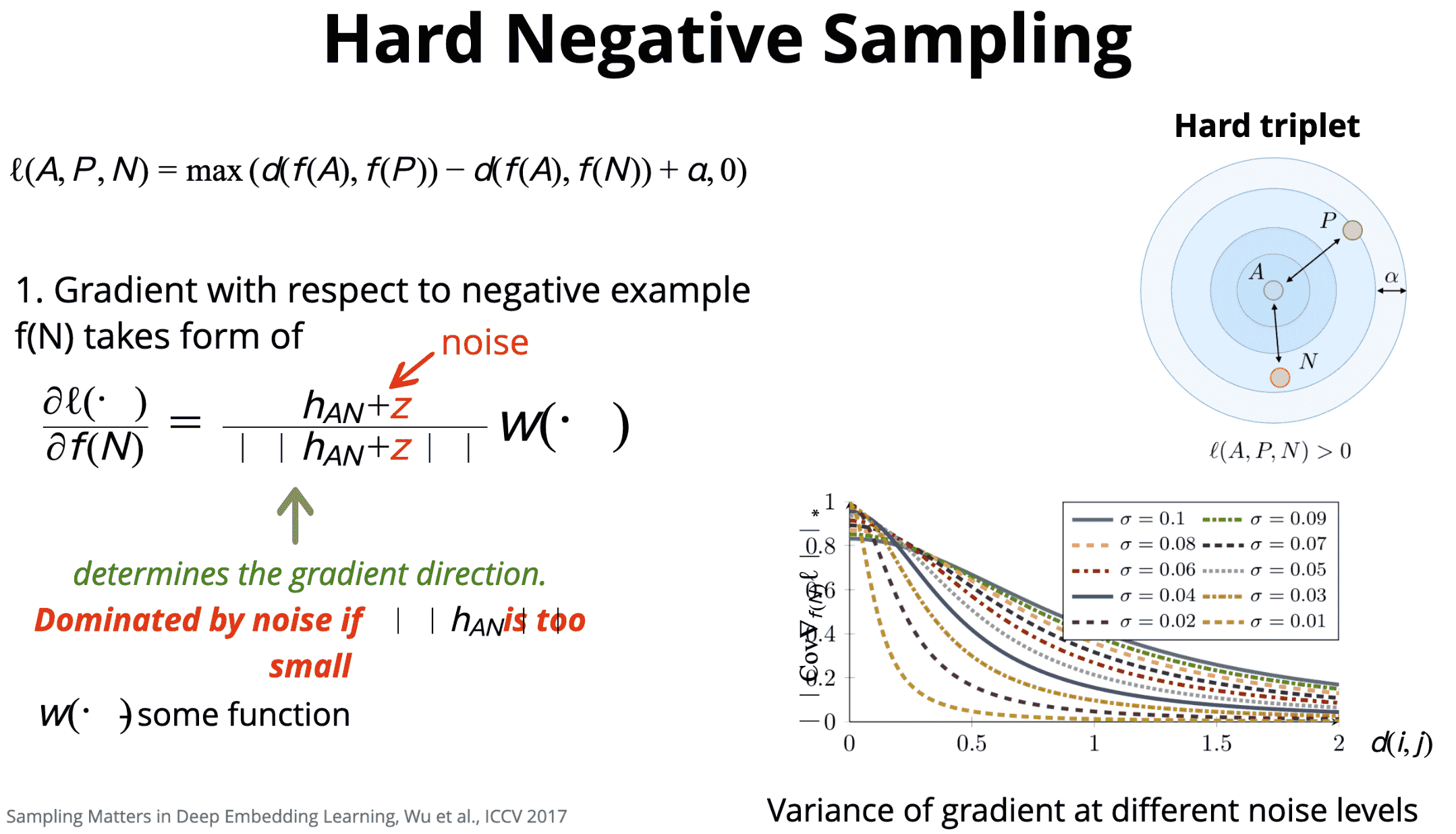
首先,计算损失函数关于负样本的梯度;

然后,选择最难的负样本,可能会导致在训练时过早陷入坏的局部最小点.
第二种方式是,半难负样本采样(Semi-hard Negative Sampling).
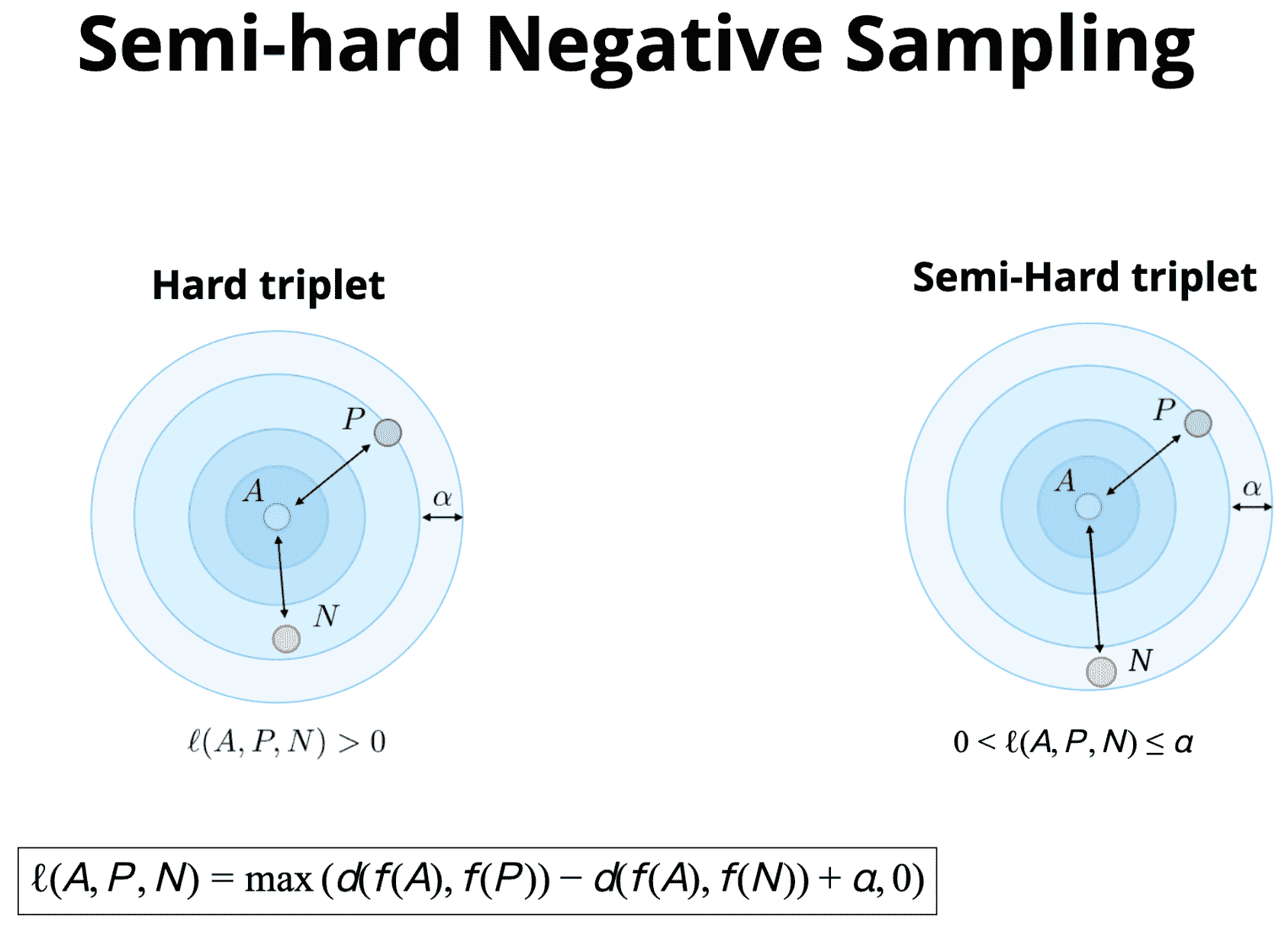
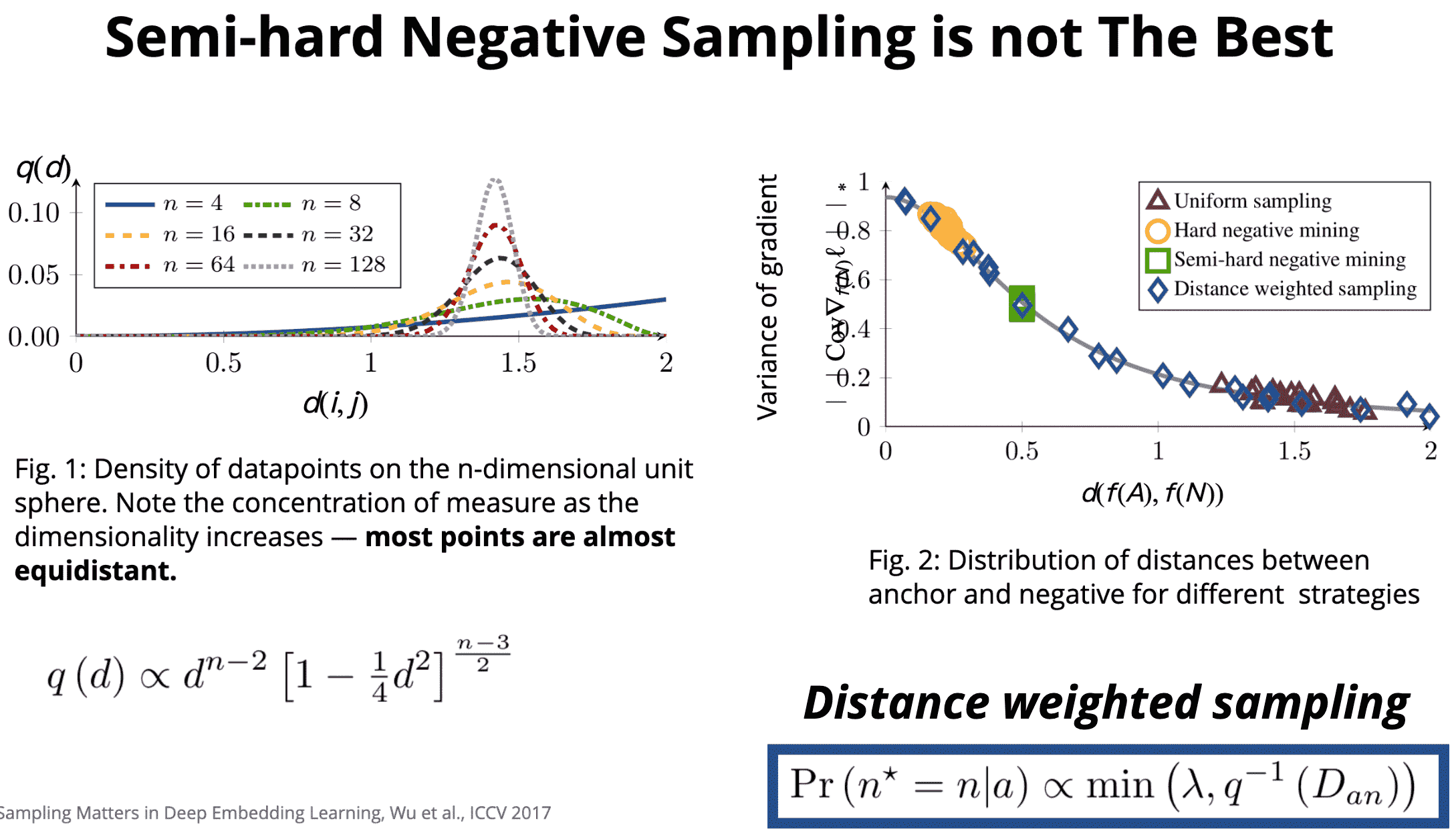
第三种方式是,采用MarginLoss.

3. 嵌入空间分而治之
3.1. 动机
动机1:DNN 的表征能力

通用逼近定理:在对激活函数的某种假设(mild assumptions)下,具有包含有限数据神经元的单个隐藏层的前向网络可以近似为紧凑子集R上的连续函数.
简单来说,可以采用 DNN 网络来逼近输入和输出之间的任何复杂关系.
可实际上,由于目标函数是高度非凸的,很难得到最优解. 往往会陷入局部最优.
动机2:数据分布是复杂且多模态的.

已有方法:对所有训练数据学习单个距离度量,其问题是过拟合和泛化能力弱.
解决办法:对于数据的非重复子集分别学习多个不同的距离度量.
3.2. 方法
[1] - 计算所有训练图片的特征向量;
[2] - 将特征数据划分为 K 个不同的数据子集;
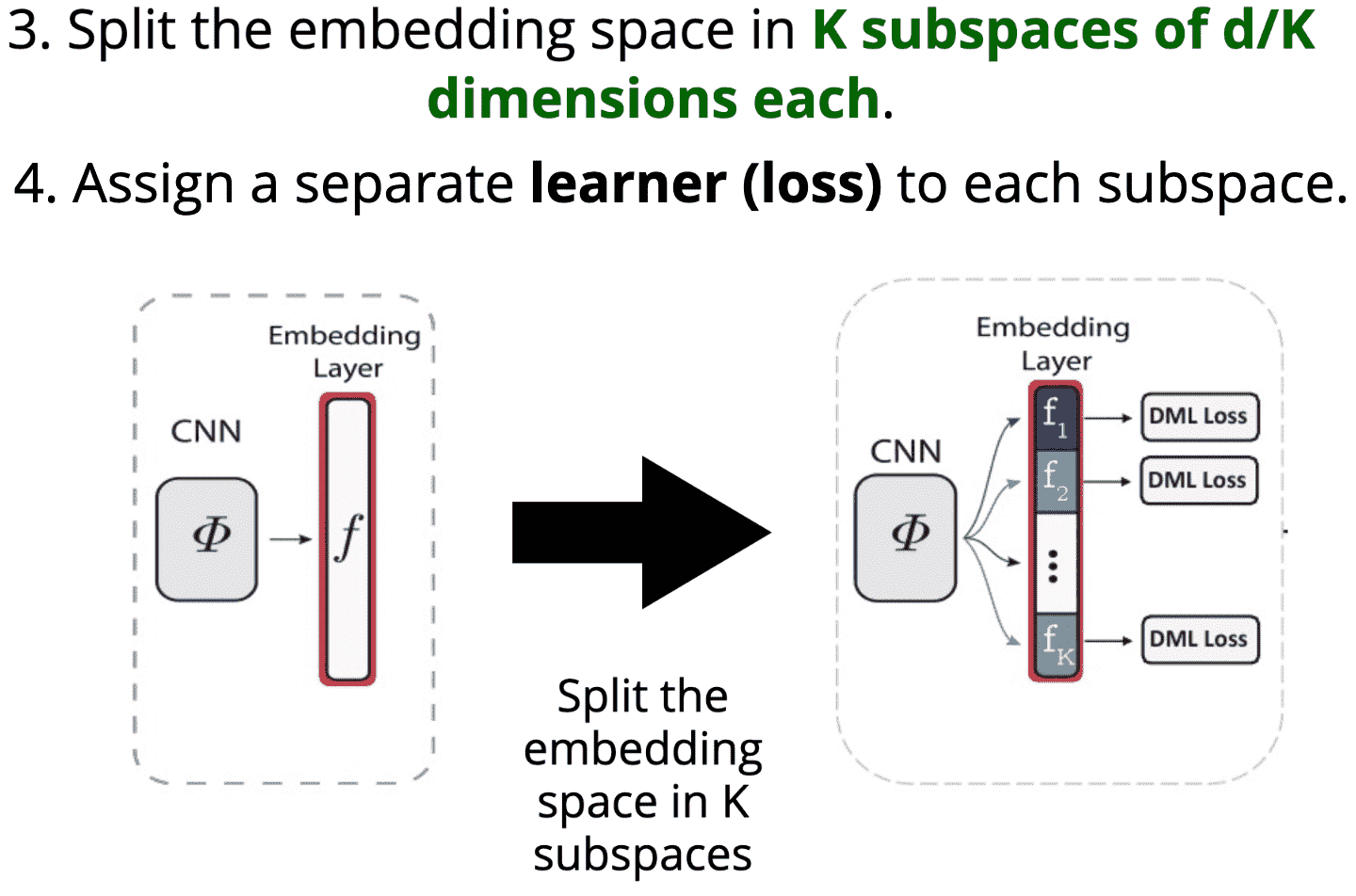
[3] - 将特征空间划分为 K 个子空间,每个子空间的维度为 d/K;
[4] - 每个子空间分别分配一个独立的学习器(不同的损失函数);
[5] - 采用 K 个学习器训练 K 个不同的距离度量;
[6] - 每 M 个 epochs 重复以上过程.

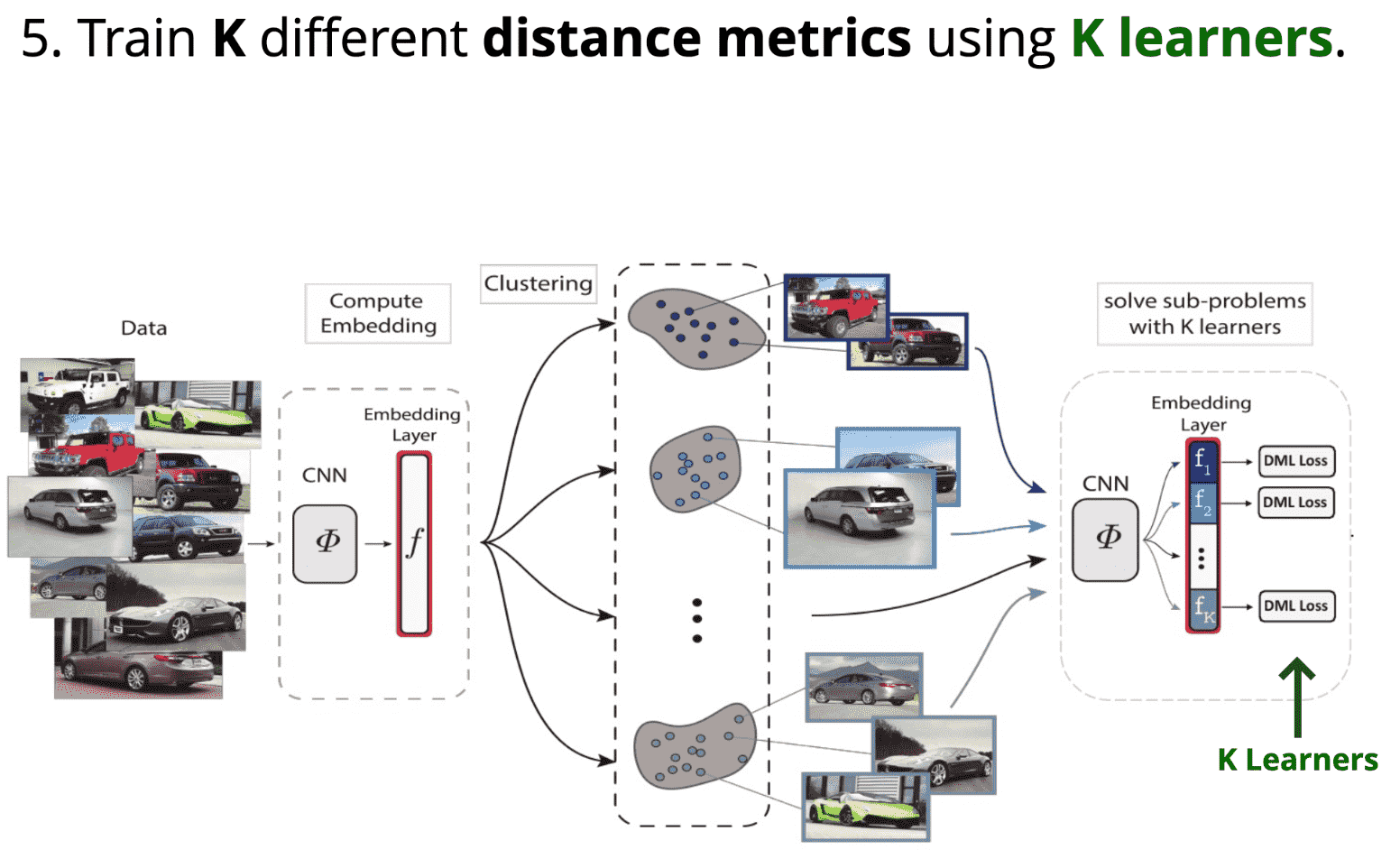
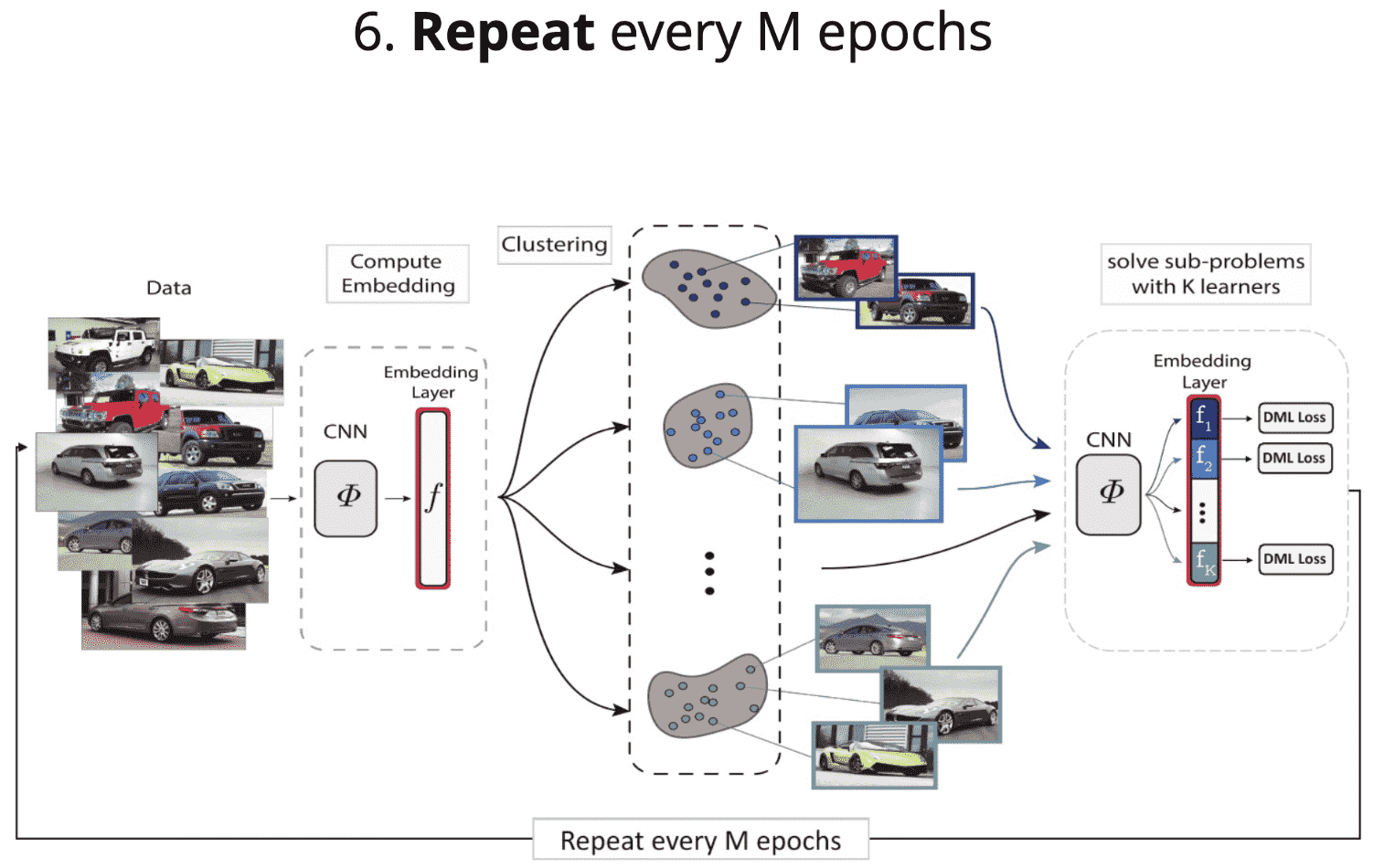
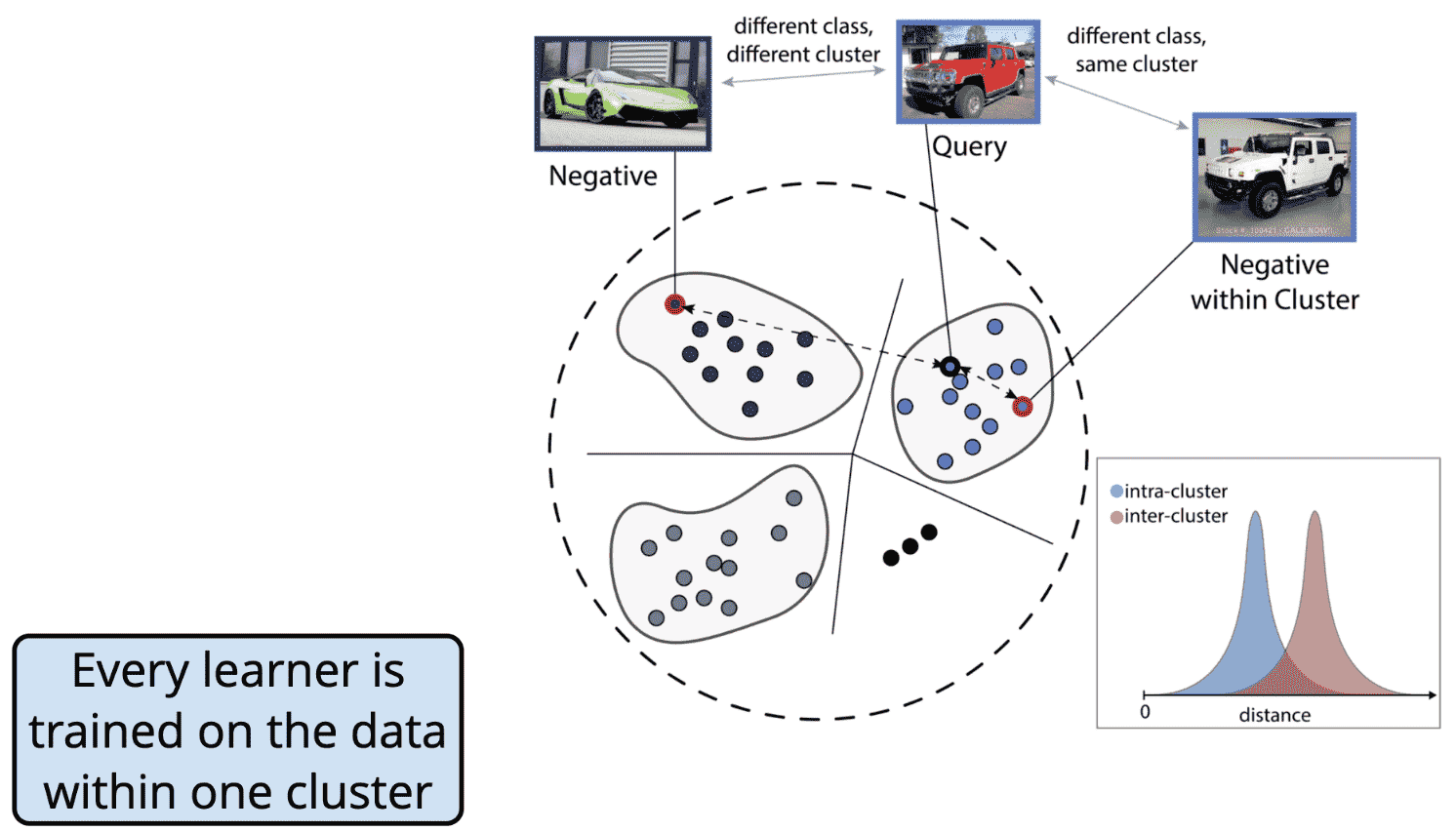
3.3. 难负样本挖掘
隐含的难负样本挖掘
每个学习器是对一个聚类的数据进行训练.