原文：Digging Deeper into Metric Learning with Loss Functions - 2019.11.12

作者：Jay Patel

深度度量学习网络(deep metric learning) 旨在将视觉相似图片投影到嵌入流形后彼此相邻，而视觉不相似图片相互分开.

学习得到的深度特征，具有很好的区分性，具有的特点是：类内方差小(差异性下)，类间方差大(差异性大). 该特征对于视觉搜索引擎至关重要.

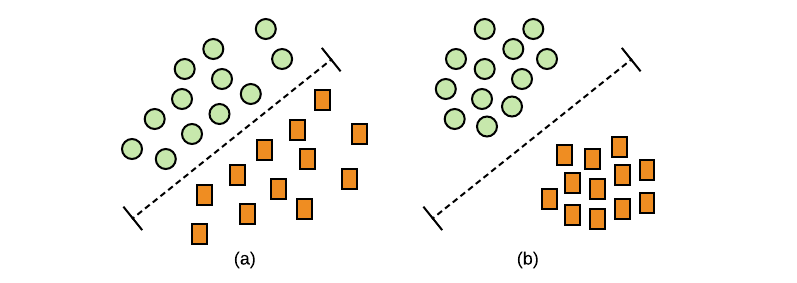
图：(a) 可分离性特征；(b) 可辨别性特征

此外，学习得到区分性特征后，深度网络模型能够很好的概括未曾学习过的产品图片，从而在嵌入空间中形成新的聚类簇.

深度度量学习网络的训练，类似于其他深度网络，区别在于，不同的损失函数显式的将相似图像在嵌入空间里聚集在一起，将不相似的图片彼此分离. 在训练过程中，将训练数据集图像输入网络，然后将其映射到嵌入空间. 使用损失函数来计算映射的损失，并采用适当的优化方法来调整网络权重. 在推理过程中，从嵌入层提取特征，并执行最近邻搜索来识别相似图像.

图：度量学习模型的训练和推断路线图示例.

这里汇总了度量学习中普遍使用的损失函数.

1. Contrastive Loss(对比损失)

为了最小化两张相似图片的特征之间的距离，最大化不相似图像的特征之间的距离，对比损失函数同时分别对相似性和不相似性进行计算.

对比损失函数直接计算两张相似图片的特征之间的距离，且考虑不相似图片的特征不能被一个距离间隔 $\alpha$ 分离时的距离.

对比损失函数公式定义如：

$$ L = \frac{1}{m} \sum _{(i,j)} ^{m/2} y_{i,j} D_{i,j}^2 + (1 - y_{i,j})[\alpha - D_{i, j}^2]^+ $$

这里，$m$ 为 mini-batch 内正样本对的数量(anchor-positive)

$D_{i,j} = ||f(x_i) - f(x_j)||^2$ 为图片$x_i$ 和 $x_j$ 的特征 $f(x_i)$ 和 $f(x_j)$ 之间的距离.

$y_{i,j} = +/-1$ 为指示器，如果 $(x_i, x_j)$ 是相似标签，则值为1，否则值为0.

$[.]^+$ 是 hinge 损失函数 $max(0, .)$.

每个特征向量对分别独立生成损失项，如图：

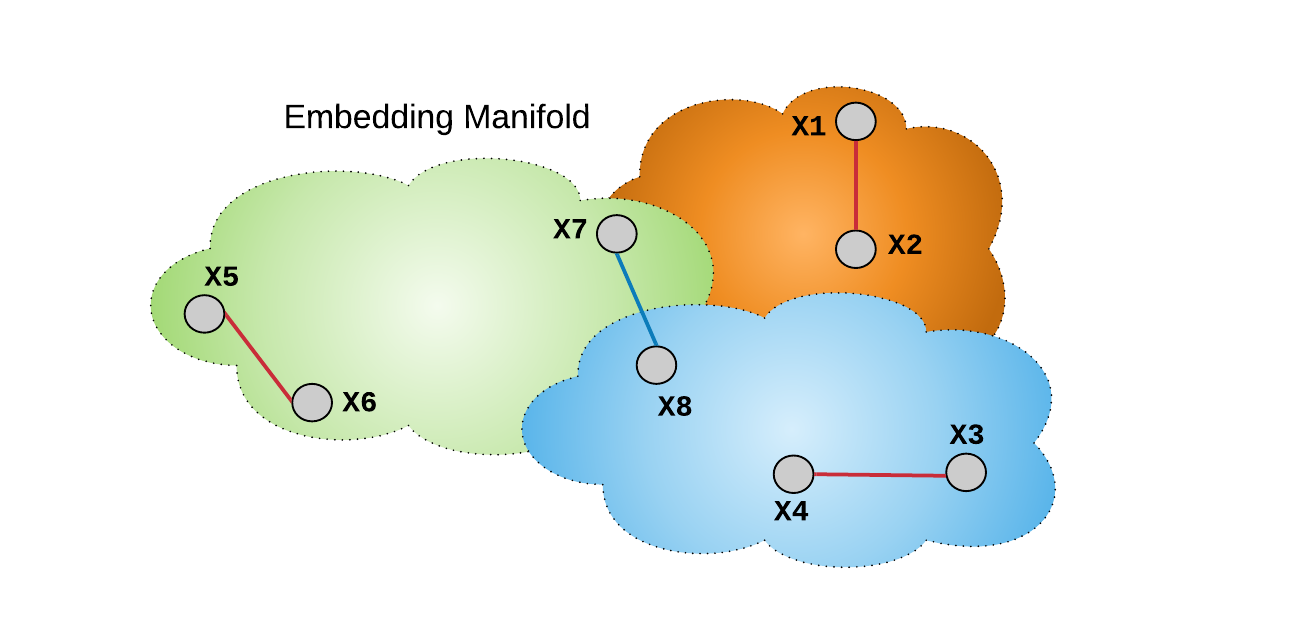
图：红色线表示相似标签的样本对，通过 $D_{i,j}$来作用于损失函数，其表示类内差异性. 蓝色线表示不同标签的样本对，通过 $\alpha - D_{i,j}$ 生成损失函数，其表示类间差异性.

对于数据集，样本数为 $N$，为了计算每次迭代的损失，需要进行 O(N^2) 次成对距离计算. 如果 mini-batch 为 B 的SGD优化，则计算量是 O(B^2).

然而，如果从数据集中随机选取 mini-batch，可能会导致 mini-batch 内没有任何正样本对，因此将不能优化类内差异性. 因此，每个 mini-batch 的正样本对数量的选择是很有必要的，最好接近 50% 的优化类内差异性，50% 的优化类间差异性.

例如，如果设置 mini-batch B=32，则，

[1] - 首先，随机选择 16 款产品；

[2] - 然后，从16款产品的每一款随机选择 2 张图片；

[3] - 则，在 mini-batch B=32时，生成得到了 16 个正样本对，15*16 个负样本对.

这种精心挑选 mini-batch 的处理，能够保证损失函数学习到类内差异性，而不增加额外的计算量.

尽管对比损失函数非常简单易理解，但，当设置距离间隔 $\alpha$ 时，并不能解决所有负样本对的视觉不相似性的程度. 例如，产品 A、产品B和产品C 的三张图片，如下图. 直观上，产品 A 和 产品 B 的视觉相似性比产品 A 和产品 C 的视觉相似性更高. 然而，当设置常数 $\alpha$ 时，当假设他们具有相似的视觉不相似性时，会将产品 B 和产品 C 的特征向量远离产品 A 的特征.

图：产品A和产品B是具有不同产品标签的视觉相似性；产品 C 是视觉上完全与产品A和产品B都不相同. 虽然具有不同尺度的视觉相似性，但 $\alpha$ 对于三款产品都是一个常数.

2. Triplet Loss(三元损失)

三元损失是度量学习中最常用的损失函数.

三元损失采用深度特征的三元组 $(x_{ia},x_{ip}, x_{in})$，其中，$(x_{ia}, x_{ip})$ 是具有相似产品标签的正样本对，$(x_{ia}, x_{in})$ 是不相似产品标签的负样本对.

网络训练的目标是，anchor $(x_{ia})$ 和正样本 positive $(x_{ip})$ 之间的距离 $D_{ia, ip}$ 小于 anchor $(x_{ia})$ 和负样本 negative $(x_{in})$ 之间的距离 $D_{ia, in}$，设定最小距离间隔 $\alpha$.

如图：

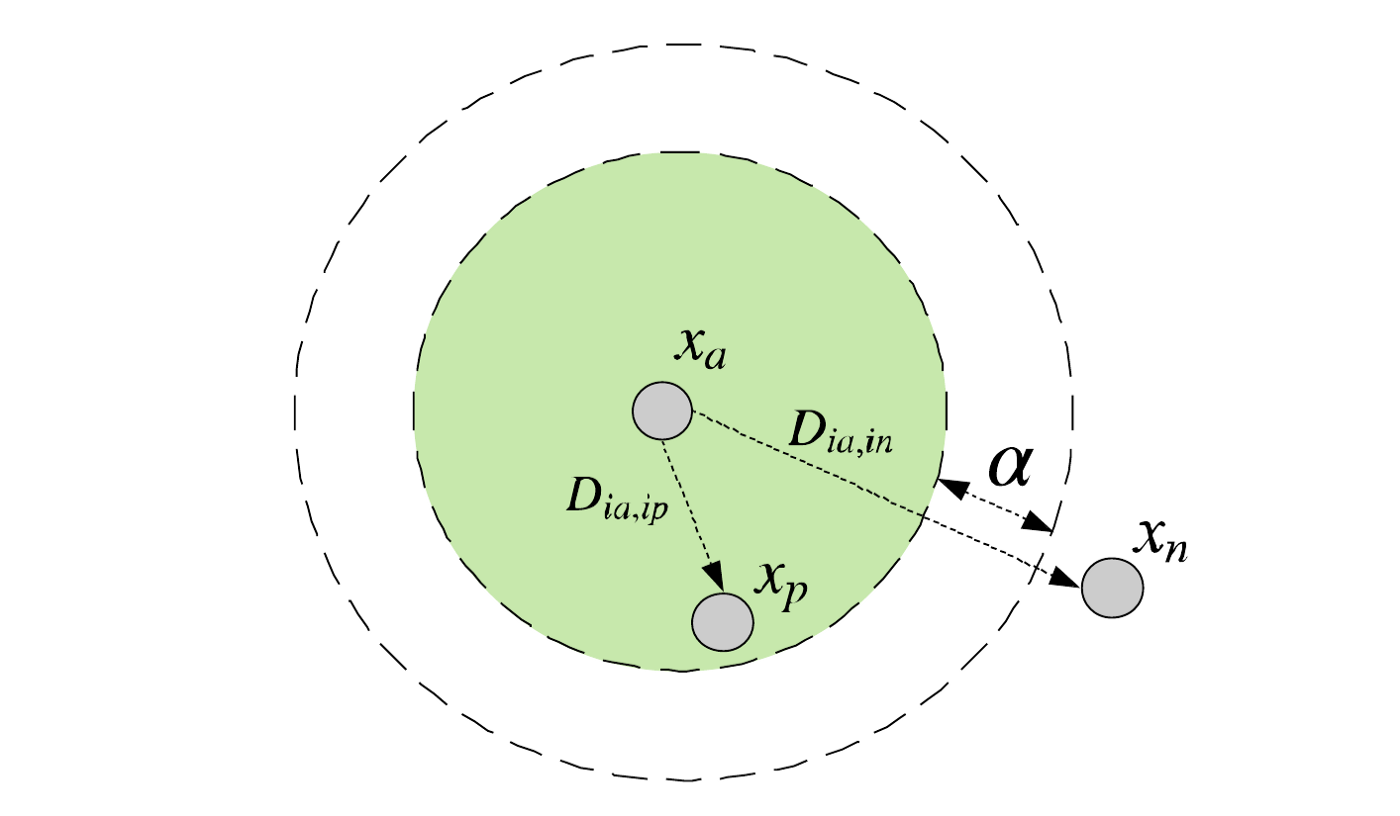
三元损失函数公式定义如：

$$ L = \frac{3}{2m} \sum_{i}^{m/3} [D_{ia, ip}^2 - D_{ia, in}^2 + \alpha]_+ $$

其中，$D_{ia, ip} = ||f(x_{ia}) - f(x_{ip})||_2$，$D_{ia, in} = ||f(x_{ia}) - f(x_{in})||_2$. 每个损失函数项分别考虑一个三元组，相对于预定义的 anchor 样本，以计算损失函数. 如图：

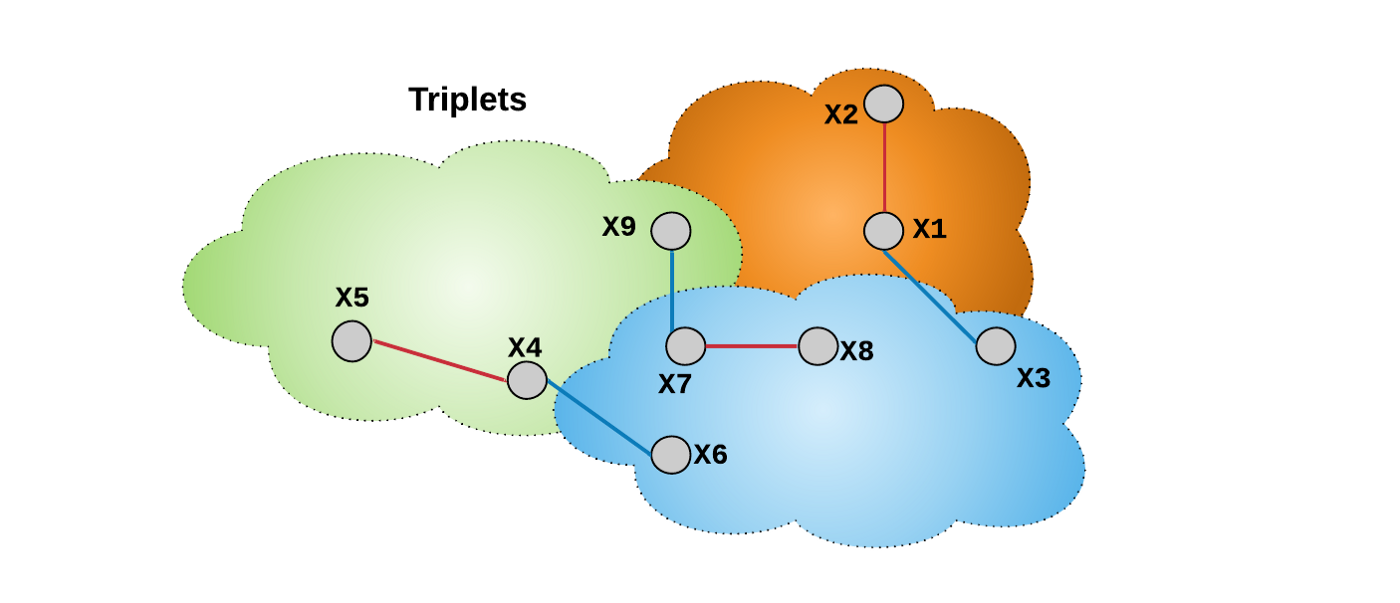
图：三元组 (X1, X2, X3)，红色线连接 anchor 样本 X1 和正样本 X2. 蓝色线连接 anchor 样本 X1 和负样本 X3. 与对比损失不同的是，三元损失的每个损失函数项同时处理类内差异性和类间差异性.

由于损失函数中 margin $\alpha$ 并不是直接根据两个嵌入特征之间的距离的，而是根据三元组内关于 anchor 的样本对间的相对距离，因此，相比于对比损失函数，三元损失函数可以将任意嵌入空间形变考虑在内.

尽管三元损失能够解决对比损失函数的问题，但其计算量是比较大的. 对于 minibatch B 个三元组的训练，需要计算minibatch 内所有可能的三元组之间的距离，其有超过 O(N^3) 组可能的三元组，对于大规模数据集的训练，其计算量是巨大的.

例如，数据集有 20 个不同的产品类，每个产品包含 15 张图片，可以从 15 张图片中选取 2 张，进行 20 次组合，共 ((15x14)/2)x20= 2100 个有效三元组(2100 个可能的 anchor-positive 样本对，每个从数据集中选择一个负样本). 计算损失函数时，其需要 2100/m (m 为 mini-batch 大小) 次迭代.

此外，随着训练的收敛，大多数三元组都满足正样本对和负样本对之间的距离 margin 约束.导致大部分三元组对损失函数贡献很小，使得学习缓慢，训练收敛缓慢.

对于训练慢的问题，一般采用基于 semi-hard 和 hard 负样本挖掘的训练策略.

3. Lifted Structure Loss

当采用三元损失作为目标函数进行模型训练时，其并不能充分利用 mini-batch 内的样本信息，主要是因为给定 anchor 样本的正样本和负样本是预先定义的.

Lifted structure loss 的思想是，采用所有的 O(B^2) 样本对，而不是 O(B) 个独立的样本对，来提升 mini-batch 的优化. 如图：

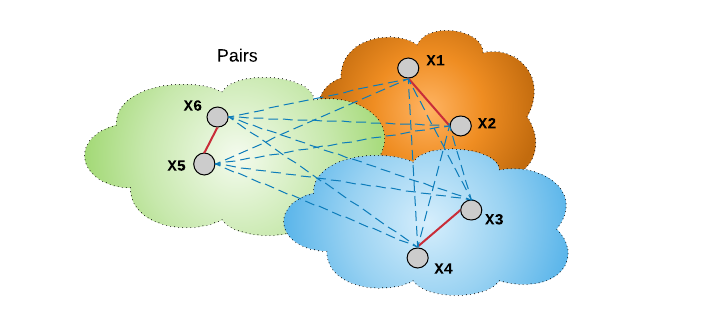
图：anchor 和正样本对 (X1, X2)，以及mini-batch 内的其余样本对的连接.

Lifted structure loss 中，样本对的节点是分别与 mini-batch 内所有负样本节点进行连接的. 与三元损失函数不同之处是，其不需要通过预定义 anchor 来定义负样本，而忽略了 mini-batch 内所有的其他可用的负样本. Lifted structure loss 将每个正样本看作是一个 anchor，并寻找其负样本，以计算损失函数. 其有助于网络训练的速度更快，收敛性更好.

需要特别注意的是，从 mini-batch 样本中随机徐娜则负样本，例如图中的给定样本对 X1和X2，其并没有和 hard 负样本一样，推动网络的快速收敛. 为了提升收敛速度，作者建议，对于给定样本对的每个样本分别挖掘其 hard 负样本，如下图：

图：蓝色实线表示 X1 和 X2 的 hard 负样本. 尽管 X1 将 X6 考虑为负样本，其仍与 mini-batch 内的所有负样本连接.

Lifted struceture loss 函数最小化平滑上界，以稳定网络训练. 具体来说，其定义如：

$$ L_{i,j} = log(\sum_{(i, k) \in N} e^{(\alpha - D_{i,k})} + \sum_{(i, l) \in N}e^{(\alpha - D_{j, l})} ) + D_{i,j} $$

$$ L = \frac{1}{2|P|} \sum_{(i, j) \in P} max(0, L_{i,j})^2 $$

其中，$D_{i,j} = ||f(x_i) - f(x_j)||_2$.

$P$ 和 $N$ 分别表示 mini-batch 内所有的正样本对和负样本对.

4. N-Pair Loss

Multi-class N-pair loss 类似于 Lifted Structure loss，其在计算 mini-batch 的损失函数值时利用了多个负样本，且并不像三元损失和对比损失一样收敛速度变慢. 如图.

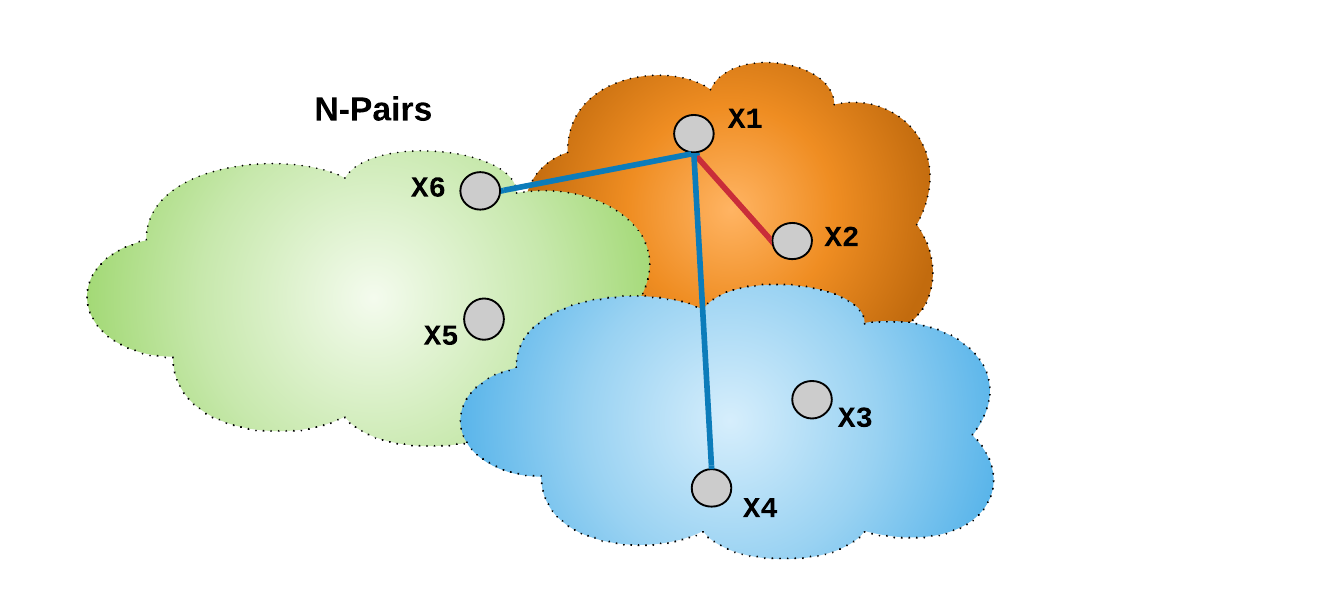
图：对于损失函数 L 中的每一项，给定样本对 (X1, X2) 中的 anchor 样本 X1 利用了 mini-batch 内的 N-1 个负样本(图中是 X4和 X6)，其中，N 是mini-batch 内样本对数.

采用 N 个样本对计算损失函数的公式如：

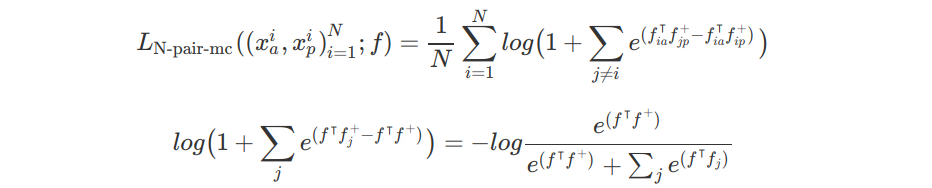
其中，$N$ 为相似标签的图片对的数量.

假设，$f$ 为特征向量，$f^+$ 为权重向量，公式右边的分母作为似然函数 $P(y=y+)$.

上述公式类似于 multi-class logistic loss(如，softmax loss).

此外，N-pair loss 函数对于训练数据集包含大量的产品标签时，效果更优. 不同样本对的数量 N 的值越大，则逼近的精度越高.

N-pair loss 相比于 Lifted Structure loss 的一个优势在于，其尝试以概率方式计算正样本对和负样本对的余弦(cos)相似性. 换句话说，N-pair loss 计算一对特征之间的余弦相似性，采用 mini-batch 的成对比较，提升属于相同标签的特征的概率. 由于余弦相似性度量(即概率) 具有尺度不变形，如下图，N-pair loss 在训练时具有对特征变化的鲁棒性.

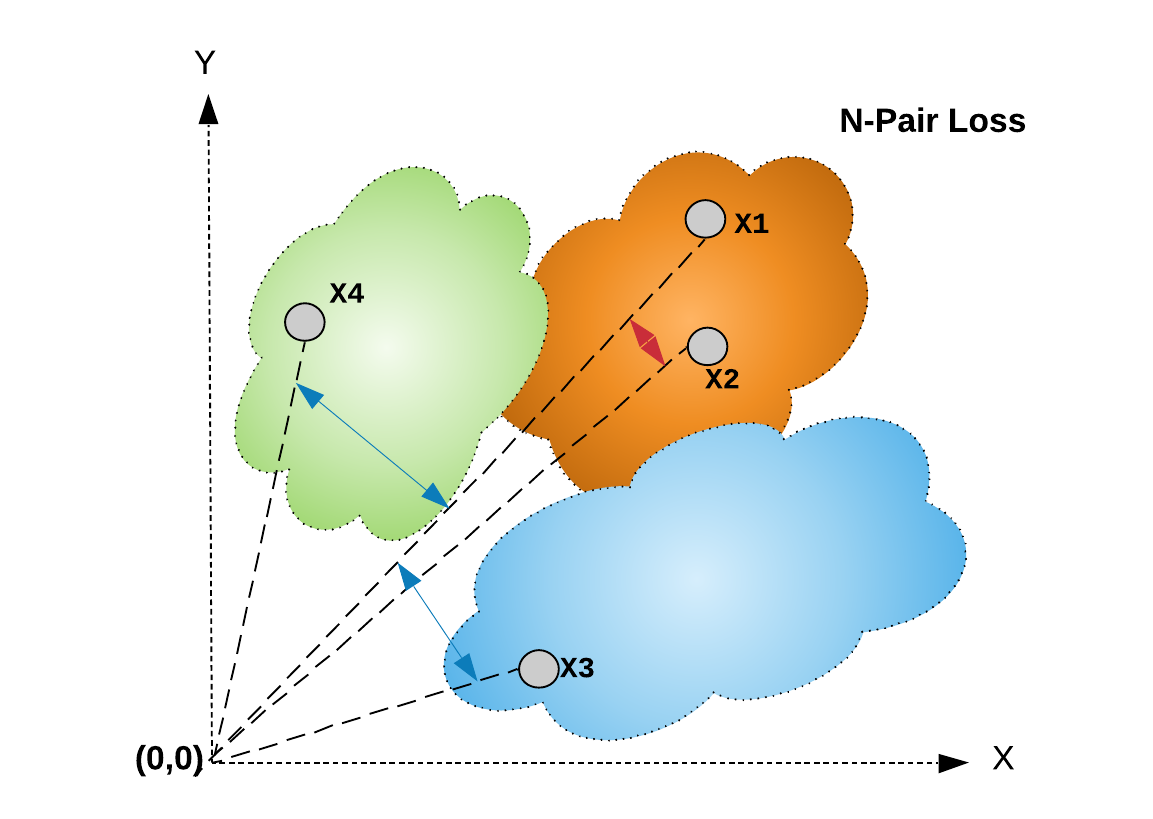
图：N-pair loss 直接计算 anchor X1 和正样本 X2 之间的余弦相似性，并以概率方式比较其和正样本和其余负样本之间的相似性.

5. Angular Loss

相比于上面提到的度量学习方法，主要是关注于优化绝对距离(对比损失)，或相对距离(三元损失、Lifted Structure Loss、N-Pair loss)，Angular loss提出根据三元三角内的关于负样本边的角度的三阶关系进行编码(Angular loss proposes to encode a third-order relation inside the triplet triangle in terms of an angle at the negative edge).

类似于 N-pair loss，Angular loss 通过定义角度距离(余弦距离)的损失函数，具有尺度不变形. 其将负样本特征向量拉离正样本聚类，将正样本特征向量推向彼此，如图：

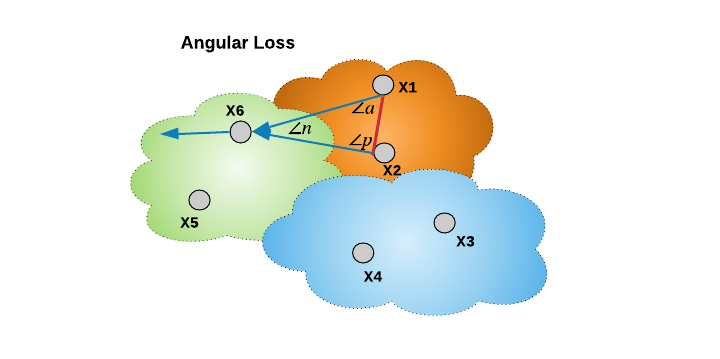
Angular loss 的几个有点在于：

[1] - 不同于欧式距离，角度距离(余弦距离) 是平移不变相似性度量. 当考虑几何角度时，不仅受益于尺度不变性，还引入了旋转不变性. 即使在训练时，图像特征尺度变化比较频繁，对于固定的 margin $\alpha$，$\ang n \le \alpha$ 往往是满足的. 简而言之，损失函数中的几何角度视角对于特征图的局部变化更加鲁棒.

[2] - 余弦规则解释了 $\ang n$ 的计算需要三元组的所有三个边. 而原来的三元组仅考虑了两个边. 新增的约束有利于优化的鲁棒性和有效性.

[3] - 当采用欧式距离时，对于损失函数来说，损失margin m 的选择不是一项直观的任务. 主要是因为，随着数据集大小的增长，目标标签的类内变化会比较大. 该超参数的调参至关重要. 相比而言，由于其尺度不变性，设置 $\alpha$ 就简单很多.

此外，angular loss 易于与传统度量学习损失函数相结合，以提升整体表现. 例如：

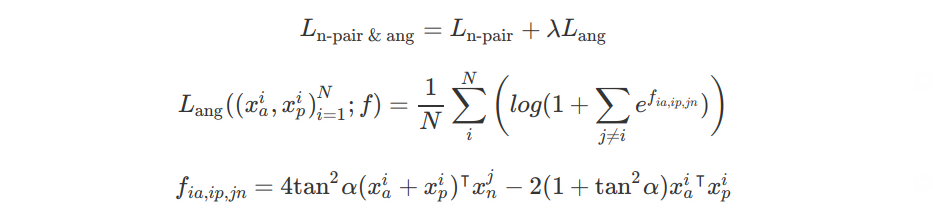
其中，$\lambda$ 是 N-pair loss 和 angular loss 的权重参数. 默认 $\lambda =2$，$\alpha$ 一般设置为 35-60 度.

6. Divergence Loss

尽管上述度量学习目标函数，可以将给定图像映射到嵌入流形里，但他们并不一定能顾及到相同图片的各个方面. Divergence loss 通过不同的组合模块来探索这一方面.

Divergence loss 是一个正则项，可以将其添加到度量学习损失函数，以联合监督. 其增加不同组合模块学习到的图像特征之间的距离. 换句话说，其鼓励每个模块去学习输入图像的不同属性，公式如，

$$ L(x_i, y_i) = \sum_m L_{1, (m)} (x_i, y_i) + \lambda L_2(x_i) $$

其中，$(x_i, y_i)$ 是所有训练样本和标签的集合. $L_1$ 是第 m 个模块的度量学习损失函数，$L_2$ 是每个模块 m 的特征嵌入多样性的正则项. $\lambda$ 是权重参数，以控制不同的正则子.

$$ L_2(x) = \sum_i \sum_{a, p} [m - D_{ia, ip}^2]_+ $$

其中，$x_i$ 是对应于图像 $x$ 的特征向量. $D_{ia, ip}$ 表示两个不同的学习模块 $a$ 和 $p$ 得到的图像特征向量之间的距离. $m$ 是 divergence loss 的 margin，一般设为 1. $[.]^+$ 表示 hinge 函数 $max(0, .)$.

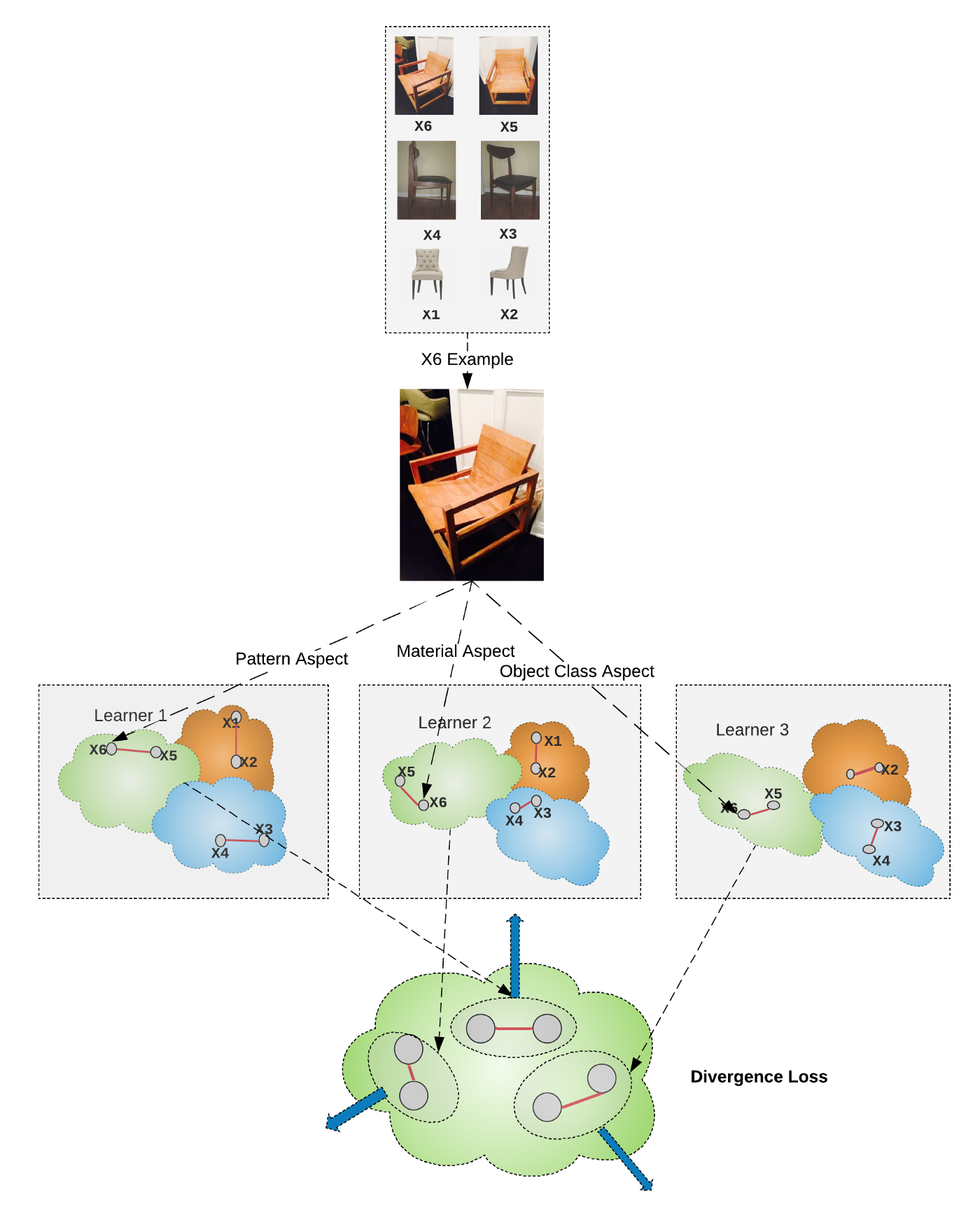
图：Divergence loss 将不同学习子模块的特征向量互相拉远. 换句话说，其鼓励通过不同学习子模块得到的特征向量，关注于啊图像的不同部分(图中 X6). 这样就可以得到多个学习子模块的多样性嵌入空间. 每个学习子分别满足将相似标签在嵌入空间临近的相似性约束.

7. 总结

这里简单汇总讨论了度量学习损失函数，其在深度度量学习网络训练中具有至关重要的作用.

然而，尽管基于这些损失函数的网络已经在视觉搜索中取得了很大成功，但深度度量学习网络的训练是计算量非常大且耗时的. 如，对于大小为 N 的数据集，梯度计算量为 O(N^2) 或 O(N^3)，因此需要梯度下降中，需要严格限制 mini-batch (B). 其可以将计算量降低到 O(B^2) 或 O(B^3)，不过，如何选取 mini-batch 将会非常重要.

SGD 计算时，通过随机采样数据集和适当的 batchsize 来构建 minibatch. 然而， 例如，如果在三元损失函数中，采用随机采样来构建 mini-batches，很有可能在最后没有任何正样本对或负样本对，导致其梯度非常小. 因此，在 mini-batch 梯度处理中，虽然可以通过 mini-batch 降低计算量，但是如果 mini-batches 的损失贡献小，则有可能需要更多计算量，以达到最优的点. 因此，训练数据集的采样和minibatch的构建策略，使其能够对损失函数包含充分的信息，而又不要太大，对于加快度量学习网络的训练至关重要.

参考

[1] Hadsell, R., Chopra, S., & LeCun, Y. (2006, June). Dimensionality reduction by learning an invariant mapping. In 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06) (Vol. 2, pp. 1735–1742). IEEE.

[2] Wen, Y., Zhang, K., Li, Z., & Qiao, Y. (2016, October). A discriminative feature learning approach for deep face recognition. In European conference on computer vision (pp. 499–515). Springer, Cham.

[3] Schroff, F., Kalenichenko, D., & Philbin, J. (2015). Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 815–823).

[4] Oh Song, H., Xiang, Y., Jegelka, S., & Savarese, S. (2016). Deep metric learning via lifted structured feature embedding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 4004–4012).

[5] Sohn, K. (2016). Improved deep metric learning with multi-class n-pair loss objective. In Advances in Neural Information Processing Systems (pp. 1857–1865).

[6] Wang, J., Zhou, F., Wen, S., Liu, X., & Lin, Y. (2017). Deep metric learning with angular loss. In Proceedings of the IEEE International Conference on Computer Vision (pp. 2593–2601).

[7] Kim, W., Goyal, B., Chawla, K., Lee, J., & Kwon, K. (2018). Attention-based ensemble for deep metric learning. In Proceedings of the European Conference on Computer Vision (ECCV) (pp. 736–751).