论文:Multi-Similarity Loss with General Pair Weighting for Deep Metric Learning - CVPR2019
Github: msight-tech/research-ms-loss
团队:码隆科技
参考:Muti-Similarity Loss:考虑了batch中整体距离分布的对比损失函数 - 2020.09.25
出处:AI公园 - 微信公众号
度量学习的目标是学习到一个特征空间,使得相似样本的特征向量拉近,而不同样本的特征向量推远.
论文提出的 Multi-Similarity Loss(MS Loss),通过两步迭代 - 挖掘(mining)和加权(weighting),更全面的考虑了成对权重(pair weighting)的三方面的相似性 - 样本对的自相似性、负样本对的相似性、正样本对的相似性,以更好采集和加权样本信息对.
1. MS Loss
如图:
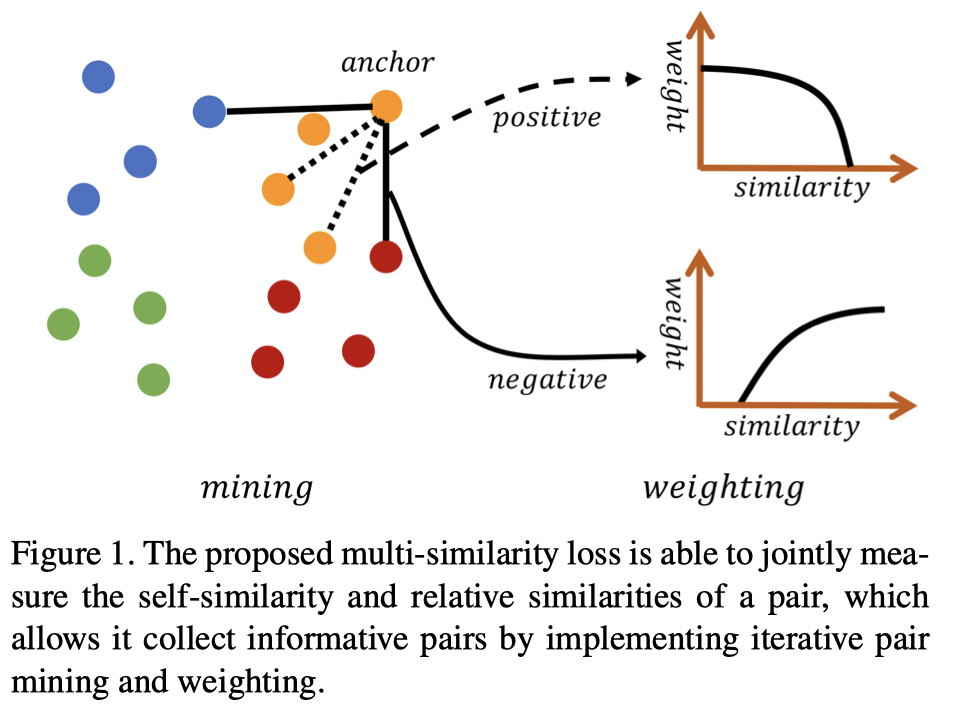
图1. MS loss 能够联合度量样本对的自相似性和相对相似性,使得其可以通过迭代的挖掘和加权来得到信息度更高的样本对.
MS Loss 定义:
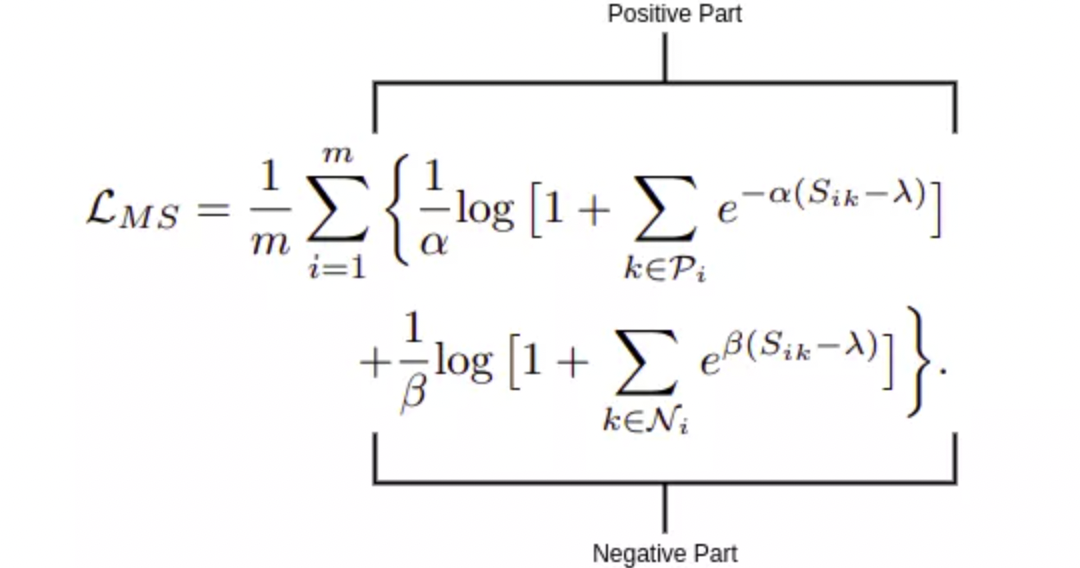
其中,$S_{ik}$ - 样本对的余弦相似性,$\lambda$ - 相似度margin,$\alpha,\beta$ 超参数.
MS Loss 包含两部分:正样本部分和负样本部分.
1.1. 正样本部分
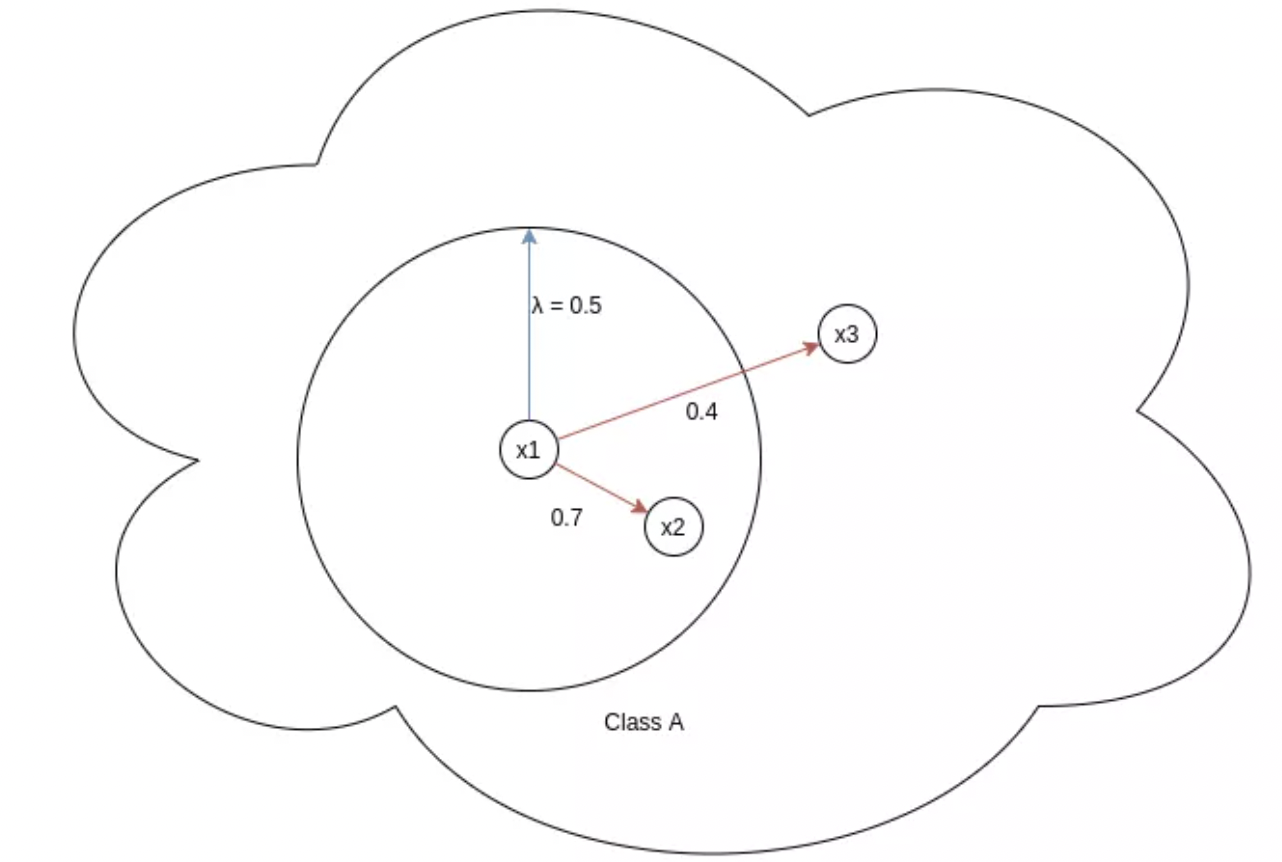
图:x1 = Anchor, x2,x3 = positives, λ = margin
这部分只考虑正样本对. $\lambda$ 表示相似度的 margin,控制了正样本对的紧密程度. 对于相似度小于 $\lambda$ 的正样本对进行惩罚.
如上图,两个样本对 (x1, x2) 和 (x1, x3),正样本对(x1, x2) 的损失很低,因为 $e^{(- \alpha (S_{ik} - \lambda))} = e ^{(- \alpha (0.7 - 0.5))} = e^{(-0.2 \alpha)}$. 而正样本对 (x1, x3) 的损失为 $e^{(- \alpha (S_{ik} - \lambda))} = e ^{(- \alpha (0.4 - 0.5))} = e^{(0.1 \alpha)}$. 由于超参数 $\alpha$ 是大于零的,则正样本对(x1, x2) 的损失相比于 (x1, x3) 的值是非常小的.
1.2. 负样本部分

图: x1 = anchor, x2,x3 = negatives, λ = margin
这部分只考虑负样本对,确保负样本与 anchor 的相似性尽可能的低. 即,靠近 x1 的样本对(即具有高相似性),应该比远离 x1 的样本(即具有较低的相似性) 受到更大的惩罚.
如图,样本对 (x1, x2) 的损失为 $e^{(- \beta (S_{ik} - \lambda))} = e ^{(- \beta (0.3 - 0.5))} = e^{(-0.2 \beta)}$,样本对 (x1, x3) 的损失为 $e^{(- \beta (S_{ik} - \lambda))} = e ^{(- \beta (0.1 - 0.5))} = e^{(-0.4 \alpha)}$.
2. 样本对相似性
在计算成对样本相似性时,一般采用余弦距离或欧式距离等.
这里,以一个负样本对(negative pair) 为例,说明三种类型的相似性(正样本对相似性同理).
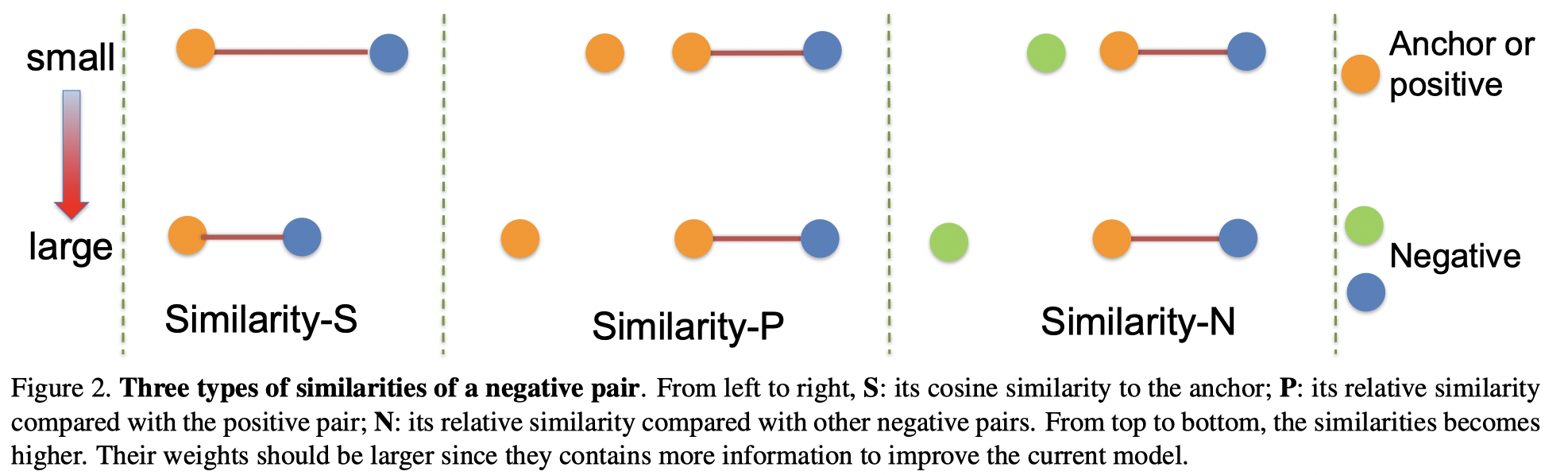
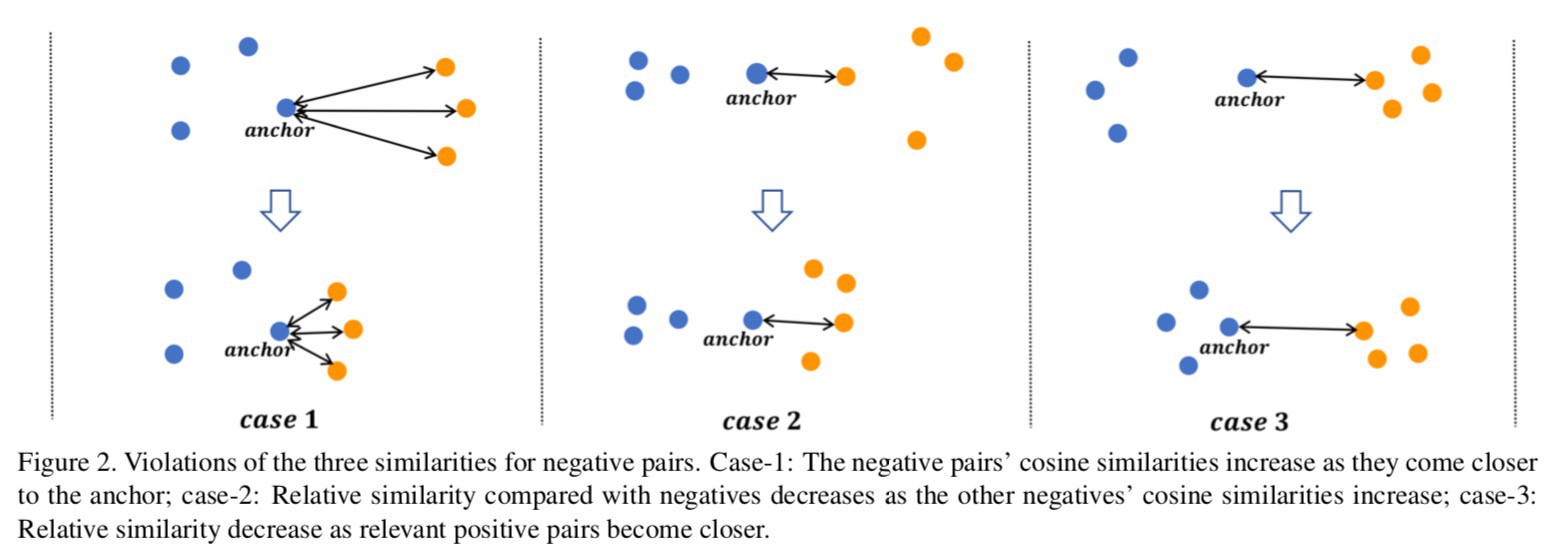
对于每一个样本对,不仅需要考虑样本对本身的自相似性,同时还要考虑它与其它样本对的相对相似性. 其中相对相似性又可以分为正相对相似性 (正样本)、负相对相似性(负样本)两种相似性.
[1] - 自相似性:根据样本对自身计算出的相似性,这是一种最常用也是最重要的相似性. 例如,当一个负样本对的余弦相似性较大时,意味着很难把该样本对所对应的两种类别区分开来,这样的样本对对模型来说是困难的,也是有信息量的,对于模型学习更有区分度的特征很有帮助. 另一方面,自相似性很难完整地描述embedding空间的样本分布情况.
[2] - 正相对相似性:不仅考虑当前样本对自身的相似性,还考虑局部邻域内正样本对之间的相对关系.
[3] - 负相对相似性:不仅考虑当前样本对自身的相似性,还考虑局部邻域内负样本对之间的相对关系.
2.1. 自相似性(Similarity-S)
自相似性(Self-similarity)定义为,负样本和 anchor 样本之间的余弦距离.
如果负样本对具有较高的自相似性,则意味着,更难区分来自不同类别的两对样本. 该样本对被标记为难负样本对(hard negative pairs),其对于区分性特征的学习具有更高的价值.
如图:
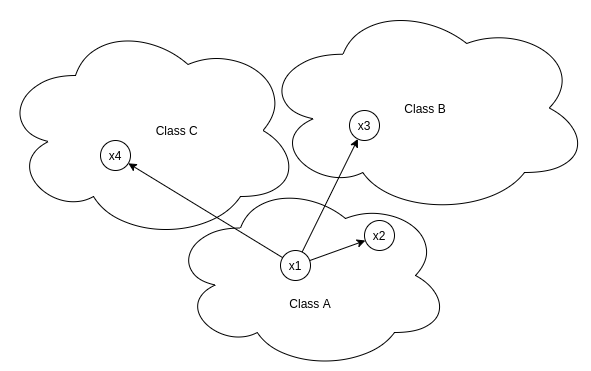
图:x1-anchor,x-positive,x3,x3-negatives
自相似性确保属于正类的样本距离 anchor 的距离比属于负类的样本距离 anchor 的距离更近.
2.2. 负样本相对相似性(Similarity-N)
负样本相对相似性(Negative relative similarity) 衡量的是其自身相似性和其他负样本对相似性之间的差异性.
图2(右),当负样本自相似性保持固定时,负样本对的 Similarity-N 值变大.
明显的,当 Similerity-N 变大时,相比于其他负样本,该样本对包含更多有价值的信息.
对于负样本对 (x1, x2),不仅根据 (x1, x2) 之间的自相似性,还根据其相对相似度,即,batch 内的其他对 x1 的负样本来分配权重,权重分配公式为:
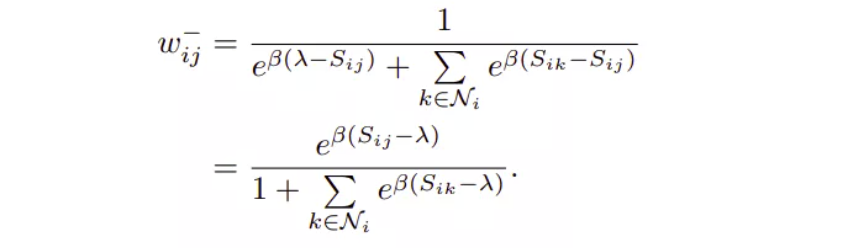
样本对权重 $w_{ij}$ 被定义为该样本对的损失相对于总损失的贡献.
结合图示:

其中,$S_{ij}$ 对应 (x1, x2) 的自相似性,$S_{ik}$ 对应 (x1, x3)、(x1,x4)、(x1, x5)、(x1- x6)、(x1, x7) 之间的负样本相似性.
图中,虽然 (x1, x2) 在所有负样本 case 中,具有相同的 $S_{ij}$,但其权重 $w_{ij}$ 在不同的 case 中是不一样的.
[1] - Case1 - 所有其他负样本相对于 x1 的距离比 x2 与 x1 的距离更远.
[2] - Case2 - 所有其他负样本相对于 x1 的距离和 x2 与 x1 的距离一样.
[3] - Case3 - 所有其他负样本相对于 x1 的距离比 x2 与 x1 的距离更近.
在三种 Case 中,$w_{ij}$ 的区分在于分母项 $\sum e^{(\beta(S_{ik} - S_{ij}))}$. 其中,$S_{ik}$ 对应 (x1, x3)、(x1,x4)、(x1, x5)、(x1- x6)、(x1, x7) 之间的余弦相似性,$S_{ij}$ 对应 (x1, x2) 的余弦相似度.
[1] - Case1 - $w_{ij}$ 最大,因为 $\sum e^{(\beta(S_{ik} - S_{ij}))}$ 最小,$S_{ik} < S_{ij}$,使得指数为负数.
[2] - Case2 - $ w_{ij} $ 中等,因为 $\sum e^{(\beta(S_{ik} - S_{ij}))}$ 指数为 0.
[3] - Case3 - $w_{ij}$ 最小,因为 $\sum e^{(\beta(S_{ik} - S_{ij}))}$ 最大,$S_{ik} > S_{ij}$,使得指数为正数.
2.3. 正样本相对相似性(Similarity-P)
正样本相对相似性(Positive relative similarity) 的计算是考虑了正样本对的关系. 其定义为,其自身余弦相似性和其它正样本对的余弦相似性的差异.
如图2(中),随着正样本的变远,Similarity-P 增加.
明显的,这种情况是,负样本比正样本更接近 anchor,正确检索出 anchor 的对的样本是比较有挑战.
因此,负样本应该被指定更高的权重.
对于正样本对的权重分配公式为:
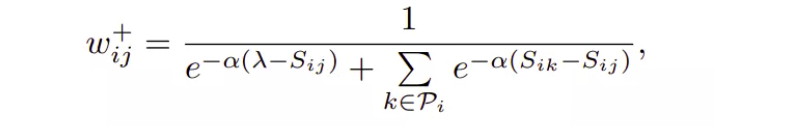
结合图示:

其中,$S_{ij}$ 对应 (x1, x2) 的自相似性,$S_{ik}$ 对应 (x1, x3)、(x1,x4)、(x1, x5)、(x1- x6) 之间的正样本相对相似性.
负样本相对相似性表示单个负样本对与batch中所有其他负样本对的关系. 类似地,正样本相对相似性定义了batch中单个正样本对(x1-x2)与所有其它所有正样本对(x1-x3、x1-x4、x1-x5、x1-x6)之间的关系.
按照在负样本相对相似性下所做分析,可以很容易地验证上图所示的结果.
2.4. 不同损失函数的相似性类型

3. 难样本挖掘
难样本挖掘,包括困难正样本和困难负样本的挖掘.
MS Loss 的作者在训练时仅使用了困难的负样本和正样本,并丢弃了其他的样本对,因为它们对效果提升几乎没有贡献,同时还降低了性能,只选择了那些具有更多价值信息的样本对,也使得算法计算速度更快.
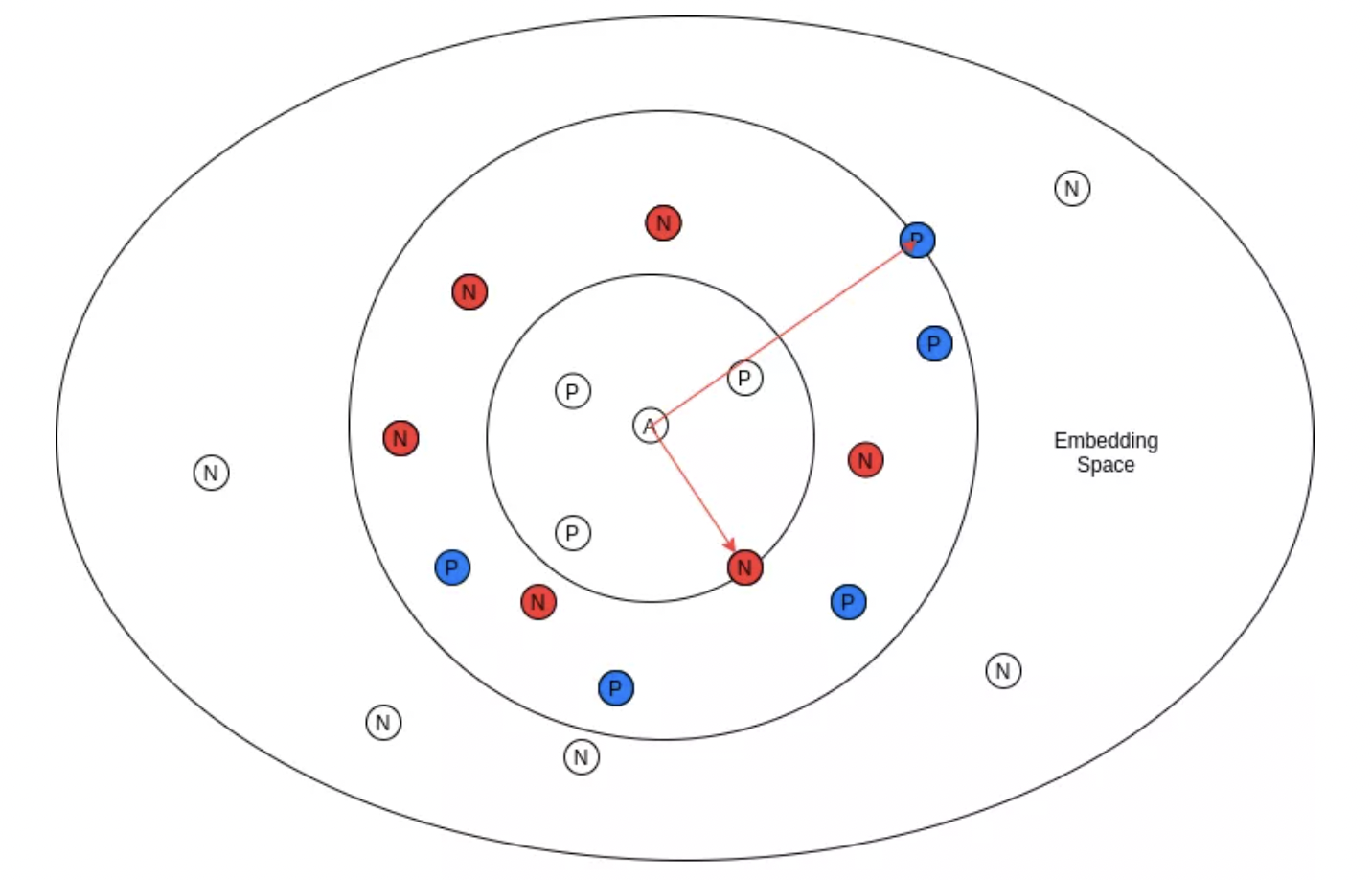
图:A = anchor, P = positives, N = negatives
3.1. 难负样本挖掘
公式如,
$$ S_{ij}^{-} > \text{min}_{y_k = y_i} S_{ik} - \epsilon $$
该式表明,只有那些与 anchor 样本的相似度大于正样本最小相似度的负样本才会包含在训练中. 对应于上图中所选择的是红色的负样本,因为它们都在与 anchor 的相似性最小的正样本的内部,其余的负样本都被丢弃.
3.2. 难正样本挖掘
$$ S_{ij}^{+} < \text{min}_{y_k \neq y_i} S_{ik} + \epsilon $$
该式表明,只有那些与anchor点相似度小于具有最大相似度(最接近anchor)的负样本的正样本才会被包括在训练中. 对应于上图中蓝色的困难正样本,其余的则被丢弃.
4. MS Loss 实现
research-ms-loss/multi_similarity_loss.py
import torch
from torch import nn
from ret_benchmark.losses.registry import LOSS
@LOSS.register('ms_loss')
class MultiSimilarityLoss(nn.Module):
def __init__(self, cfg):
super(MultiSimilarityLoss, self).__init__()
self.thresh = 0.5
self.margin = 0.1
#alpha
self.scale_pos = cfg.LOSSES.MULTI_SIMILARITY_LOSS.SCALE_POS
#beta
self.scale_neg = cfg.LOSSES.MULTI_SIMILARITY_LOSS.SCALE_NEG
def forward(self, feats, labels):
# feats: 图片的提取特征,l2 归一化的向量
# labels:图片的 GT 类别
assert feats.size(0) == labels.size(0), \
f"feats.size(0): {feats.size(0)} is not equal to labels.size(0): {labels.size(0)}"
batch_size = feats.size(0)
#相似性矩阵,l2归一化向量与其转置的点积
#sim_mat(i,j) - 行和列,对应于batch内第i个向量和第j个向量的相似性.
#sim_mat维度为 batch_size * batch_size.
#sim_mat的第0行对应于第0个向量与batch内其余向量的相似性.
sim_mat = torch.matmul(feats, torch.t(feats))
epsilon = 1e-5
loss = list()
for i in range(batch_size):
#第i个向量是 anchor.
#获取所有的正样本对,通过匹配与anchor具有相同类别标签的向量.
pos_pair_ = sim_mat[i][labels == labels[i]]
#移除样本对,通过计算anchor与其自身的相似性,如相似度为1的样本对.
pos_pair_ = pos_pair_[pos_pair_ < 1 - epsilon]
#获取所有的负样本对,通过匹配与anchor具有不同类别标签的向量.
neg_pair_ = sim_mat[i][labels != labels[i]]
#挖掘困难负样本,采用3.1所述方法.
#将值为0.1的margin加到负样本对相似性,以得到恰好位于边界的负样本.
neg_pair = neg_pair_[neg_pair_ + self.margin > min(pos_pair_)]
#挖掘困难正样本,采用3.2所述方法.
pos_pair = pos_pair_[pos_pair_ - self.margin < max(neg_pair_)]
if len(neg_pair) < 1 or len(pos_pair) < 1:
continue
#如果困难正样本和困难负样本都存在,则继续计算损失.
#加权
pos_loss = 1.0 / self.scale_pos * torch.log(
1 + torch.sum(torch.exp(-self.scale_pos * (pos_pair - self.thresh))))
neg_loss = 1.0 / self.scale_neg * torch.log(
1 + torch.sum(torch.exp(self.scale_neg * (neg_pair - self.thresh))))
#MS Loss公式
loss.append(pos_loss + neg_loss)
if len(loss) == 0:
return torch.zeros([], requires_grad=True)
#
loss = sum(loss) / batch_size
return loss基于 pytorch_metric_learning 的一种如下:
import torch
from pytorch_metric_learning import miners, losses
class MultiSimilarityLoss(torch.nn.Module):
def __init__(self, ):
super(MultiSimilarityLoss, self).__init__()
self.thresh = 0.5
self.epsilon = 0.1
self.scale_pos = 2
self.scale_neg = 50
self.miner = miners.MultiSimilarityMiner(epsilon=self.epsilon)
self.loss_func = losses.MultiSimilarityLoss(self.scale_pos, self.scale_neg, self.thresh)
def forward(self, embeddings, labels):
#难样本挖掘
hard_pairs = self.miner(embeddings, labels)
#损失计算
loss = self.loss_func(embeddings, labels, hard_pairs)
return loss5. 参考
[1] - Muti-Similarity Loss:考虑了batch中整体距离分布的对比损失函数 - 2020.09.25
[2] - Multi-Similarity Loss使用通用对加权进行深度度量学习-CVPR2019 - 2020.05.22 - 知乎