原文：Learning To Differentiate using Deep Metric Learning - 2020.10.04

作者：Jay Patel

基于 CNNs 的机器学习算法在有效视觉搜索领域取得了很大进展. 随着数据集的快速增长，目标识别模型能够识别物体，并在一定程度上泛化图像特征. 然而，当图像类别数据量巨大时，将其用于处理视觉搜索问题，面临如下问题：

[1] - 增长的物体类别数，同时会增加 CNN 网络倒数第二层的权重参数量. 由于其不断增长的模型大小，导致其很难在设备上部署.

[2] - 当图片类里仅有少量几张图片时，分类模型很难较好的收敛，使其很难在不同光照变化、尺度、背景复杂、缺失遮挡等情况时取得较好的效果.

[3] - 实际工程中，往往需要视觉搜索系统能够适用于多种产品生态系统，如数据集中没有满足的产品、随着地理位置或季节趋势发生变化等. 这些情况使其很难采用周期性或实时性的方式进行模型的训练或微调.

1. 深度度量学习

深度度量学习，DML，Deep Metric Learning，或 Distance Metric Learning.

DML 提出训练基于 CNN 的非线性特征提取模块(或编码器，encoder)，使得提取的具有语义相似性的图像特征(也叫嵌入，embeddings) 是相互临近的，而采用适当的距离度量(如 Euclidean 或 Cosine 距离)使得不相似的图像特征是彼此远离的.

再结合判别性分类算法，如 KNN，SVM、朴素贝叶斯等，对提取的图像特征进行目标识别，且不需要知道类别数. 这种训练的 CNN 模型所提取的特征的判别能力，既有紧凑的类内差异，又有可分离的类间差异. 这些特征还具有足够的泛化能力，即使是区分从未见过的类别.

图：给定两张图片-Chair和Table，度量学习的思想是，采用适当的距离度量方式评价两张图片的相似性. 当目的是区分目标，而不是识别目标时，由于不在依赖给定图像所属的类别，因此在很大程度上提高了模型的可伸缩性可扩展性.

下面采用基于 pair(对) 的 DML 训练流程，阐述CNN的训练和评估.

2. 问题阐述

假设 $X=\lbrace (x_i, y_i) \rbrace, i \in [1, 2, ...,n]$ 为包含 $n$ 张图像的数据集，其中 $(x_i, y_i)$ 表示第 $i$ 张图片以及对应的类别标签. 数据集总的类别数为 $C$，则 $y_i \in [1, 2, ..., C]$.

记 $f(x_i)$ 为图片 $x_i \in R^D$ 的对应特征向量(或特征嵌入)，其中 $f: R^D \rightarrow R^d$ 为参数为 $\theta$ 的深度网络模型. $D$ 和 $d$ 分别表示原始图像维度和特征维度.

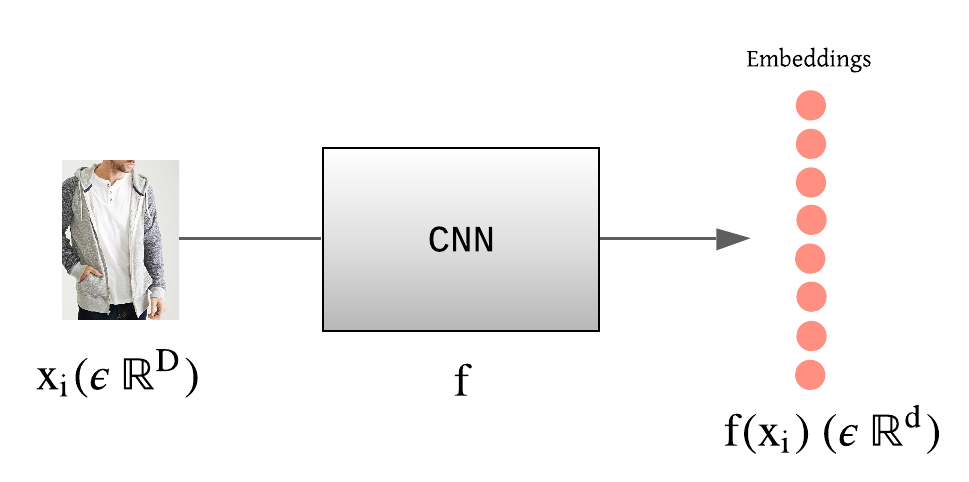
图：图片 $x_i$ 和由CNN提取的特征嵌入向量 $ f(x_i)$ 示例

一般定义两张图像特征之间的欧式距离为：

$$ D_{ij} = ||f(x_i) - f(x_j)||^2 $$

注，除了欧式距离之外，还可以是其它距离度量方式，如角度等.

为了学习距离度量函数 $f$，DML 算法一般采用相对相似性或绝对相似性约束，基于如图 Fig3 的 pair 对或 triplet 三元组的方法.

图像三元组可表示为 $(f(x_i), f(x_j), f(x_k))$，其中 $f(x_i)$、$f(x_j)$ 和 $f(x_k)$ 对应于 anchor $x_i$、正样本 $x_j$ 和负样本 $x_k$ 的特征向量. $x_i$ 和 $x_j$ 具有相同的类别标签，$x_i$ 和 $x_k$ 是不同的类别标签. 对应于图片对 $(x_i, x_j)$ 的特征向量对为 $(f(x_i), f(x_j))$. 具有相同类别标签的图像对表示正样本对，具有不同类别标签的图像对表示负样本对.

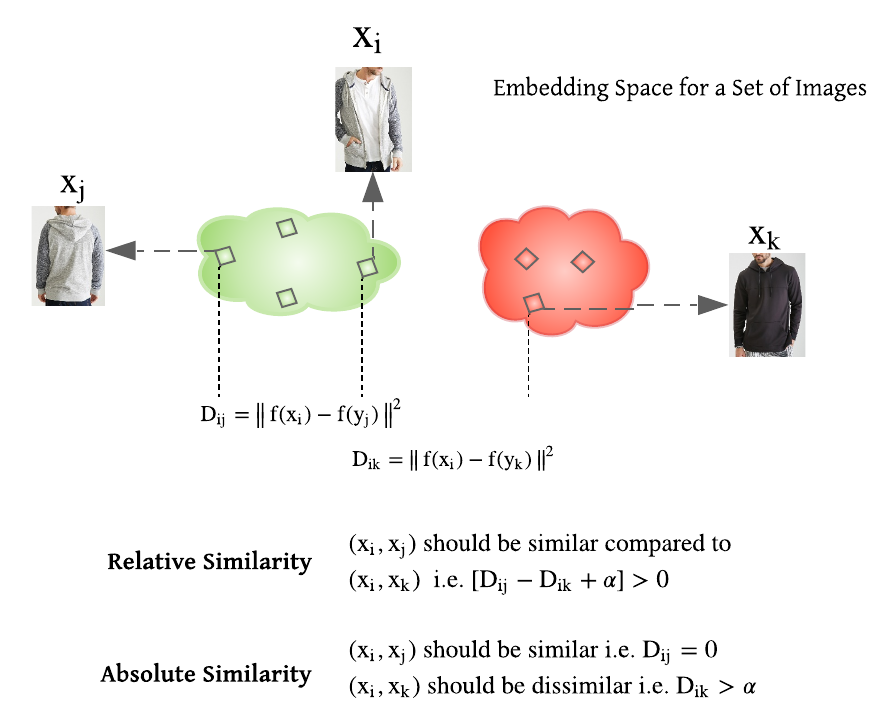
图Fig2：相对相似性约束和绝对性约束.

[1] - 相似性约束：

$R = \lbrace (x_i, x_j, x_k): x_i 和 x_j 比和 x_k 更相似 \rbrace $

$D_{ij} - D_{ik} + \alpha > 0$ 量化了 anchor-positive 图像对和 anchor-negative 图像对之间的相似性.

采用相对性约束的损失函数如，Triplet loss, N-pair loss, Lifted Structure, Proxy NCA loss.

[2] - 绝对性约束：

$S = \lbrace (x_i, x_j): x_i 和 x_j 相似 \rbrace$.

$D = \lbrace (x_i, x_k): x_i 和 x_k 不相似 \rbrace $.

$D_{ij}$ 和 $D_{ik}$ 分别量化了正样本图像对和负样本图像对的相似性.

采用绝对性约束的损失函数如，Contrastive loss, ranked list loss.

3. 模型训练

端到端的 DML 模型的训练流程如图.

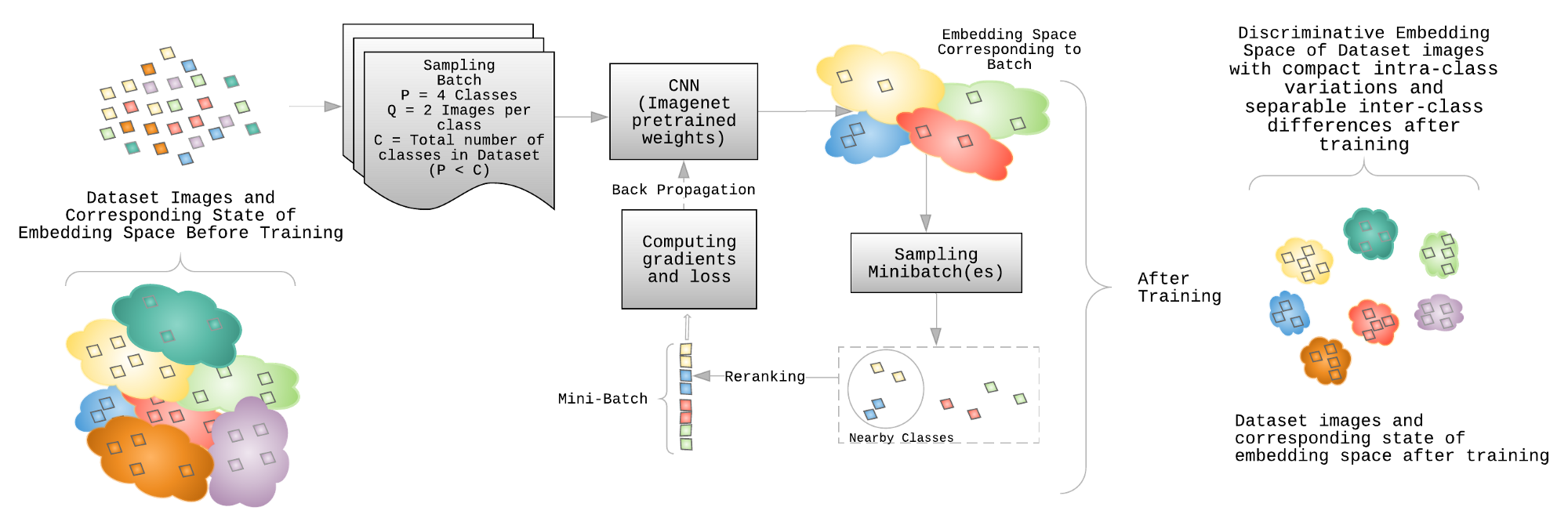
图：DML 训练流程.

最初，为了利用聚类不均匀(cluster inhomogeneity)的思想，对一批(batch)数据进行采样. 每个 batch 中包含 P 个类别、每个类别 Q 张图片. 采用这批数据，采用特定的采样策略，构建一个或多个 mini-batches.

3.1. 训练流程

[1] - Batch 采样：

Batchsize B，类别数目 P，每个类别的图片数量 Q.

[2] - 输入：

嵌入函数 $f$( ImageNet 数据集上预训练的 CNN 模型)，学习率lr b，batchsize B，类别数目 P，总的图片数为 B=PQ.

[3] - 特征提取：

给定参数状态 $\theta _t$，采用 CNN 对 batch 图像钱箱计算，得到图像特征嵌入 $f(x_i)$.

[4] - 采样：

从 batch 内进行 mini-batch 计算. 根据 batch 的大小，构建一个或多个 mini-batches 的特征向量.

[5] - 损失计算和训练

对于每个 minibatch 计算梯度和 BP，以更新参数状态 $\theta _t$ 到 $\theta_{t+1}$.

3.2. 损失函数

度量学习 - 损失函数汇总 - AIUAI

CNN 分类模型，一般是采用 Softmax Cross-Entropy (CE) Loss 损失函数.

而，DML 如果采用该损失函数，必须考虑的问题有：

[1] - Softmax Cross-Entropy (CE) Loss 可以看作是 max 操作子的 soft 版本. 如果采用常数隐私 $s$ 进行缩放，Logit 向量或类别概率并不影响给定图片的类目分配. 因此，可良好分离的特征具有更大的幅度，且能够促进类别的可分离性. 总之，这将导致特征分布呈放射状，如下图所示. 且，如果使用具有区分性的特征学习算法，如 KNN 分类器，对特征进行分类，则拥有不仅可分离而且可区分性的嵌入空间是至关重要的. 度量学习的损失函数旨在学习具有可区分性的特征空间.

图：给定数据集，训练的CNN模型倒数第二层提取的特征，投影到 2D 空间. 左：采用 Softmax loss 的2D特征分布；右：采用 DML 损失函数的可区分性特征分布.

[2] - CE Loss 并未直接利用 mini-batch 图像的结构性关系，因为每张图片(随机选取)是分别进行损失函数计算. 通过引入一种能够解决图像之间的语义差异性的惩罚，可以区分图像对或图像三元组的训练范式，以有效的检查图像之间的关系.

Lifted Structure Loss 充分利用 mini-batch 的数据，提升 mini-batch 的SGD 训练. 另一方面，三元组损失或对比损失分别利用图像三元组和图像对进行损失计算, Lifted Structure loss 提出采用成对距离度量 (O(m^2))，利用mini-batch 内所有的图像对(O(m)). 此外，相比于三元损失和对比损失，负样本仅是关于 一张 anchor 图像进行定义的，Lifted Structure Loss 同时利用给定图像对中的 anchor 样本和正样本，来从 mini-batch 内的图像中找寻其负样本.

Lifted Structure Loss 公式如：

$$ L_{i,j} = log(\sum_{(i, k) \in N} e^{(\alpha - D_{i,k})} + \sum_{(i, l) \in N}e^{(\alpha - D_{j, l})} ) + D_{i,j} $$

$$ L = \frac{1}{2|P|} \sum_{(i, j) \in P} max(0, L_{i,j})^2 $$

其中，$D_{i,j} = ||f(x_i) - f(x_j)||_2$ 为一个图像对之间的距离.

$D_{i,k}$ 和 $D_{j,l}$ 表示 mini-batch 内 anchor 和正样本与剩余负样本图像之间的距离.

$\alpha$ 表示距离间隔(margin).

$P$ 和 $N$ 分别表示 mini-batch 内所有的正样本对和负样本对.

3.3. 采样

直接对图像特征对进行处理，直观地会将目标引向学习有意思的图像嵌入. 因此，DML 一般都忽略标准的交叉熵损失函数.

DML 训练机制中，分别使用图像对或图像三元组的绝对相似性或相对相似性，在将图像输入到 CNN 时，需要有意义地采样图像 batches.

如果，数据集中用于前向计算的图像，mini-batch 大小，远大于数据集中总类别数，随机输入图像就能确保大多数图像样本能够在 mini-batch 具有相似类别标签的图像.

但是，如果数据集中包含大量的类别数，如，Standford Online Products 数据集，其图像类别数近 22000，mini-batch 随机采样可能得不到具有相同类别标签的图像对. 这种情况下，尽管每个 batch 都会遇到类间变化(因为存在不同类别标签的图像)，但无法解决类内变化(因为不一定有两张图像具有相同类别标签)，导致最终无法获得好的收敛效果.

尽管 DML 训练需要图像对或图像三元组的采样，但这种采样会分别使数据集的大小分别增加 O(m^2) 和 O(m^3). 此外，如果图像对或图像三元组是随机采样得到的，则随着训练的进行，大部分图像对或图像三元组贡献很小，因为并非所有的图像对或图像三元组会违反 margin $\alpha$(例如，三元组损失函数的情况). 很难计算有意义的损失，而且其不可避免的会减慢收敛速度.

为了克服这些问题，有很多不同的采样策略，以进行更快速和更好的训练收敛.

难负样本数据挖掘(Hard negative data mining) 策略是基于距离度量学习算法常用的手段. 其涉及难负样本和难正样本的计算，以构建给定 anchor 样本的正样本对和负样本对. 然而，当给定 batch 内包含大量的类别时，计算量是非常大的. 这种情况下，一般采用负样本类别挖掘，而不是负样本实例挖掘. 过程如下：

图：负样本类别挖掘采样

[1] - 对于给定参数状态 $\theta_t$，为了得到有意义的嵌入空间表示， 采样得到包含几百个类别的大的图像 batch(上面训练流程里是 P ). 对于每个图像对的损失函数，必须在给定 batch 中为每个给定类别分配 2 个图像样本. 例如，Stanford Online Products 数据集中，最少随机提取 2 张图片.

[2] - 对给给定 CNN 模型的给定参数状态 $\theta_t$，对 [1] 中采样的每张图片进行特征提取. 采用提取得到的图像特征得到类别表示向量或类别 proxies(嵌入向量).

[3] - 对于从 [1] 中采样的 P 个类别中每个随机选择的类别，采样其最临近的类别，并重排对应的图片. 这一步还可以采用基于 margin 的类别选择方法进行，如果一个类别违反距离 margin，则被选择作为给定 anchor 类别的最近邻类别.

[4] - 根据计算容量，构建一个或多个 mini-batch 的特征向量，以计算损失函数和梯度.

4. 模型评估和推断

相比于传统分类模型，图像被送入模型，得到类别概率，DML模型中，图像被送入提取图像特征. 这些图像特征被用于聚类和检索性能的评估.

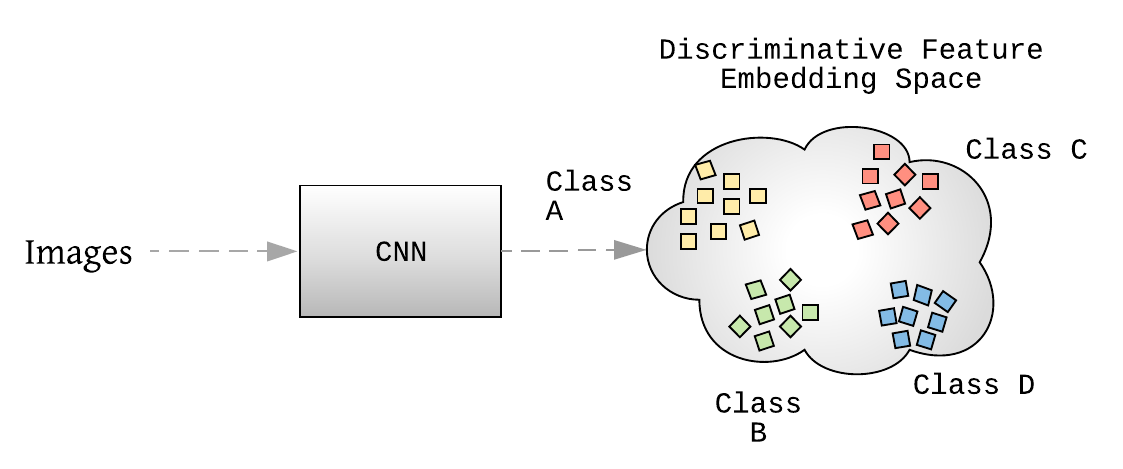
图：DML 推断流程. 图片被送入网络，以得到最后一层的特征向量. 由于是基于 DML 损失函数得到的，其具有可区分性的 2D 嵌入空间.

DML 特征评估的标准度量方式有：F1，NMI(Normalized Multual Information). 对于检索任务，recall@k 是常用的基准评测方式.

[1] - Recall@K

对于每个待查询图像(来自测试集)，采用适当的距离度量方式(如欧式距离，余弦距离)检索在相同测试集中的 K 个最近邻.

如果在检索到的 K 个最近邻结果中，存在一张图像和待查询图像属于相同的类别，则会返回 score 1.

Recall@K 表示对测试集中所有结果的召回数量.

[2] - F1

F1 的计算为：F1=2PR/(P+R)

[3] - NMI

对于输入的聚类集合 $\Omega$ 和 GT 聚类集合 $C$，NMI 为互信息(mutual information) 与聚类的平均熵和标签的熵的比值(NMI score is the ratio of mutual information and the average entropy of clusters and the entropy of labels).

$$ NMI = \frac{I(\Omega; C)}{2(H(\Omega) + H(C))} $$

其中，$\Omega = \lbrace \omega_1, \omega_2...\omega_n \rbrace$ 表示输入的聚类集合. $C = \lbrace c_1, c_2...c_n \rbrace$ 表示 GT 类别.

[4] - Acc@K

无监督分类模型的度量. 对于一张图片，采用适当的距离度量方式得到 K 个最近邻. 一张待查询图像根据 K 个最近邻结果中的最大数量以被分配到一个类别.

Acc@K 对测试集中每张待查询图像的结果求均值.

5. 总结

主要阐述了深度度量学习来解决目标识别问题. DML 模型具有如下优势：

[1] - 模型大小(model size) 不增加，因为模型训练的嵌入维度往往保持不变.

[2] - 由于目标是学习可区分性，而不是识别类别，因此可以对于每个类别仅有少量图片时，采用不同的采样策略进行训练和推断识别，即使是从未见过的类别.

[3] - 以周期性或在线方式微调到新的产品类别，都与梯度传播有关.

参考

1. Wang, X., Hua, Y., Kodirov, E., Hu, G., Garnier, R., & Robertson, N. M. (2019). Ranked list loss for deep metric learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 5207–5216).
2. Movshovitz-Attias, Y., Toshev, A., Leung, T. K., Ioffe, S., & Singh, S. (2017). No fuss distance metric learning using proxies. In Proceedings of the IEEE International Conference on Computer Vision (pp. 360–368).
3. Ranjan, R., Castillo, C. D., & Chellappa, R. (2017). L2-constrained softmax loss for discriminative face verification. arXiv preprint arXiv:1703.09507.
4. Wang, F., Xiang, X., Cheng, J., & Yuille, A. L. (2017, October). Normface: L2 hypersphere embedding for face verification. In Proceedings of the 25th ACM international conference on Multimedia (pp. 1041–1049).
5. Wu, C. Y., Manmatha, R., Smola, A. J., & Krahenbuhl, P. (2017). Sampling matters in deep embedding learning. In Proceedings of the IEEE International Conference on Computer Vision (pp. 2840–2848).
6. Wen, Y., Zhang, K., Li, Z., & Qiao, Y. (2016, October). A discriminative feature learning approach for deep face recognition. In European conference on computer vision (pp. 499–515). Springer, Cham.
7. Liu, Z., Luo, P., Qiu, S., Wang, X., & Tang, X. (2016). Deepfashion: Powering robust clothes recognition and retrieval with rich annotations. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1096–1104).
8. Oh Song, H., Xiang, Y., Jegelka, S., & Savarese, S. (2016). Deep metric learning via lifted structured feature embedding. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 4004–4012).
9. Sohn, K. (2016). Improved deep metric learning with multi-class n-pair loss objective. In Advances in neural information processing systems (pp. 1857–1865).
10. Schroff, F., Kalenichenko, D., & Philbin, J. (2015). Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 815–823).
11. Bellet, A., Habrard, A., & Sebban, M. (2013). A survey on metric learning for feature vectors and structured data. arXiv:1306.6709.
12. Hadsell, R., Chopra, S., & LeCun, Y. (2006, June). Dimensionality reduction by learning an invariant mapping. In 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06) (Vol. 2, pp. 1735–1742). IEEE. Chicago