论文:Deep Residual Learning for Image Recognition - CVPR2016
作者:Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun
团队:Microsoft Research
Github - Code-Caffe
Tutorial - ICML2016 tutorial
ResNet 网络已经用于很多应用场景,分类、目标检测、语义分割等等.
再次学习论文.
残差学习框架 ——使网络更深. ResNet 152层网络,是 VGGNet 的 8倍,却复杂度更低,在 ImageNet 上的错误率更低. 解决超深CNN 网络模型的训练(152层,1000层).
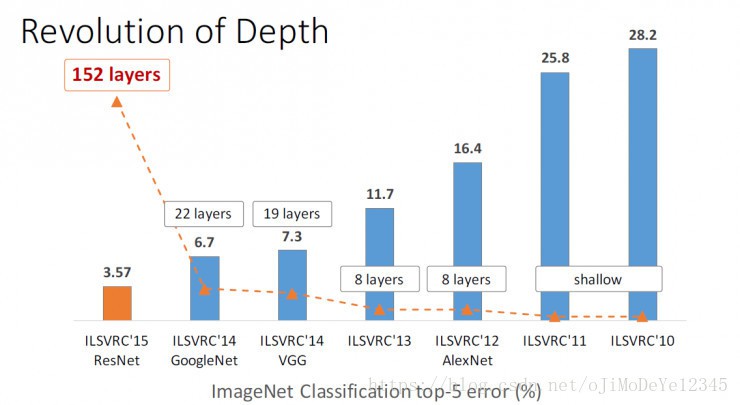
1. 介绍
网络比较深时,遇到的问题:
[1] - 网络深度的增加,遇到的一个问题是:学习更好的网络是否与堆积更多网络层一样简单(Is learning better networks as easy as stacking more layers?). 随着网络的加深,训练时会遇到梯度发散和消失(exploding/vanishing) 的问题. 其已有有效的解决方法是,初始化归一化(normalized initialization) 和 网络中间归一化网络层(intermediate normalization layers,BN 层). 确保几十层的网络 可以SGD 训练到收敛.
[2] - 网络深度加深,并训练收敛后,会遇到精度衰退(degradation) 的问题: 随着网络的加深,精度开始饱和(saturated),然后快速的衰退. 而衰退的原因并不是过拟合造成的. 更深的网络深度得到训练误差也较高. 如 Figure 1.
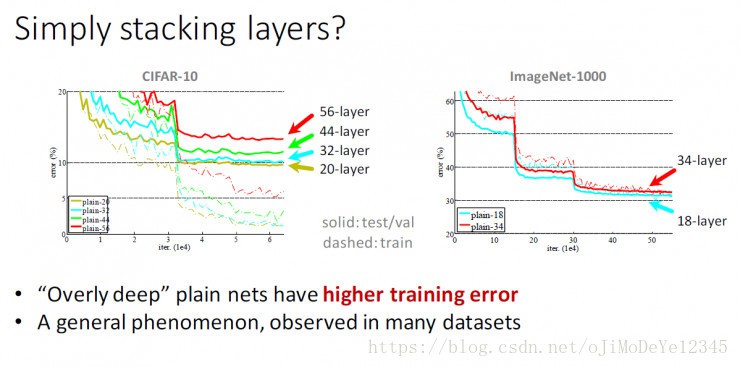
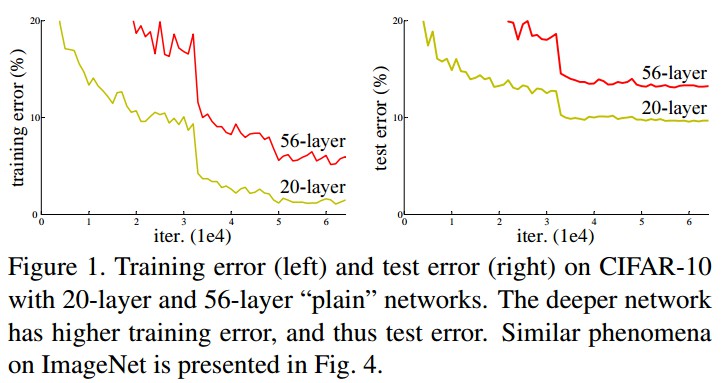
训练精度的衰退说明了不是所有的系统都是一样容易优化的.
ResNet 提出利用深度残差学习框架来处理由于网络加深而造成的精度衰退(degradation)问题. 如 Figure 2.
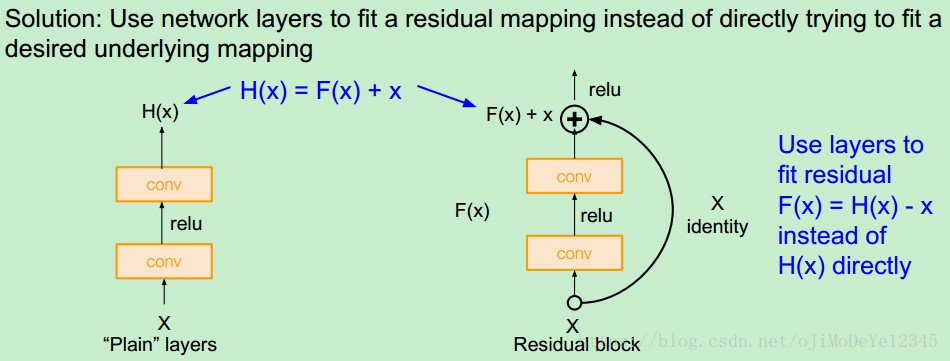
记希望的网络层映射为 $H(x)$,采用堆积非线性层(stacked nonlinear layers) 来拟合另一个映射 $ F(x) := H(x)-x$. 则,原来的网络映射即是 $F(x)+x$.
假设残差映射 $F(x) + x$ 的优化比原映射 $H(x)$ 的优化更容易.
极端情况,如果某恒等映射 $x$ 是最优的,则将残差设为 0 比采用堆积非线性层来拟合横等映射更容易.
残差映射 $F(x) + x$ 可以采用 shortcut 连接(shortcut connections) 的前馈神经网络实现. 如 Figure 2. shortcut 连接用于跳过一个或多个网络层. ResNet 利用的 shortcut 连接被简化为执行恒等映射,并将恒等映射的输出与堆积网络层的输出相加. 如 Figure 2.
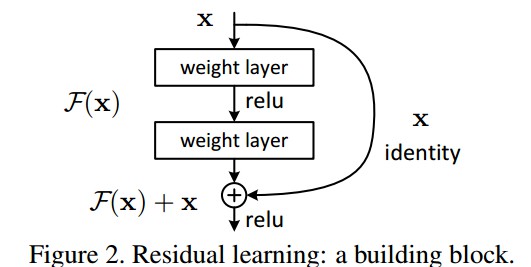

恒等映射不会增加参数量和计算复杂度.
基于此构建的深度网络结构仍可以采用 SGD 进行 End-to-end 的网络训练. 采用 Caffe 等深度框架很容易实现,且不需要更改对应的 solvers 参数.
2. Deep Residual Learning
2.1. 残差学习
记 $H(x)$ 为采用多个堆叠网络层拟合的映射(不必是整个网络,可以是网络的一部分层),$x$ 为堆叠网络层的第一层的输入.
假设,多个非线性层能够逼近任何复杂函数,那么可以假设,这些网络层可以拟合残差函数,如 $H(x)-x$. (假设输入和输出维度相同.)
故,采用多个非线性网络层来逼近残差函数 $F(x) := H(x)- x$. 则,原来的映射 $H(x)$ 变为 $ F(x) + x$.
这种表示是受衰退(degradation)问题的反常现象的启发(如 Figure1 左). 正如前面讨论过的,如果新增的网络层能够构建为恒等映射形式,那么,更深层的网络模型应该比其对应浅层网络模型的训练错误率更小. 衰退问题说明了 solvers 采用多个非线性层难以逼近恒等映射.
基于变形后的表示,如果恒等映射是最优的,则 solvers 可以将多个非线性层的网络权重趋向于 0 来逼近恒等映射.
虽然实际情况中,恒等映射不可能是最优的,但这种表示形式对于衰退问题的预处理是有益的. 如果最优函数逼近于恒等映射,而不是逼近于 0 映射,则相比较于学习新的函数,solver 能够更容易找到关于恒等映射的扰动.
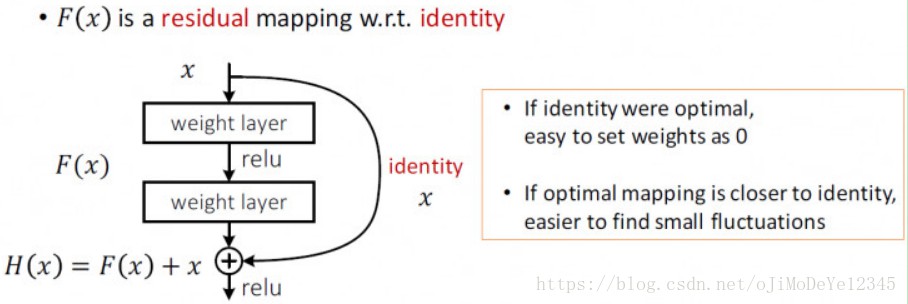
2.2 基于 Shortcuts 的恒等映射
对每几个堆积网络层进行残差学习,一个残差学习构建模块如 Figure 2. 其定义:
$$ f(y) = F(x, \lbrace W_i \rbrace) + x $$
其中,$x$ 和 $y$ 是残差模块的输入和输出向量.
函数 $F(x, W_i)$ 是待学习的残差映射.
如 Figure 2 中,两个网络层,$F=W_2 \sigma(W_1 x)$. $\sigma$ 表示 ReLU,这里忽略了 biases 项,简化表示. 操作 $F +x$ 是通过 shortcut 连接和 element-wise addition 来实现. 在 addition 后,再执行一次非线性操作(如 $\sigma(y)$).
残差模块的公式可知,shortcut 连接既不会增加额外的参数,也不会增加计算复杂度. $x$ 和 $F$ 的维度必须一致. 如果不一致时(如,改变输入或输出通道channel),可以通过 shortcut 连接执行线性投影 $W_s$(方阵),以匹配维度:
$$ y = F(x, \lbrace W_i \rbrace) + W_s x $$
残差函数 $F $ 的形式是灵活的. 可以是包含两层或三层的函数(如 Figure 5),也可以是更多的层. 但如果 $F$ 仅只有一层,则残差模块类似于线性层: $y = W_1 x + x$,不具有优势.
此外,虽然是以全连接层为例,但也适用于卷积层. 函数 $F(x, \lbrace W_i \rbrace $ 可以表示为多个卷积层. 然后对两个 feature maps 进行逐通道(channel by channel)的 element-wise addition.
2.3. 网络结构
通过对许多 plain/residual 网络分析,这里以 ImageNet 的两个模型为例. 如 Figure 3.
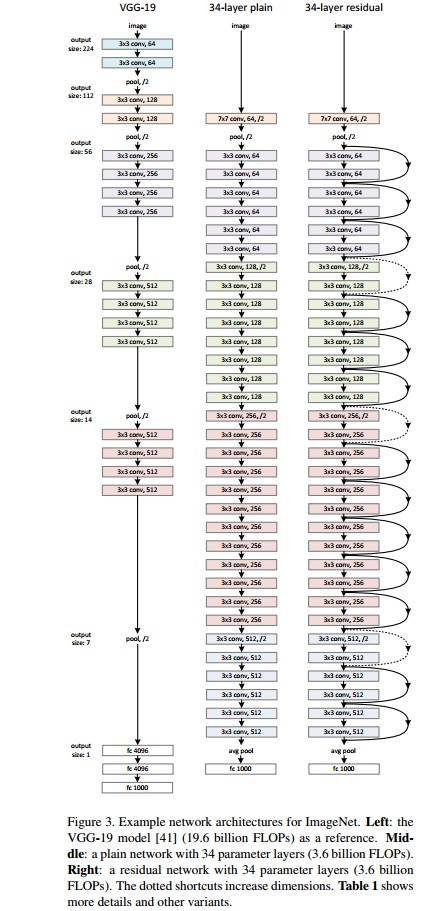
网络结构:
Plain Network: plain baselines 基于 VGGNets的启发(如,Figure 3 左.) 卷积层大部分是 3 ×3 fliters. 其设计遵循两个原则:
[1] - 对于相同输出的特征图尺寸,网络层 filters 数量相同;
[2] - 如果特征图的尺寸减半,网络层 filters 数量加倍,以保持每一网络层的时间复杂度一致.
采用步长为 2 的卷积来直接进行下采样. 并在网络的最后采用全局平均池化层(global average pooling) 和一个 1000-way 的全连接层和 softmax . 如Figure3 中间的网络结构,共有 34 个权重网络层. 相比较于 Figure3 左边的 VGGNet 网络,34 层网络结构具有 更少的filters 和 更低的复杂度. Residual Network: shortcut 连接的的残差网络如 Figure 3 右边图. 在输入和输出维度一致时,可以直接使用恒等映射 shortcuts(图中实线). 当维度增加时(图中虚线),考虑两种情况:
[1] - shortcut 仍执行恒等映射,对增加的维度部分采用补零处理;不引入新的参数.
[2] - 采用公式 2 中的投影 shortcut,匹配维度保持一致(利用 1×1 卷积).
以上两种方案,当 shortcuts 跨越两种尺寸的特征图时,卷积步长stride 均为 2.
2.4 实现
[1] - 基于 ImageNet.
[2] - 图片 resized 短边范围到 [256, 480],数据尺度scale 增广.
[3] - 随机裁剪 224×224,水平翻转,减均值.
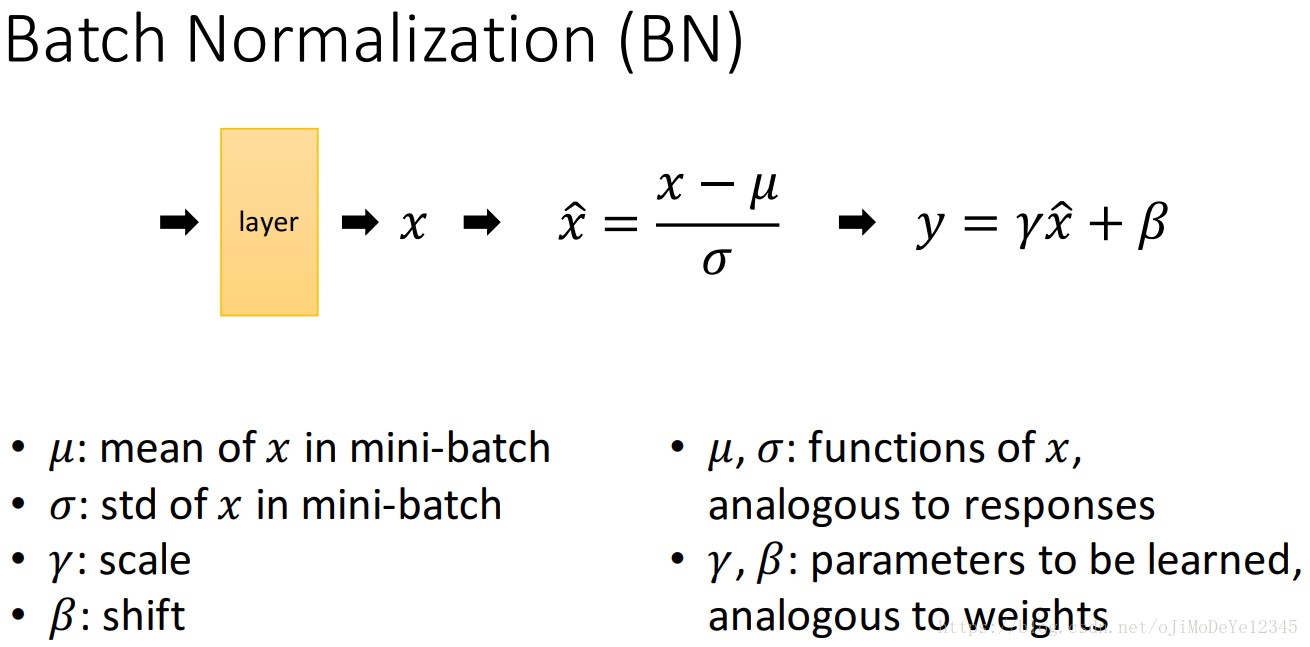
[4] - 每个卷积层和激活层之间加入 BN 层.
[5] - 网络权重初始化,手动训练 plain 网络和残差residual 网络.
[6] - SGD,batchsize=256.
[7] - 初始学习率为 0.1,当error停滞时,降低学习率 ×0.1,模型训练 $60×10^4$ 次迭代.
[8] - weight decay 为0.0001,momentum为 0.9.
[9] - 未使用 dropout层.

3. Experiments
3.1 ImageNet 分类结果
1000 类. 实验结果:
Plain Networs:
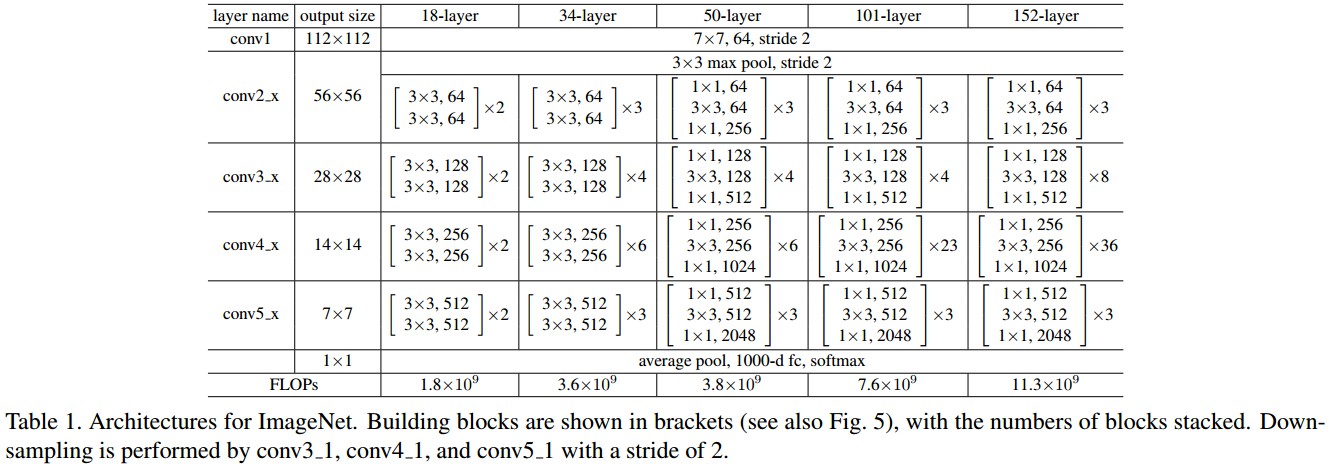
首先对 18-层和34-层 plain 网络(Figure 3 图中)分析. 网络结构如 Table 1.
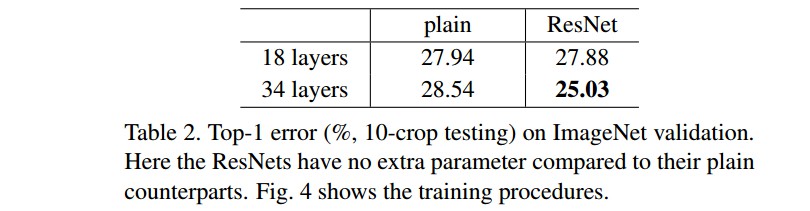
34层网络具有更高的 validation error.
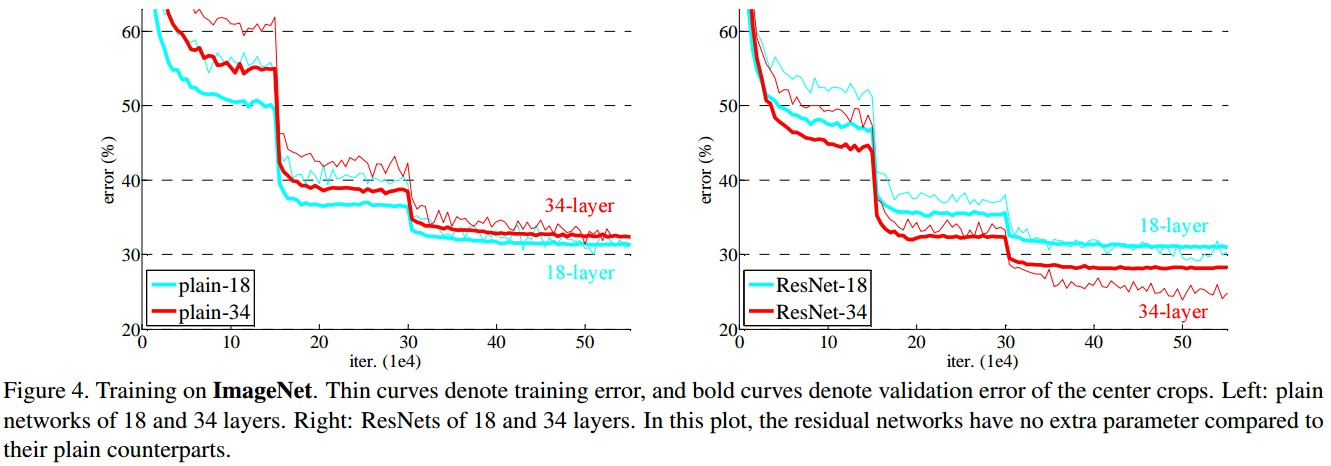
Figure 4 给出了训练过程中 training/validation error. 可以看出衰退degradation 问题,34-层 platin 网络在整个训练过程都具有较高的 training error,并分析其不是由梯度消失引起的.
Residual Networks:
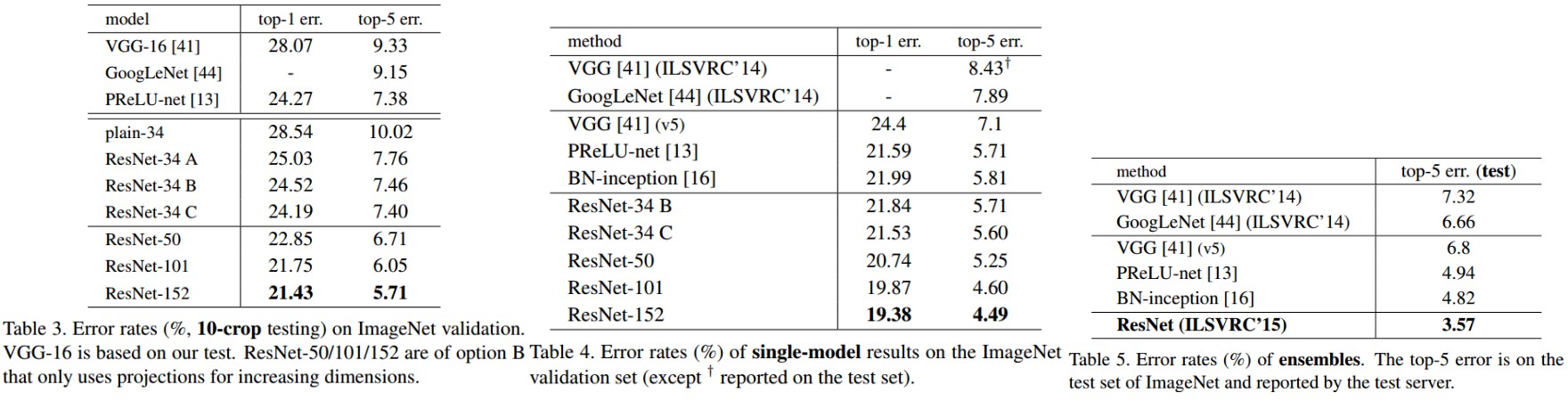
18-层和 34 -层残差网络(ResNets). baseline 网络结构与 plain 网络结构相同,除了在每对 $3×3$ filters 后添加一个 shortcut 连接,如 Figure 3 右图. 34 层的 ResNet 比 18 层的效果更好. 且 34 层 ResNet 具有更低的训练误差,即:衰退degradation 问题得到了很好的解决.
恒等映射与投影shortcuts:
恒等映射被证明是有助于网络训练的.
3.2 CIFAR-10 分类结果
CIFAR-10 数据集,50k training 图片,10k testing 图片,10 类.
[1] - 网络输入是 32×32 的图片,减均值处理;
[2] - 网络第一层是 3×3 Conv.
[3] - $6n$ 层 3×3 Conv 的堆积层,分别的到 feature maps 尺寸 $32, 16, 8$.
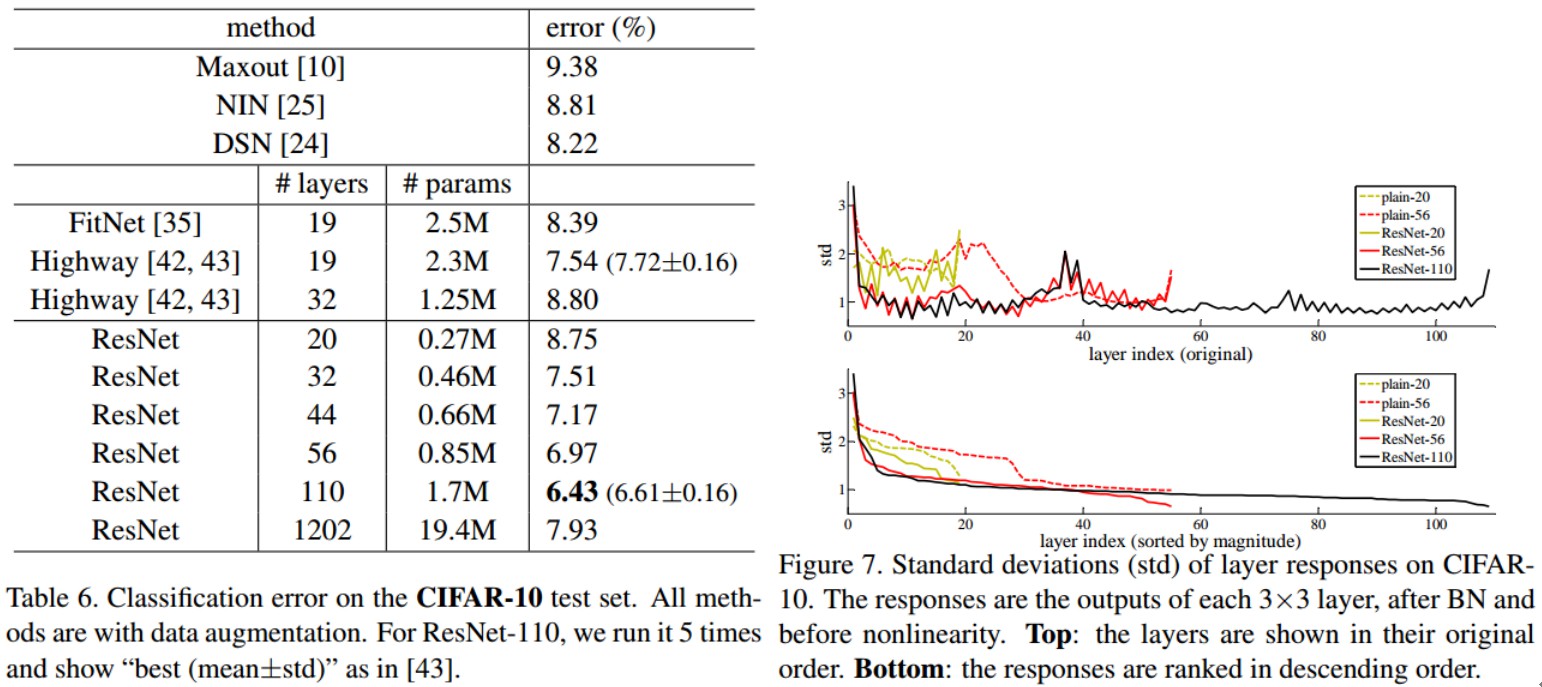
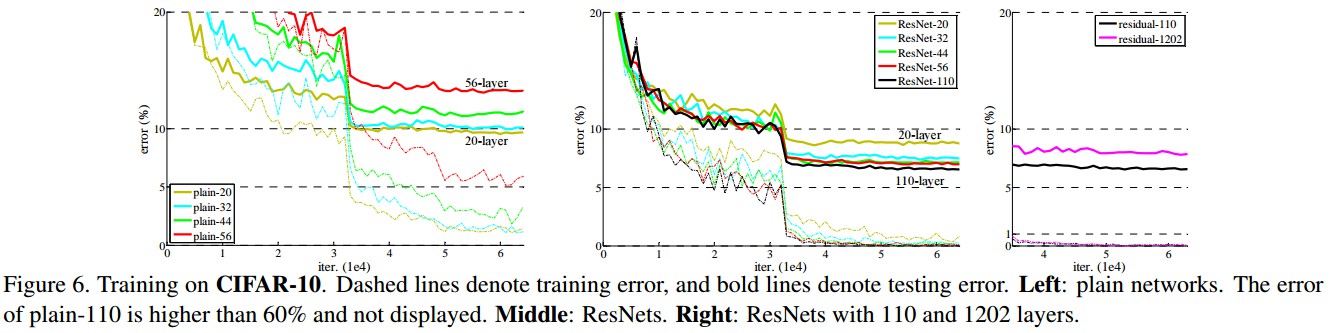
3.3 PASCAL 和 COCO 目标检测结果
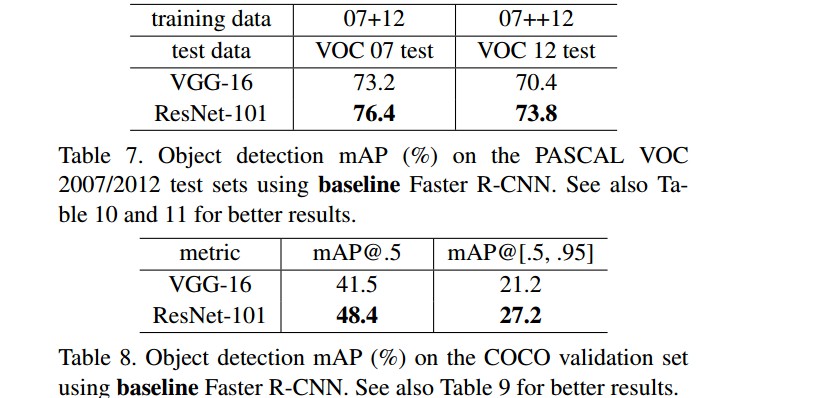
Related
[1] - 秒懂!何凯明的深度残差网络PPT是这样的|ICML2016 tutorial
[2] - 对ResNet的理解
[3] - [Feature Extractor[ResNet]](http://www.cnblogs.com/shouhuxianjian/p/7766441.html)