题目: Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
作者: Sergey Ioffe, Christian Szegedy
团队: Google
在 PSPNet 与 DeeplabV3中,有对 BN 层对语分割有效性的使用,故再次对 BN 层提出的论文阅读学习,并理解其 Caffe 实现.
DeeplabV3 中关于 Batch Normalization 的使用如下:
在 ResNet 所添加的模块中包括对 BN 参数的学习,作者发现,BN 层对于网络的训练也很重要.
鉴于 BN 参数的训练需要较大的 batch size,DeeplabV3 采用 _output_stride=16_,_batch_size =16_, BN 的 _decay=0.997_,_initial_learning_rate=0.007_.
在训练集上训练 30K 次迭代后,固定 BN 参数,并采用 output_stride=8 在 PASCAL VOC 2012 训练集上,采用小的 _base learning rate=0.001_, 再训练 30K 次迭代.
神经网络训练面对的问题:
- 每一网络层的输入的分布在训练过程中都随着前一层参数的变化而发生变化;
- 需要较低的学习率和慎重的参数初始化,影响训练速度;
- 难以利用饱和非线性的进行模型训练.
即 intenal covariate shift(内部相关变量偏移).
BN 层的作用:
- 允许使用较高的学习率和不太严格的初始化.
- 也可以作为正则项;
- 在某些场合下可以减少对 Dropout 的需要.
- Batch Normalization 针对当前的图像分类模型,在取得相同精度的情况下,训练时间减少了 14 倍.
1. Introduction
SGD 优化的目标损失函数:
${ \Theta = arg min_{\Theta} \frac{1}{N} \sum_{i=1}^N l(x_i, \Theta) }$
其中,
${ \Theta }$ - 网络参数
${ x_{1...N} }$ - 训练数据集
基于SGD优化方法,对网络进行逐步训练,每一步只需处理 mini-batch 的训练数据 ${ x_{1...m} }$. 采用 mini-batch 的训练数据来逼近 loss 函数关于参数的梯度:${ \frac{1}{m} \frac{\partial l(x_i, \Theta)}{\partial \Theta} }$.
采用 mini-batch 的方式,与每次单个样本进行训练相比,
- mini-batch 训练的 loss 所计算的梯度更能反应整体训练集,尤其 batch size 较大时;
- mini-batch 的计算,相对于单独计算 m 次的叠加,对于现在的并行化计算更有效率.
虽然 SGD 简单有效,但是对于模型的超参数仍需仔细设置,尤其是优化的 learning rate 与模型参数的初始值. 由于每层的输入都受到先前网络层参数的影响,哪怕网络参数发生细微的变化,都会导致结果不理想,尤其深层网络.
网络层需要不断的对不同的输入数据进行处理,会出现 covariate shift 问题.
假设对于网络计算:${ l = F_2(F_1(u, \Theta _1), \Theta _2) }$,${F_1}$ 和 ${F_2}$ 是任意的变换函数,${\Theta _1}$ 和 ${\Theta _2}$ 是最小化 loss ${l}$ 所需学习的参数.
参数 ${ \Theta _2 }$ 的学习,可以看作是,对输入为 ${ x=F_1(u, \Theta _1) }$ 的子网络 ${ l = F_2(x, \Theta _2) }$ 的优化.
基于 梯度下降法,${ batchsize = m }$,${ learning \ rate = \alpha }$,
${ \Theta_2 \leftarrow \Theta_2- \frac{\alpha}{m} \sum_{i=1}^m \frac{\partial F_2(x_i, \Theta_2)}{\partial \Theta _2} }$
一个标准的 输入为 x 的网络 ${ F_2 }$ 的优化问题.
因此,如果输入 x 的分布能够一直保持固定,对于网络的训练是有帮助的. ${\Theta _2}$ 就不需要再对 x 的分布变化进行调整.
子网络输入数据分布固定对于处理子网络外的其他层也是有利的.
以 Sigmoid 激活函数为例,
Sigmoid 激活函数层 ${ z = g(Wu + b) }$,u 是网络层输入,权重矩阵 W 和偏置向量 b 是待学习参数,${ g(x) = \frac{1}{1 + exp(-x)} }$. 将数值变换到 [0, 1],很大的负数变为0,很大的正数变为 1.
随着 |x| 的增加,${ g(x) }$ 的梯度(导数) ${g^{\prime}(x)}$趋近于 0.
${ g^{\prime}(x) = (\frac{1}{1 + exp(-x)})^{\prime} = \frac{exp(-x)}{(1 + exp(-x))^2} = \frac{1 + exp(-x)- 1}{(1 + exp(-x))^2} }$
${ g^{\prime}(x) = \frac{1}{(1 + exp(-x))}(1- \frac{1}{(1 + exp(-x))}) = g(x)(1- g(x)) }$
Sigmoid 函数饱和,会导致梯度消失. 当函数值接近 0 或 1 时,即饱和;局部梯度接近 0, 导致梯度消失.
常用的解决方法是采用 ReLU(x) = max(x, 0) 和良好的初始化.
如果能够保证网络的非线性输入的分布能够在网络训练过程中一直保持稳定,就可以减少饱和的可能,加速网络训练.
对于深度网络训练过程中所出现内部节点的分布变化,这里称之为 Internal Covariate Shift(ICS).
Internal Covariate Shift 是由于训练过程中网络参数的变化而导致网络激活值的分布发生的变化.
提出采用 Batch Normalization 来对 ICS 进行消除,加速网络训练. 其主要是采用 normalization 处理来固定网络层输入的均值和方差(means and variances).
- 减少了网络的梯度计算对于参数 scale 和初始值的依赖.
- 允许使用更大的 learning rates,而不出现发散.
- 具有对模型的正则作用;
- 能减少对 Dropout 的使用;
- 能避免网络进入饱和状态进而利用网络的饱和非线性.
2. 减少 Internal Covariate Shift 所进行的探索
白化(whiten),将数据变换到均值为 0,方差为1,并去数据相关性. 通过将每一层的输入进行白化处理,可以固定数据的分布,移除 internal covariate shift 的负影响.
训练过程中每一步的白化处理,可以通过直接修改网络,或者修改作用于网络激活值的优化参数. 但是,如果在优化过程中混杂着这些修改,可能会导致梯度下降时需要对参数进行更新.
例如,假设网络层输入是 u ,需要学习的 bias b,x = u+b,则归一化即是对训练数据减去均值:${ \hat{x} = x- E[x] }$. 训练数据集 ${ \chi = {x_{1...n}} }$ ,${ E[x] = \frac{1}{N}\sum_{i=1}^N x_i }$.
如果梯度下降忽略 E[x] 对 b 的影响,则 b 的更新公式是:
${ b \leftarrow b + \Delta b }$,其中 ${ \Delta b \propto- \frac{\partial l}{\partial \hat{x}} }$.
${ u + (b + \Delta b)- E[u + (b + \Delta b)] = u + b- E[u +b] }$.
因此,更新参数 b 以及后面归一化处理,均不会影响网络层的输出,以及 loss值. b 值会随着训练的进行而不断的增加,但 loss 保持不变. 如果不只是中心化处理,还进行尺度(scales the activations)处理,这种情况会更严重.
实验发现,当在梯度计算之外,计算归一化,则会导致模型爆炸(不收敛).
上述描述的问题是由于梯度下降优化算法没有考虑归一化. 我们想要的是,对于任何参数值,网络总能根据想要的分布来产生激活值. 这就需要 loss 的关于模型参数的梯度要将归一化以及归一化对于模型参数 $\Theta$ 的依赖性考虑在内.
假设网络层输入为向量 x,${ \chi }$ 是训练数据集,归一化处理记为:${ \hat{x} = Norm(x, \chi) }$,其不仅与给定训练的训练样本 x 相关,还与所有的训练样本 ${ \chi }$ 相关(如果 x 是由其它网络层得到,则 ${ \chi }$ 的每一个都与 ${ \Theta }$ 相关.). 对应的反向传播计算为,${ \frac{\partial Norm(x, \chi)}{\partial x} }$,${ \frac{\partial Norm(x, \chi)}{\partial \chi} }$ . 如果忽略后一项,则会导致网络爆炸.
在这里,对网络层输入的白化处理计算量大,需要计算协方差矩阵 ${ Cov[x] = E_{x \in \chi}[xx^T]- E[x]E[x]^T }$ 以及其平方根倒数(inverse square root),以得到白化结果 ${ Cov[x]^{-\frac{1}{2}}(x- E[x]) }$. 还需要计算对应的反向传播的偏微分.
这显然是需要寻找一种能够进行输入归一化,可微分的,且不需要每次参数更新都对整个训练数据进行重新分析的处理方法.
3. 基于Mini-Batch 统计的归一化
由于对每一层输入的白化处理计算量大,且不是完全可微的,这里进行了两处必要的简化:
[1] - 对每一个标量特征进行独立归一化,使其均值为 0 ,方差为1,而不是对网络层输入和输出的全部特征进行白化;
假设网络层的输入是 d 维输入 ${ x=(x^{(1)}...x^{(d)}) }$,对每一维进行归一化,${ \hat{x} ^{(k)} = \frac{x^{(k)}- E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}} }$ . 这里的期望和方差是在训练数据集上计算的.
但是这种对网络层的每一维输入进行归一化,可能改变网络层所表示的内容. 例如,对 Sigmoid 的输入进行归一化,可以将输入约束到非线性的线性区域,这就是 Sigmoid 层能表达的非线性特点改变了. 因此,需要保证插入到网络的变换能表示相同的变换. 对于每一个激活值 ${ x^{(k)} }$,引入一对参数 ${ \gamma ^{(k)} }$ 和 ${ \beta ^{(k)} }$ 来分别作为缩放和平移归一化值,即:
${ y^{(k)} = \gamma ^{(k)} \hat{x} ^{(k)}+ \beta ^{(k)} }$
参数 ${ \gamma ^{(k)} }$ 和 ${ \beta ^{(k)} }$ 是可以和网络模型参数一起学习,并能重构网络的表征能力. 即,通过设置 ${ \gamma ^{(k)} = \sqrt{Var[x^{(k)}]} }$,${ \beta ^{(k)} = E[x^{(k)}] }$ 就可以重构原始的激活值.
[2] - 由于对 mini-batches 采用随机梯度算法进行训练,故,这里对每一个 mini-batch 计算每个激活值的均值和方差.
假设 m 个样本的 mini-batch ${ \mathcal{B} }$ ,因为是对每一个激活值分别独立进行归一化,这里以其中的一个 ${ x^{(k)} }$ 为例(为了方便,忽略 k,简写为 x).
${ \mathcal{B} = [x_{1...m} ] }$
记归一化值为 ${ \hat{x}_{1...m} }$,对应的线性变换为 ${ y_{1...m} }$,则 Batch Normalization Transform 可记为:
${ BN_{\gamma, \beta}:x_{1...m} \rightarrow y_{1...m} }$
算法1 - BN具体算法如下: </p>
</p>
${ \gamma }$ 和 ${ \beta }$ 是待学习参数,但 BN 变换不是单独处理每个训练样本的激活值,${ BN_{\gamma, \beta}(x) }$ 需要对 mini-batch 内的训练样本和其它样本处理. 缩放和平移后的 ${y}$ 值传递到其它网络层. 归一化的激活值 ${ \hat{x} }$ 只存在于 BN 变换层内,但也是很重要的. 只要每个 mini-batch 内的各元素都是相同分布采样的,且忽略 ${ \epsilon }$ ,则 ${ \hat{x} }$ 的分布的期望值是 0,方差是 1,${ \sum_{i=1}^{m}\hat{x}_i = 0 }$,${ \frac{1}{m} \sum_{i=1}^{m}\hat{x}_i^2 = 1} $.
训练时的梯度计算,根据链式法则,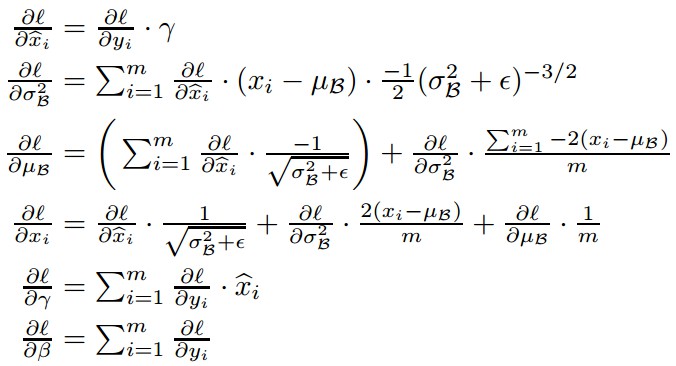
BN 层是可微分的,能够保证模型的训练,且训练时网络层的分布具有较小的 internal covariate shift,加速模型训练.
3.1 基于 Batch-Normalized 的网络训练和部署
未添加 BN 层,网络层的输入是 x;添加 BN 层后,网络层的输入是 BN(x),即可采用SGD等进行网络训练.
BN 层有助于网络训练,但在 inference 阶段则是不必要的,网络输出只与输入相关. 因此,网络训练完成后,归一化操作为:
${ \hat{x} = \frac{x- E[x]}{\sqrt{Var[x] + \epsilon}} }$
其中,${ Var[x] = \frac{m}{m-1} \cdot E_{\mathcal{B}}[\sigma_{\mathcal{B}}^2] }$,无偏估计方差,在 m 个样本的训练 mini-batch 计算期望值,${ \sigma_{\mathcal{B}}^2 }$ 是样本方差.
Inference 阶段均值和方差是固定的,归一化是对每个激活值的简单线性变换.
Batch-Normalized 网络的训练过程如下:
算法2 - BN网络的训练
3.2 Batch-Normalized 卷积网络
BN层可以应用于网络的任何地方,这里以逐元素非线性仿射变换为例:
${ z = g(W\mathbf{u} + b) }$
其中, W 和 b 是模型待学习参数,${ g(\cdot) }$ 是非线性函数,如 Sigmoid 和 ReLU. 全连接层和卷积层也可以记为这种表达式形式.
在线性变换前加入 BN 变换,即归一化 ${ x = W\mathbf{u} + b }$.
这里也可以对网络层输入 ${ \mathbf{u} }$ 进行归一化,但是由于 ${ \mathbf{u} }$ 可能是其它非线性的输出,其分布的会随着训练而发生变化,对其进行处理不能很好的消除 covariate shift. 相对而言,${ W\mathbf{u} + b }$ 就更可能是对称、非稀疏的分布,“more Gaussian”. 这种归一化更能使激活值保持稳定的分布.
这里,由于是对 ${ W\mathbf{u} +b }$ 归一化,偏置项 b 的影响经减均值处理可以忽略. 因此,${ z = g(W\mathbf{u} + b) }$ 可以转化为:
${ z = g(BN(W\mathbf{u})) }$
BN 独立地对 ${ x=W\mathbf{u} }$ 的每一维进行处理,每一维学习参数对 ${ \gamma^{(k)}, \beta^{(k)} }$.
对于卷积层,其卷积属性也是需要的,相同 feature map 的不同位置的不同元素,采用相同的方式进行处理. 为此,可以对 mini-batch 内的全部激活值联合归一化. 在算法1中,假设 ${ \mathcal{B} }$ 是跨越 mini-batch 内所有元素和空间位置的特征图的全部值集合,即,当 mini-batch = m,feature map 尺寸为 p×q 时,mini-batch 的有效值应为 ${ m^{\prime} =|\mathcal{B}|=m \cdot pq }$.
对每个 feature map 学习参数对 ${ \gamma^{(k)}, \beta^{(k)} }$,而不是对每一个激活值学习参数.
3.3 BN 可以有 higher learning rates
传统的深度网络训练中,太大的学习率会导致梯度发散或消失,或者较差的局部最小值.
BN 层能够帮助解决这种问题.
通过归一化网络的激活值,能够阻止参数的细微变化被放大,或者激活值的梯度次优变化. 例如,BN 能够避免网络训练陷入饱和非线性状态.
BN 还能够使网络更好的适应参数尺度. 正常情况下,学习率较大会增加网络层参数的尺度,接着会增大BP时梯度,导致模型发散.
但,加入 BN 层后,网络层的 BN是不受参数尺度影响的.
对于标量 ${ a }$,
${ BN(W\mathbf{u}) = BN((aW)\mathbf{u}) }$
${ \frac{\partial{BN((aW)\mathbf{u})} }{\partial \mathbf{u}} = \frac{\partial{BN(W\mathbf{u})} }{\partial \mathbf{u}} }$
${ \frac{\partial{BN((aW)\mathbf{u})} }{\partial W} = \frac{1}{a} \cdot \frac{\partial{BN(W\mathbf{u})} }{\partial W} }$
可以看出,尺度不会影响梯度的BP. 而且,较大的权重会使梯度值变小.
因此,BN 可以确保参数增长的稳定性.
此外,BN 还可以使网络层的 Jacobians 的奇异值接近 0,更有利于训练.
3.4 BN 对模型的正则
网络加入 BN 后进行训练时,一个训练样本是与 mini-batch 内的其它样本共同处理的,网络不是只有给定的训练样本来得到决策值. 这对于网络的泛化是有利的.
Dropout 是一种常用的降低网络过拟合的方法;但,在加入 BN 的网络中,Dropout 是可以被去除或者大量减少的.
4. Experiments
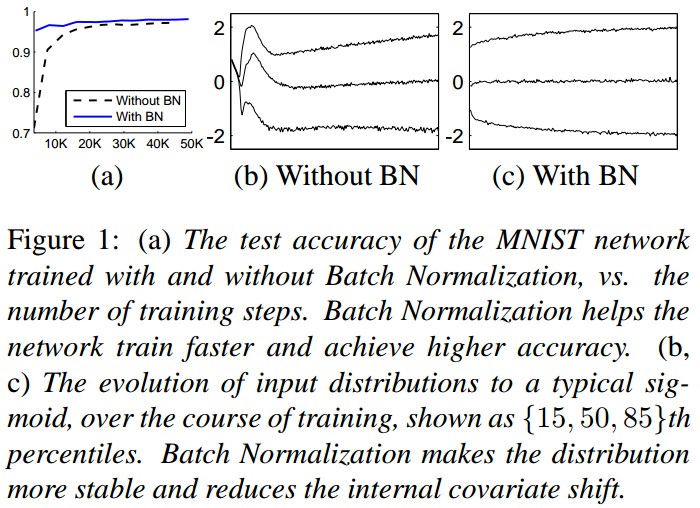
Figure 1. (a) MNIST 网络的测试精度,with BN & without BN. BN层能够更快的训练网络,并取得更高的精度.
(b,c) 可以看出加入 BN 后数据分布更加稳定,减少 internal covariate shift.