题目:Group Normalization - ECCV2018
作者:Yuxin Wu,Kaiming He
团队:FAIR
<Group Normalization for Mask R-CNN - Detectron>
Batch Normalization(BN) 是沿着 batch 维度进行归一化,其受限于 batch size;当 batch size 很小时,BN 会得到不准确的统计估计,会导致模型误差明显增加. 一般每块 GPU 上 batchsize=32 最合适.
但对于目标检测,语义分割,视频场景等,输入图像比较大,而限于显卡显存的限制,导致无法设置较大的 batchsize,如 Mask R-CNN 中,由于图像的分辨率较大,batchsize 只能是 1 或 2.
另一方面,BN 在 batch 维度归一化时,由于 batch 维度并不是固定的,比如,模型训练和测试时的不一致. 往往是在训练集上计算均值(mean) 和方差(variance);而在测试集上直接采用. 如果训练集和测试集的数据分布存在差异时,预训练的均值和方差并不能真实反映测试集.
Group Normalization(GN) 则是提出的一种 BN 的替代方法,其是首先将 channels 划分为多个 groups,再计算每个 group 内的均值和方法,以进行归一化.
GN 的计算与 batchsize 无关,且对于不同的 batchsize ,精度都比较稳定. 另外,GN 易于从 pre-trained 模型进行 fine-tuning.
GN 和 BN 对比如图:
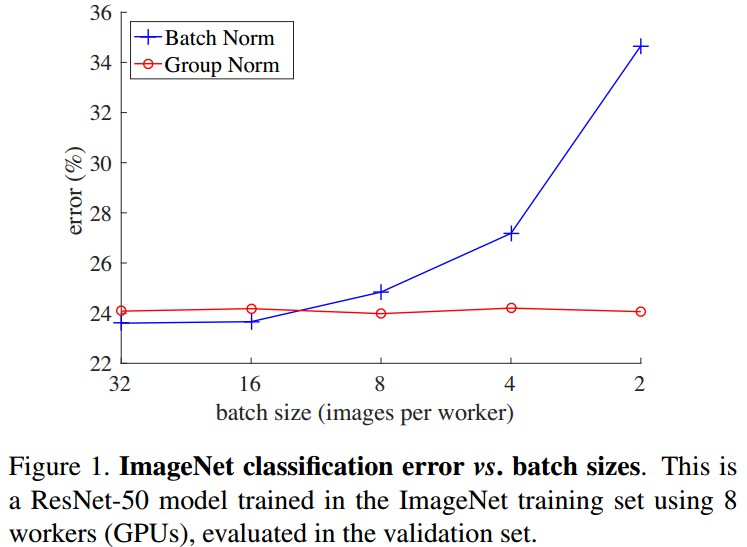
横轴 - 每块 GPU 的 batchsize;纵轴 - 误差率. 在batchsize 较小时,如 batchsize=2, GN 误差率比 BN 小了 10% 左右.
1. GN 数学描述
特征归一化方法:BatchNorm(BN), LayerNorm(LN), InstanceNorm(IN), GroupNorm(GN).
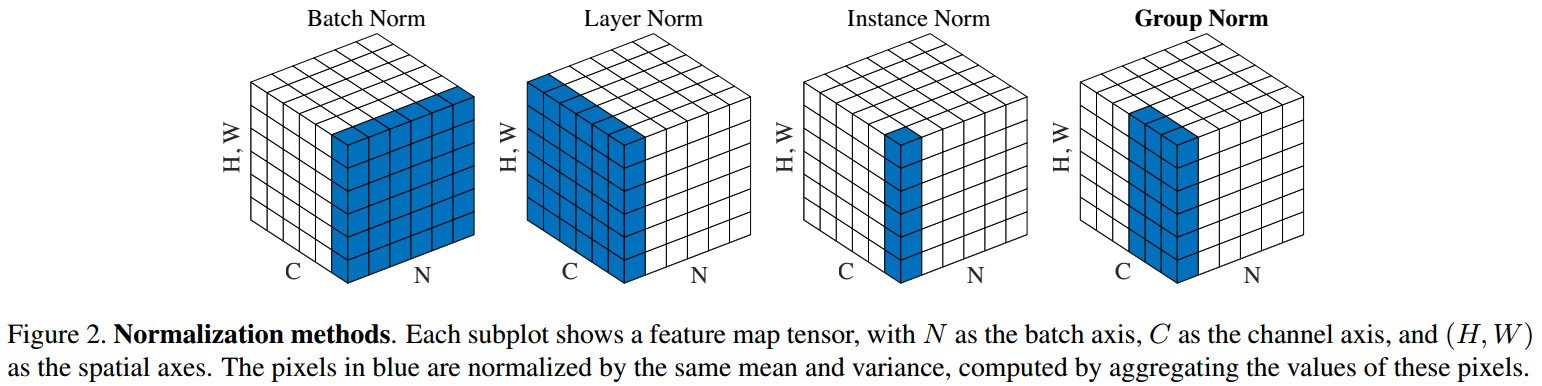
主要解决的问题的数学描述是:
$\hat{x}_i = \frac{1}{\sigma _i}(x_i - \mu _i)$
其中,$x$ 为网络层计算得到的特征;$i$ 是索引(index), 对于 2D 图像,$i = (i_N, i_C, i_H, I_W)$ 是次序为 (N, C,H, W) 的 4D 向量索引;N 是 batch,C 是 channel,H 是空间 height,W 是空间 width.
$\mu$ 是均值,$\mu_i = \frac{1}{m} \sum_{k_i \in \mathcal{S}_i} x_k$
$\sigma$ 是方差,$\sigma_i = \sqrt{\frac{1}{m} \sum_{k\in \mathcal{S}_i} (x_i - \mu_i)^2 + \epsilon}$,$\epsilon$ 为很小的常数.
$\mathcal{S}_i$ 是待计算均值和方差的像素集合. $m$ 是该像素集合的大小.
BN:像素集合 $\mathcal{S}_i = \lbrace k | k_C = i_C \rbrace$. $i_C$ 和 $k_C$ 表示 $i$ 和 $k$ 是沿着 channle 轴 $C$. 也就是说,具有相同 channel 索引的像素进行归一化,如,对于每个 channel,BN 沿着 (N, H, W) 轴计算均值和方差(NxHxW).
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
LN:像素集合 $\mathcal{S}_i = \lbrace k | k_n = i_N \rbrace$,即,LN 对每个样本,沿着 (C, H, W) 计算均值和方差(CxHxW).
torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)
IN:像素集合 $\mathcal{S}_i = \lbrace k | k_n=i_N, k_C=i_C \rbrace$,即,IN对每个样本和每个 channel 通道,沿着 (H, W) 计算均值和方差(HxW).
BN, LN 和 IN 均学习了一个逐通道(per-channel) 的线性变换,以补偿特征表示时可能的信息损失:
$y_i = \gamma \hat{x}_i + \beta$
其中,$\gamma$ 和 $\beta$ 是可训练的 scale 和 shift 参数.
GN:像素集合 $\mathcal{S}_i = \lbrace k | k_N = i_N, [\frac{k_C}{C/G}] = [\frac{i_C}{C/G}] \rbrace$. 其中,G 是 groups 的数量,是预定义的超参数(默认 G = 32.) C/G 是每个 group 内的 channels 通道数. [*] 为取 float 操作. $[\frac{k_C}{C/G}] = [\frac{i_C}{C/G}]$ 表示索引 $i$ 和 $k$ 是相同的 channels 分组 group. GN 对每个 group 内的 C/G 个 channel 通道,沿着(H, W) 计算均值和方差((C/G)xHxW).
如 Figure2 中例示的 GN 计算,是 2 个 groups(G=2),每个 group 有 3 个 channel 的简单例子.
GN 层的计算中,相同 group 内的像素采用相同的均值和方差进行归一化计算.
GN 也学习 per-channel 的 $\gamma$ 和 $\beta$ 参数.
G=C 时,GN 等价于 IN.
G=1 时,GN 等价于 LN.
torch.nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True)
2. GN 实现
GroupNorm Op - group_norm_op.h
2.1 TensorFlow 实现
def GroupNorm(x, gamma, beta, G, eps=1e-5):
# x: 输入特征,shape:[N, C, H, W]
# gamma, beta: scale 和 offset,shape: [1, C, 1, 1]
# G: GN 的 groups 数
N, C, H, W = x.shape
x = tf.reshape(x, [N, G, C//G, H, W])
mean, var = tf.nn.moments(x, [2, 3, 4], keep_dims=True)
x = (x -mean) / tf.sqrt(var + eps)
x = tf.reshape(x, [N, C, H, W])
return x * gamma + beta类似的:
def GroupNorm(x,G=32,eps=1e-5):
N,H,W,C=x.shape
x=tf.reshape(x,[tf.cast(N,tf.int32),
tf.cast(H,tf.int32),
tf.cast(W,tf.int32),
tf.cast(G,tf.int32),
tf.cast(C//G,tf.int32)])
mean,var=tf.nn.moments(x,[1,2,4],keep_dims=True)
x=(x-mean)/tf.sqrt(var+eps)
x=tf.reshape(x,[tf.cast(N,tf.int32),
tf.cast(H,tf.int32),
tf.cast(W,tf.int32),
tf.cast(C,tf.int32)])
gamma = tf.Variable(tf.ones(shape=[1,1,1,tf.cast(C,tf.int32)]), name="gamma")
beta = tf.Variable(tf.zeros(shape=[1,1,1,tf.cast(C,tf.int32)]), name="beta")
return x * gamma + beta2.2 CS231n 作业 - GN 实现
# GN forward
def spatial_groupnorm_forward(x, gamma, beta, G, gn_param):
out, cache = None, None
eps = gn_param.get('eps',1e-5)
N,C,H,W = x.shape
x_group = np.reshape(x, (N, G, C//G, H, W)) #按 G 将C分组
mean = np.mean(x_group, axis=(2,3,4), keepdims=True) #均值
var = np.var(x_group, axis=(2,3,4), keepdims=True) #方差
x_groupnorm = (x_group-mean)/np.sqrt(var+eps) #归一化
x_norm = np.reshape(x_groupnorm, (N,C,H,W)) #还原维度
out = x_norm * gamma + beta # 还原C
cache = (G, x, x_norm, mean, var, beta, gamma, eps)
return out, cache
# GN backward
def spatial_groupnorm_backward(dout, cache):
dx, dgamma, dbeta = None, None, None
N,C,H,W = dout.shape
G, x, x_norm, mean, var, beta, gamma, eps = cache
# dbeta,dgamma
dbeta = np.sum(dout, axis=(0,2,3), keepdims=True)
dgamma = np.sum(dout*x_norm, axis=(0,2,3), keepdims=True)
# 计算dx_group,(N, G, C // G, H, W)
# dx_groupnorm
dx_norm = dout * gamma
dx_groupnorm = dx_norm.reshape((N, G, C // G, H, W))
# dvar
x_group = x.reshape((N, G, C // G, H, W))
dvar = np.sum(dx_groupnorm * -1.0 / 2 * (x_group - mean) / (var + eps) ** (3.0 / 2), axis=(2,3,4), keepdims=True)
# dmean
N_GROUP = C//G*H*W
dmean1 = np.sum(dx_groupnorm * -1.0 / np.sqrt(var + eps), axis=(2,3,4), keepdims=True)
dmean2_var = dvar * -2.0 / N_GROUP * np.sum(x_group - mean, axis=(2,3,4), keepdims=True)
dmean = dmean1 + dmean2_var
# dx_group
dx_group1 = dx_groupnorm * 1.0 / np.sqrt(var + eps)
dx_group2_mean = dmean * 1.0 / N_GROUP
dx_group3_var = dvar * 2.0 / N_GROUP * (x_group - mean)
dx_group = dx_group1 + dx_group2_mean + dx_group3_var
# 还原C得到dx
dx = dx_group.reshape((N, C, H, W))
return dx, dgamma, dbeta3. Results

