论文: Hard-Aware Deeply Cascaded(HDC) Embedding - ICCV2017

作者: Yuhui Yuan, Kuiyuan Yang, Chao Zhang

团队: Peking University, Microsoft Research

实现：[[Code-Caffe]](https://github.com/PkuRainBow/Hard-Aware-Deeply-Cascaded-Embedding_release)

摘要：

深度度量学习基本目标是，使相同类别的图片间的距离比不同类别的图片间的距离小.

由于优化问题，通常采用 hard example mining 来只对样本的 hard 子集进行处理.

但，hard 是相对于模型而言的，复杂模型将大部分样本作为 easy 的，而简单模型将大部分样本作为 hard 的，二者结合又难以训练.

启发点：

样本是具有不同的 hard 层次的，但难以定义复杂性合适的模型，且能充分的选择 hard 样本.

因此，以级联方式来集合不同复杂度的模型，以充分挖掘 hard 样本；通过复杂度递增的一系列模型来判断样本，且只对被判断为 hard 的样本进行模型更新.

实验是将 GoogleNet 的两个辅助 loss 分支和一个主 loss 作为级联模型，三个分支 loss 的权重都设为1，三个分支的特征组合成最终的样本特征.

1.1. 符号说明

[1] - $P = \lbrace I_i^{+}, I_j^{+}\rbrace $，训练数据集构建的全部 positive 图片对，$I_i^{+}$ 和 $I_j^{+}$ 是相同标签(label)或者相似标签的图片；

[2] - $N = \lbrace I_i^{-}, I_j^{-}\rbrace $，训练数据集构建的全部 negative 图片对，$I_i^{-}$ 和 $I_j^{-}$ 是不同标签(label)或者不相关标签的图片；

[3] - $G_k$，第 $k$ 个子网络模块；假设共 $K$ 个网络模块，$G_1$ 的网络输入是图片，而$G_k, k>1$ 的其它模块的输入是前一个模块的输出；$K$ 个网络模块级联地组成前馈网络；$K$ 个模型分别对应 $K$ 个不同深度的子网络；

[4] - $\lbrace o_{i,k}^{+}, o_{j,k}^{+}\rbrace $， 网络 $G_k$ 对于 positive 样本对 $\lbrace I_i^{+}, I_j^{+}\rbrace $ 计算的输出；

[5] - $\lbrace o_{i,k}^{-}, o_{j,k}^{-}\rbrace $， 网络 $G_k$ 对于 negative 样本对 $\lbrace I_i^{-}, I_j^{-}\rbrace $ 计算的输出；

[6] - $F_k$，第 $k$ 个变换函数，将 $o_k$ 转换为低维特征向量 $f_k$，以进行距离计算；

[7] - $\lbrace f_{i,k}^{+}, _{j,k}^{+}\rbrace $，$F_k$ 对于 positive 样本对 $\lbrace I_i^{+}, I_j^{+}\rbrace $ 计算的第 $k$ 个特征向量；

[8] - $\lbrace f_{i,k}^{-}, _{j,k}^{-}\rbrace $，$F_k$ 对于 negative 样本对 $\lbrace I_i^{-}, I_j^{-}\rbrace $ 计算的第 $k$ 个特征向量；

1.2. HDC 框架图

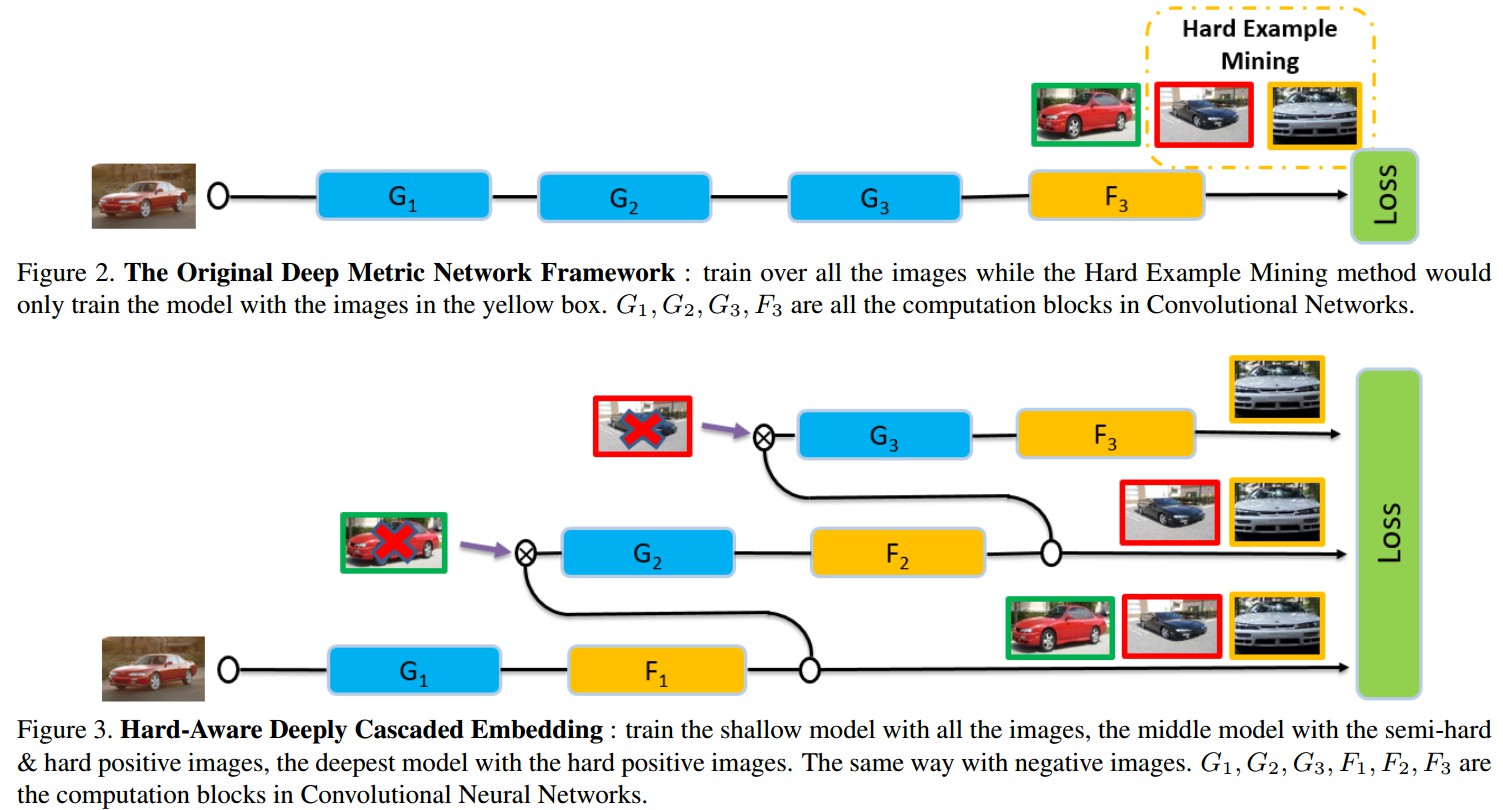
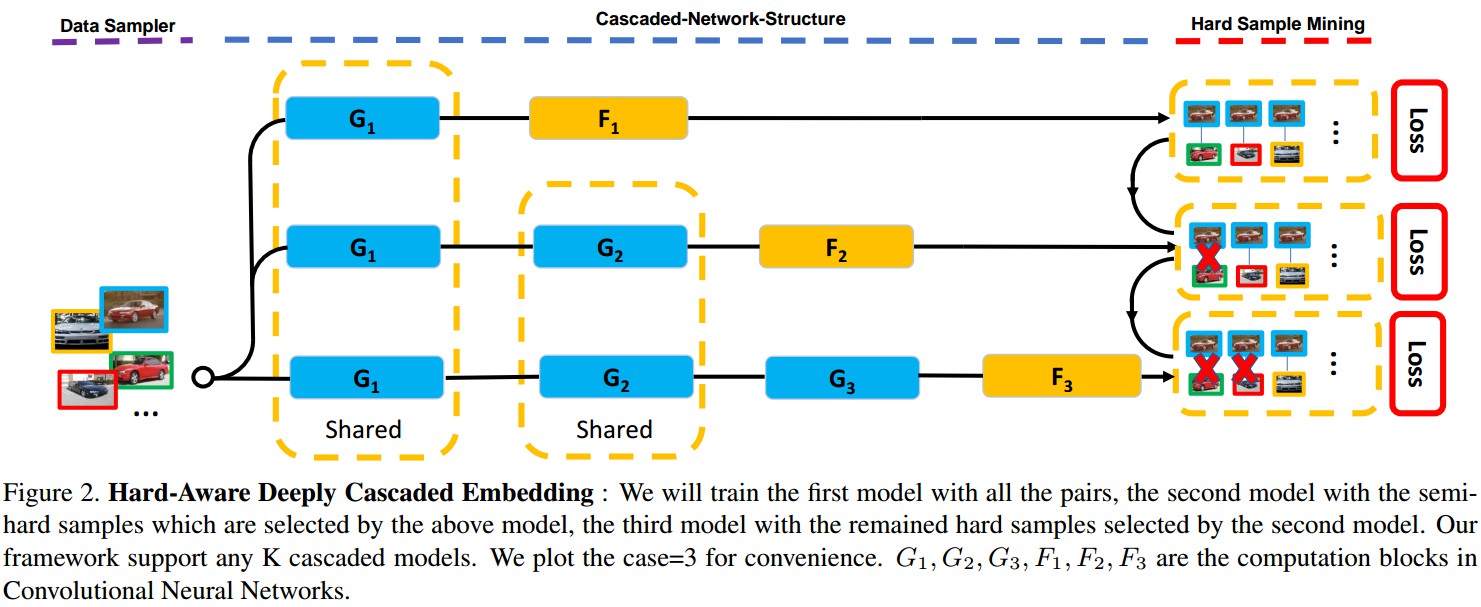
Figure 2. HDC Embedding. 对所有的样本对训练模型 $G_1$，基于模型 $G_1$ 选择的 semi-hard samples 训练模型 $G_2$，基于模型 $G_2$ 选择的剩余的 hard samples 训练模型 $G_3$. $F_1, F_2, F_3$ 分别为 $G_1, G_2, G_3$ 的特征变换.

1.2.1. 前向计算

前向计算:

第一个网络模块 $G_1(k=1)$:

$$ \lbrace o_{i, 1}, o_{j, 1}\rbrace = G_1 \circ \lbrace I_i, I_j\rbrace $$

$$ \lbrace f_{i,1}, f_{j,1}\rbrace = F_1 \circ \lbrace o_{i, 1}, o_{j, 1}\rbrace $$

其是对于样本对 $\lbrace I_i, I_j\rbrace $ 计算得到的特征.

第 $k$ 个网络模块 $G_k(1<k<K)$:

$$ \lbrace o_{i, k}, o_{j, k}\rbrace = G_k \circ \lbrace o_{i, k-1}, o_{j, k-1}\rbrace $$

$$ \lbrace f_{i,k}, f_{j, k}\rbrace = F_k \circ \lbrace o_{i, k}, o_{j, k}\rbrace $$

其是网络 $G_k$ 计算得到的特征

​

第 $k$ 个网络模块的 Loss 函数：

$$ L_k = \sum _{(i, j) \in P_k} L_{k}^{+}(i, j) + \sum _{(i, j) \in N_k} L_{k}^{-}(i, j) $$

其中，$P_k$，被先前模型判定为 hard examples 的所有 positive 样本对；$N_k$，被先前模型判定为 hard examples 的所有 negative 样本对.

HDC 的最终 Loss 函数：

$$ L = \sum_{k=1} ^{K} \lambda_k L_k $$

其中，$\lambda _k$ - 权重

1.2.2. 梯度计算

梯度计算：

采用 SGD 优化，

Loss 关于模型 $G_k$ 的梯度计算：

$$ \frac{\partial {L} }{\partial{G_k} } = \sum_{l=k}^K \lambda_l \frac{\partial{L_l}}{\partial{G_k}} $$

其中，$G_k$ 的梯度计算需要对所有 $G_k$ 相关的模型

Loss 关于变换 $F_k$ 的梯度计算：

$$ \frac{\partial {L} }{\partial{F_k} } =\lambda_k \frac{\partial{L_l}}{\partial{F_k}} $$

其中，$F_k$ 的梯度计算只需对模型 $k$，因为只对模型 $k$ 进行了特征变换.

1.2.3. 对比损失

loss 函数- contrastive loss

Contrastive Loss 是使 positive 样本对和距离小于边缘参数的 negative 样本对间的距离尽可能大.

$$ L^{+}(i, j) = D(f_i^{+}, f_j^{+}) $$

$$ L^{-}(i, j) = max\lbrace 0, M - D(f_i^{-}, f_j^{-})\rbrace $$

其中，

$D(f_i, f_j)$ - 两个 L2-normalized 特征向量 $f_i$ 和 $f_j$ 间的 Euclidean 距离.

$M$ - 边缘参数(margin)

因此，基于 Contrastive Loss 的 HDC Loss 函数为：

$$ L_k = \sum_{(i,j) \in P_k} D(f_{i, k}^{+}, f_{j, k}^{+}) + \sum_{(i, j)\in N_k)} max\lbrace 0, M - D (f_{i, k}^{-}, f_{j, k}^{-})\rbrace $$

1.3. Hard Example 的选择

给定 loss 函数，可以根据传统的 hard example mining 方法来定义 loss 值较大的样本作为 hard examples，但多个 loss 值将被用于挖掘每一个样本的 hard examples.

由于不同模型的 loss 分布是不同的，且在训练过程中一直变化，因此在挖掘 hard examples 时，很难预定义每个模型的阈值.

这里采用一种简单的处理方式：

以降序方式对 mini-batch 内的所有的 positive 样本对的 losses 进行排列；然后取前 $h^k$ 比例的样本作为模型 $k$ 的 hard positive set；

类似地，

以降序方式对 mini-batch 内的所有的 negative 样本对的 losses 进行排列；然后取前 $h^k$ 比例的样本作为模型 $k$ 的 hard negative set；

被选取的 hard samples 传向后面的级联网络模型.

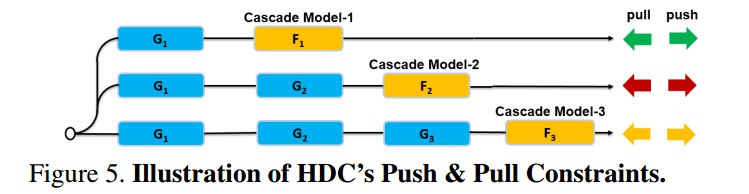
例示：

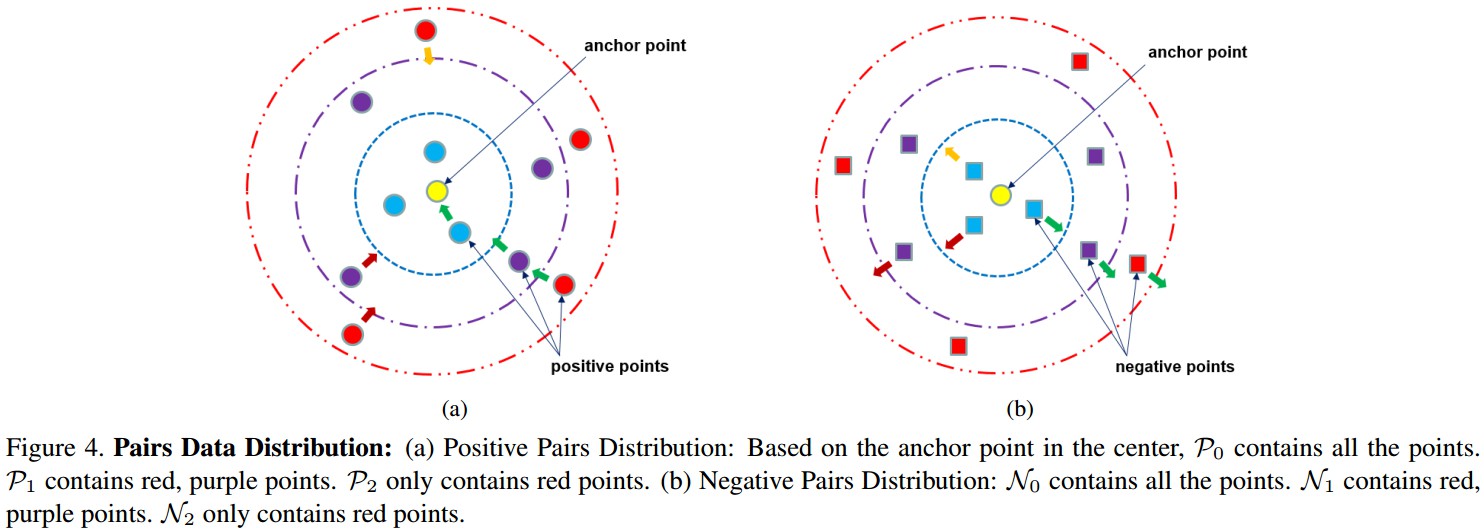
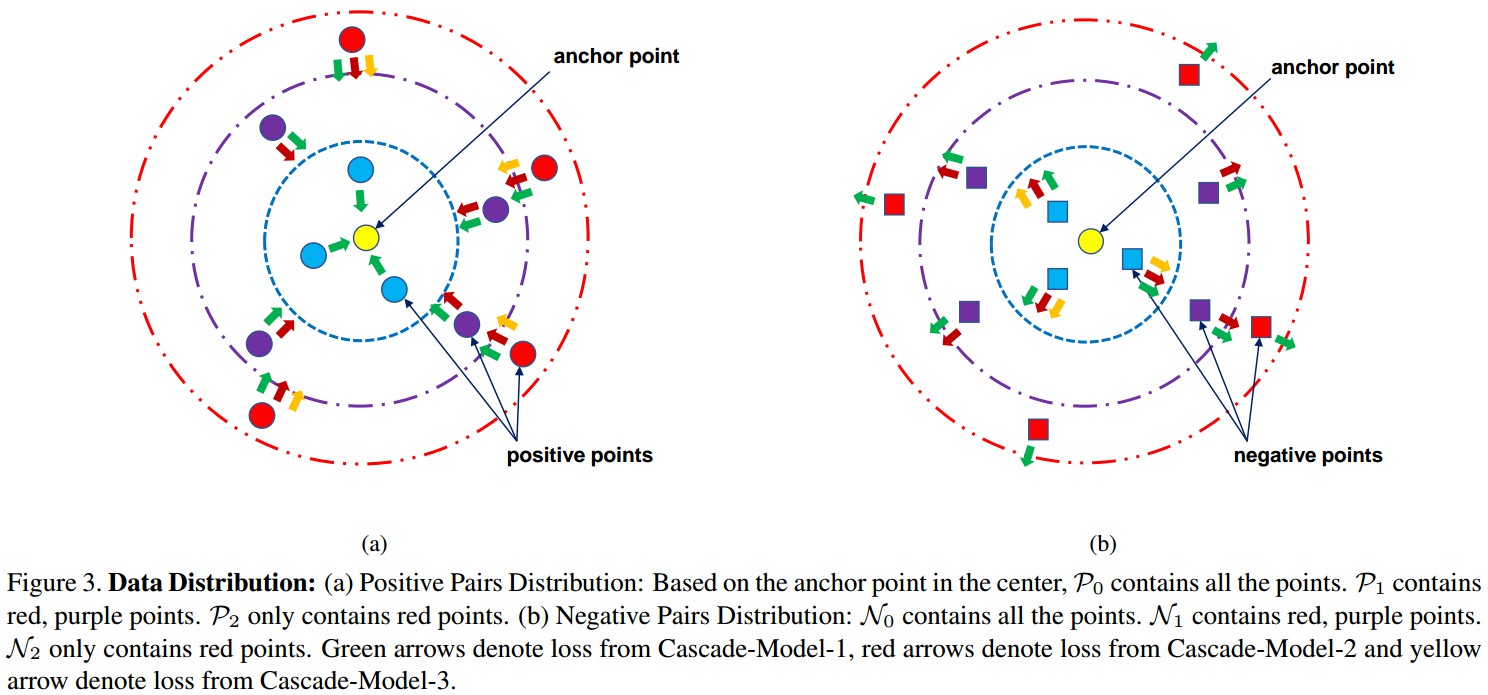
Figure 3. 数据分布.

[1] - Positive 样本对分布：基于中心的 anchor 点，$P_0$ 包含所有的点，$P_1$ 包含红色、紫色的点，$P_2$ 只包含红色的点.

[2] - Negative 样本对分布： $N_0$ 包含所有的点，$N_1$ 包含红色、紫色的点；$N_2$ 只包含红色的点.

绿色箭头表示 Cascade-Model-1 的 loss，红色箭头表示 Cascade-Model-2 的 loss，黄色箭头表示 Cascade-Model-3 的 loss.

Cascade-Model-1 对 $P_0$ 和 $N_0$ 的所有样本对进行 forward，并尝试将所有的 positive 点 push 靠近到 anchor 点，同时将所有的 negative 点 push 远离 anchor 点； 根据 loss 值选择 hard samples，形成 $P_1$ 和 $N_1$(即，第2个和第3个虚线圆内的点). 类似地， Cascade-Model-2 得到 $P_2$ 和 $N_2$(即，第3个虚线圆内的点).

1.4 HDC 实现细节

类似于 lifted structured feature embedding ，构建图像 mini-batch 作为输入，例如，一个 mini-batch 内的 100 张图片是均匀地从 10 个不同的类别中随机采样得到的.

为了利用更多训练样本，采用[Learning a metric embedding for face recognition using the multibatch method]() 的 mini-batch 方法，构建 min-batch 内的所有图像对，以计算训练 loss；例如，一个 mini-batch 内有 100 张图片，可以构建 $100^2 - 100 = 9900$ 个图像对.

基于 HDC 级联模型，一张图片是由全部模型的链接特征来表示的.

算法：

[1] - 输入： 训练数据集 $\lbrace I_i\rbrace _{i=1}^N$

[2] - for $t = 1; t < N; t++$ do

[3] - xxxx 根据类似于 lifted structured feature embedding 的方法，采样 mini-batch 的训练图片；并根据[Learning a metric embedding for face recognition using the multibatch method]() 的方法对 mini-batch 内的训练图片初始化 $P_0$ 和 $N_0$.

[4]- xxxx for $k = 1; k \leq K; k++$ do

[5] - xxxxxxxx 对样本集 $P_{k-1}$ 和 $N_{k-1}$ 内的所有图片进行 forward 到第 $k$ 个模型，以根据下面公式计算特征：

$\lbrace o_{i, k}, o_{j, k}\rbrace = G_k \circ \lbrace o_{i, k-1}, o_{j, k-1}\rbrace $

$\lbrace f_{i,k}, f_{j, k}\rbrace = F_k \circ \lbrace o_{i, k}, o_{j, k}\rbrace $

网络 $G_k$ 计算得到的特征

[6] - xxxxxxxx 根据下面的公式，计算 mini-batch 内全部样本对的losses：

$L^{+}(i, j) = D(f_i^{+}, f_j^{+})$

$L^{-}(i, j) = max\lbrace 0, M - D(f_i^{-}, f_j^{-})\rbrace $

[7] - xxxxxxxx 根据 1.3 中 hard examples 选择方法，选择 hard 样本对，得到 $P_k$ 和 $N_k$.

[8] - xxxxxxxx 根据梯度计算公式，对 $P_k$ 和 $N_k$ 内的所有样本对进行 backward 和更新：

$ \frac{\partial {L} }{\partial{G_k} } = \sum_{l=k}^K \lambda_l \frac{\partial{L_l}}{\partial{G_k}}$

$\frac{\partial {L} }{\partial{F_k} } =\lambda_k \frac{\partial{L_l}}{\partial{F_k}} $

[9] - xxxx end for

[10] - end for

2. Experiments

HDC - image-retrieval tasks.

[1] - CARS196 dataset

196 类 cars，16185 张图片，前 98 类(8054张图片)作训练，其余 98 类(8131张图片) 作测试.

[2] - CUB-200-2011 dataset

200 类 birds，11788 张图片，前 100 类(5864 张图片)作训练，其余的(5924 张图片) 作测试.

[3] - Stanford Online Products dataset

22634 类 products，120053 张图片，11318 类(59551 张图片) 作训练，其余的 11316 类(共 60502 张图片)作测试.

[4] - In-shop Clothes Retrieval dataset
DeepFashion，11735 类 clothes，54642 张图片，从中筛选 7982 类(52712 张图片) 作训练和测试. 3997 类(25882 张图片)作训练，3985类(28760 张图片)作测试.
测试集分为 query set 和 database set. query set 共 3985 类(14218 张图片)；database set 共 3985 类(12612 张图片).

[5] - VehicleID dataset

26267 类 vehicles，221763 张图片，13134 类(110178 张图片)作训练，13133 类(111585 张图片)作测试.

2.1. SetUp

基于 GoogleNet. $K = 3$，$\lambda_1 = \lambda_2 = \lambda_3 = 1$，$\lbrace h^1, h^2, h^3\rbrace = \lbrace 100, 50, 20\rbrace $，mini-batch=100，边缘参数 $M=1$，初始 learning rate = 0.01，每 3-5 epoches $×10$，网络训练 15 epoches. HDC 的各级联模型的 embedding dimensions = 128，最终的 feature dimension = 384.

2.2. Results