原文:研究|数据预处理|归一化 (标准化)
数据预处理在众多深度学习算法中都起着重要作用,实际情况中,将数据做归一化和白化处理后,很多算法能够发挥最佳效果.
然而除非对这些算法有丰富的使用经验,否则预处理的精确参数并非显而易见.
1. 数据归一化及其应用
数据预处理中,标准的第一步是数据归一化.
虽然这里有一系列可行的方法,但是这一步通常是根据数据的具体情况而明确选择的.
特征归一化常用的方法包含如下几种:
- 简单缩放
- 逐样本均值消减(也称为移除直流分量)
- 特征标准化(使数据集中所有特征都具有零均值和单位方差)
一般做机器学习应用的时候大部分时间是花费在特征处理上,其中很关键的一步就是对特征数据进行归一化,为什么要归一化呢?很多同学并未搞清楚,维基百科给出的解释:
- 归一化后加快了梯度下降求最优解的速度;
- 归一化有可能提高精度;
加快梯度下降求解速度
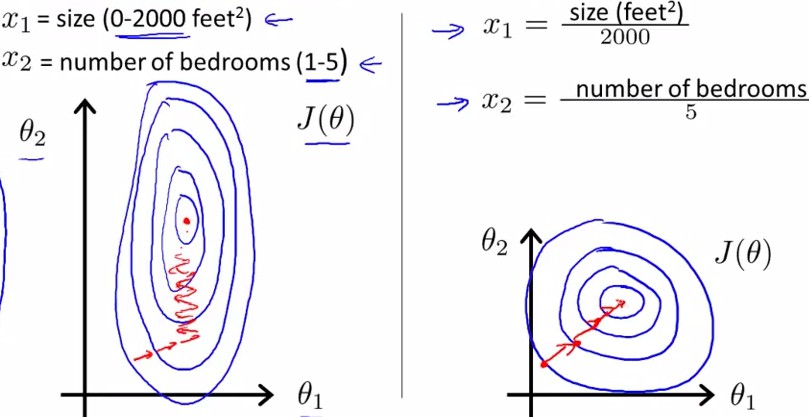
如下图所示,蓝色的圈圈图代表的是两个特征的等高线.
其中左图两个特征 X1 和 X2 的区间相差非常大,X1区间是[0, 2000],X2区间是[1,5],其所形成的等高线非常尖.当使用梯度下降法寻求最优解时,很有可能走“之字型”路线(垂直等高线走),从而导致需要迭代很多次才能收敛;
而右图对两个原始特征进行了归一化,其对应的等高线显得很圆,在梯度下降进行求解时能较快的收敛.
因此如果机器学习模型使用梯度下降法求最优解时,归一化往往非常有必要,否则很难收敛甚至不能收敛.
归一化有可能提高精度
一些分类器需要计算样本之间的距离(如欧氏距离),例如KNN。如果一个特征值域范围非常大,那么距离计算就主要取决于这个特征,从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要).
简单缩放 | min-max标准化(Min-max normalization) | 离差标准化
在简单缩放中,目的是通过对数据的每一个维度的值进行重新调节(这些维度可能是相互独立的),使得最终的数据向量落在 [0, 1] 或 [ − 1, 1] 的区间内(根据数据情况而定). 这对后续的处理十分重要,因为很多默认参数(如 PCA-白化中的 epsilon) 都假定数据已被缩放到合理区间.
例如:在处理自然图像时,获得的像素值在 [0,255] 区间中,常用的处理是将这些像素值除以 255,使它们缩放到 [0,1] 中.
这种算法是对原始数据的线性变换,使结果落到 [0, 1] 区间,转换函数如下:
x = (x - min)/(max - min)
max: 样本数据的最大值
min: 为样本数据的最小值
适用场景
这种归一化方法比较适用在数值比较集中的情况.
但是,如果max和min不稳定,很容易使得归一化结果不稳定,使得后续使用效果也不稳定,实际使用中可以用经验常量值来替代max和min. 而且当有新数据加入时,可能导致max和min的变化,需要重新定义.
在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用第一种方法或其他归一化方法. 比如图像处理中,将RGB图像转换为灰度图像后将其值限定在 [0 255] 的范围.
标准差标准化 | z-score 0均值标准化(zero-mean normalization)
经过处理的数据符合标准正态分布,即均值为 0,标准差为 1,其转化函数为:
x = (x - u)/σ
u: 所有样本数据的均值
σ: 为所有样本数据的标准差.
在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,第二种方法(Z-score standardization)表现更好.
归一化
import numpy as np
X-=np.mean(X, axis=0) # X 的每一列都减去该列的均值
X/=numpy.std(X,axis=0) # 数据归一化
白化
import numpy as np
X -= np.mean(X, axis=0) # 将数据零均值化
cov = np.dot(X.T, X)/X.shape[0] #计算协方差矩阵
# 去相关操作,
# 即通过将原始数据(零均值化后的数据)投影到特征基空间(eigenbasis)
U, S, V = np.linalg.svd(cov) # 计算数据协方差矩阵的奇异值SVD分解
Xrot = np.dot(X, U) # 对数据去相关
# 白化处理,
# 即把特征基空间的数据除以每个维度的特征值来标准化尺度.
Xwhite = Xrot/np.sqrt(S+1e-5) #除以奇异值的平方根,1e-5 防止分母为 0.
PCA 白化的一个缺点是会增加数据中的噪声.
因为它把输入数据的所有维度都延伸到相同的大小,这些维度中就包含噪音维度(往往表现为不相关的且方差较小).
这种缺点在实际操作中可以通过把1e-5增大到一个更大的值来引入更强的平滑.
非线性归一化
经常用在数据分化比较大的场景,有些数值很大,有些很小.
通过一些数学函数,将原始值进行映射.
该方法包括 log、指数,正切等。需要根据数据分布的情况,决定非线性函数的曲线,比如 log(V, 2) 还是 log(V, 10)等.
参考
[1] - 数据预处理
[2] - 数据的标准化
[3] - 为什么一些机器学习模型需要对数据进行归一化
[4] - 再谈机器学习中的归一化方法(Normalization Method)
[5] - sklearn scaler
[6] - sklearn scaler 2
[7] - 关于使用sklearn进行数据预处理 —— 归一化/标准化/正则化
[8] - 深度神经网络训练的必知技巧