GPU 优化简介 原文 - An Introduction to GPU Optimization

采用 GPUs 加速简单的计算任务.

计算机处理的很多任务都会遇到大量的计算，耗时较多的问题；而且，随着数据集越来越大，耗时将更多. 解决方法之一是，使用线程(threads).

这里简单介绍 GPU 加速的工作模式，并通过 GPU 任务的一个简单 API 代码来说明其加速效果.

首先，看一个矩阵相乘的例子.

<h2>矩阵乘法 Matrix Multiplication</h2>


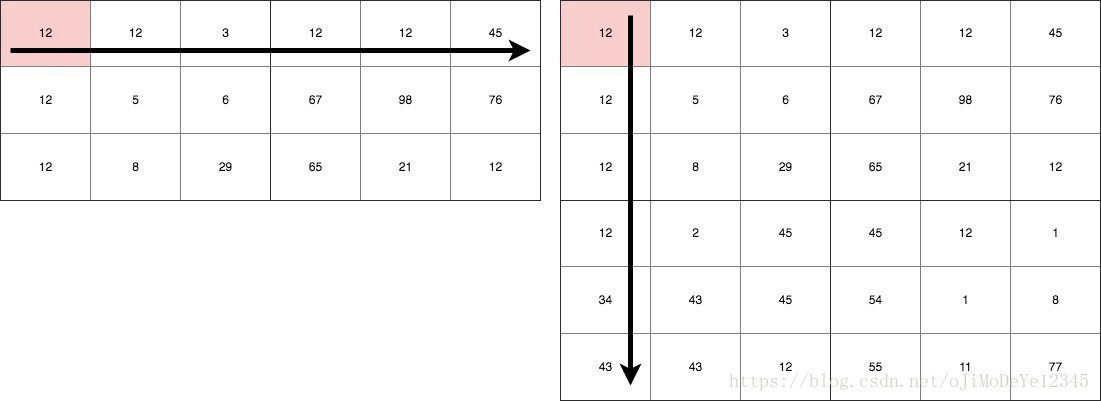
Figure 1. 矩阵乘法

假设有两个矩阵，其大小分别为：3 × 6 和 6 × 6. 两矩阵相乘得到的结果矩阵大小为 3 × 6. 结果矩阵的每个单元 cell 都有 6 次计算，因此，共有 3 × 6 × 6 次乘法计算.

即：计算的时间复杂度为 ${ O(mn^2) }$.

意味着，对于一个大小为 2000 × 2000 的矩阵而言，将进行的计算会达到 8, 000, 000, 000 次，会耗费 CPU 大量的时间！

<h2>GPUs 简介</h2>

GPUs 通常包含大量的处理核心(processing cores). 数量一般从 384 到上千个. 如图，NVIDIA 的部分显卡 GPUs.


Figure 2. NVIDIA GPUs CUDA 核心数

CUDA，Compute Unified Device Architecture. 其运行速度运行相对较慢，但通过利用大量的ALUs(Arithmetic and Logical Units)，具有强大的并行化能力. 可参见 WHAT IS GPU-ACCELERATED COMPUTING?


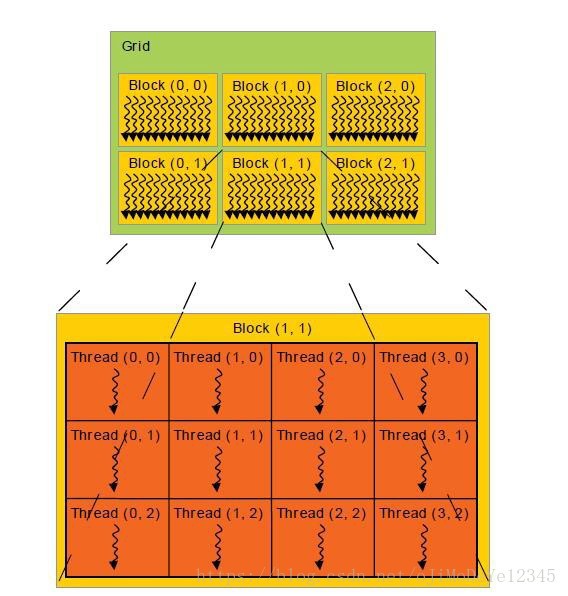
Figure 3. CUDA Thread Model

上图给出了 CUDA 的线程模型(AMD 也是差不多相同的结构).

为了便于说明，假设每个 CUDA 核心或一个 GPU 核心一次运行一个线程 thread. 如果数据集很大时，可以对数据集进行分片 pieces. 一个 方格Grid 包含多个 块 Blocks，Block 是一个矩阵，由与其大小相同数量的 线程 Threads 组成.

这里采用一个简单的 JAVA API 来说明 FIgure 3.

<h2>关于 GPU 的思考</h2>

正如前面所说，每个 GPU 核心能够运行分离的线程.

这里可以假设，矩阵的每个单元 cell 可以通过一个单独的 GPU 核心来计算. 而且，由于所有的核心是并行化运行的，那么所有的矩阵单元也可以并行化计算. 因此，计算的时间复杂度降到了 O(n).

一个 2000 × 2000 的矩阵乘法，只需要 2000 次运行，对于计算机而言是很轻松的.

每一个线程thread，都有唯一的身份，即，线程在 Block 和 Grid 的位置. 也就是矩阵的单元所在位置.

另外，矩阵是加载在 GPU 的共享内存里的，可以根据其索引直接读取矩阵的单元数据，以并行化计算.

很简单吧，下面通过代码来说明.

<h2>基于 APARAPI 的 GPU 编程</h2>

APARAPI (A-PARallel-API) 是 OpenCL 的 JAVA 接口，是用于 GPUs 编程的开放式计算语言，其支持 CUDA 结构和 AMD 设备.

  • pom.xml 
    <?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"
       xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
       xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
  <modelVersion>4.0.0</modelVersion>

  <groupId>cuda-aparapi</groupId>
  <artifactId>cuda</artifactId>
  <version>1.0-SNAPSHOT</version>

  <dependencies>
      <dependency>
          <groupId>com.aparapi</groupId>
          <artifactId>aparapi</artifactId>
          <version>1.4.1</version>
      </dependency>
  </dependencies>


</project>
    </li> <li>MatrixMultiplication.java 
    import com.aparapi.Kernel;
import com.aparapi.Range;

/**
* Created by anuradhawick on 12/29/17.
*/
public class MatrixMultiplication {

  public static void main(String[] args) {
      // Width of the matrix
      final int SIZE = 5000;

      // We should use linear arrays as supported by the API
      final int[] a = new int[SIZE * SIZE];
      final int[] b = new int[SIZE * SIZE];
      int[] c = new int[SIZE * SIZE];
      final int[] d = new int[SIZE * SIZE];
      int val;

      // Creating random matrices
      for (int i = 0; i < SIZE; i++) {
          for (int j = 0; j < SIZE; j++) {
              a[i  SIZE + j] = (int) (Math.random()  100);
              b[i  SIZE + j] = (int) (Math.random()  100);
          }
      }
      long time = System.currentTimeMillis();

      // CPU multiplication
      System.out.println("Starting single threaded computation");
      for (int i = 0; i < SIZE; i++) {
          for (int j = 0; j < SIZE; j++) {
              val = 0;
              for (int k = 0; k < SIZE; k++) {
                  val += a[i  SIZE + k]  b[k * SIZE + j];
              }
              c[i * SIZE + j] = val;
          }
      }
      System.out.println("Task finished in " + (System.currentTimeMillis() - time) + "ms");

      // Kernel for multiplication
      Kernel kernel = new Kernel() {
          @Override
          public void run() {
              int row = getGlobalId() / SIZE;
              int col = getGlobalId() % SIZE;
              if (row > SIZE || col > SIZE) return;

              d[row * SIZE + col] = 0;

              for (int i = 0; i < SIZE; i++) {
                  d[row  SIZE + col] += a[row  SIZE + i]  b[i  SIZE + col];
              }
          }
      };

      // Array size for GPU to know
      Range range = Range.create(SIZE * SIZE);

      System.out.println("Starting GPU computation");
      time = System.currentTimeMillis();
      kernel.execute(range); // Running the Kernel
      System.out.println("Task finished in " + (System.currentTimeMillis() - time) + "ms");

      // Verifying the result
      for (int i = 0; i < SIZE; i++) {
          for (int j = 0; j < SIZE; j++) {
              if (c[i  SIZE + j] != d[i  SIZE + j]) {
                  System.out.println("ERROR");
                  return;
              }
          }
      }
  }
}
    </li> </ul> 核Kernel是 GPU 执行代码的一部分， Kernel 可见的变量被复制到 GPU RAM. 以上代码中，GPUs 组织数据的形式是线性数组(linear array)，而非 2D 数组的形式. 虽然，GPUs 不能处理 2D 数组，但其数据处理方式类似于数组维度. 
    Range range = Range.create(SIZE * SIZE);

    分配 GPU 内存，GPU 最多会运行 SIZE × SIZE 个线程.

    int row = getGlobalId() / SIZE;
int col = getGlobalId() % SIZE;

    从线程的专有内存(private memory) 获取线程 Id. 根据 Id 即可确定线程的单元格位置.

    对于每个单元格，计算

    for (int i = 0; i < SIZE; i++) {
    d[row  SIZE + col] += a[row  SIZE + i]  b[i  SIZE + col];
}

    仅仅是对两个矩阵对应单元格的计算结果进行相加.

    只需采用线程索引定义单个线程的 Kernel. 所有线程并行化运行.

    GPU 计算的速度会有多快呢，以上代码的输出为：

    // 1200 x 1200
Starting single threaded computation
Task finished in 25269ms 
Starting GPU computation
Task finished in 1535ms

    相差很大！

    由于 CPU 耗时较久，以下仅为 GPU 计算耗时：

    // 2000 x 2000 
Task finished in 3757ms
// 5000 x 5000 
Task finished in 5402ms

    <h2>Related</h2>

    [1] - GPU Optimized dynamic programming

Last modification：October 10th, 2018 at 04:13 pm
© 允许规范转载