原文：Unsupervised Learning with Python - 2018.05.12

作者：Vihar Kurama

无监督学习是机器学习技术的一类，其用于发现数据中的模式(patterns). 无监督算法的输入数据是无标签、未手工标注的，也就是说，对于无监督算法，其只需提供输入变量(X)，而无需提供对应的输入变量(标签数据). 无监督学习算法自己去挖掘数据中有意义的结构信息.

Yan Lecun, director of AI research, explains that unsupervised learning —teaching machines to learn for themselves without having to be explicitly told if everything they do is right or wrong — is the key to “true” AI.

1. 监督学习与无监督学习

监督学习中，系统尝试从之前给出的例子中进行学习. 而，无监督学习中，系统尝试直接从给出的例子进行学习.

因此，如果数据集没有标签数据，那么其是一个无监督问题.

image

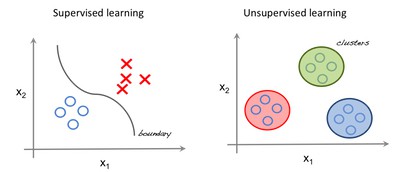
From [http://beta.cambridgespark.com/courses/jpm/01-module.html]

如上如，左图是监督学习，可以使用回归技术寻找特征之间的最佳拟合；右图是无监督学习，输入是特征分离的，预测是基于其归属的聚类进行的.

重要术语:

  • 特征(Feature)：用于进行预测的输入变量.
  • 预测(Predictions)：对于输入样本，模型预测的输出.
  • 样本(Example)：数据集的一行. 一个样本包含一个或多个特征，可能包含标签.
  • 标签(Label)：特征的结果.

2. 无监督学习的数据准备

这里采用 Iris (鸢尾花卉)数据集 为例. 该数据集包含 150 个记录样本集，有 5 个属性 - 花瓣长度(Petal Length)，花瓣宽度(Petal Width)，萼片长度(Sepal Length)，萼片宽度(Sepal Width)和类别(Class). 类别包含三个：山鸢尾(Iris Setosa)，维吉尼亚鸢尾(Iris Virginica) 和变色鸢尾(Iris Versicolor).

对于无监督学习算法，给出的鸢尾花的这四个特征， 并进行预测其类别.

这里采用 Python scikit-learn 库和 matplotlib 可视化库.

from sklearn import datasets
import matplotlib.pyplot as plt

# Loading dataset
iris_df = datasets.load_iris()

# Available methods on dataset
print(dir(iris_df))

# Features
print(iris_df.feature_names)

# Targets
print(iris_df.target)

# Target Names
print(iris_df.target_names)
label = {0: 'red', 1: 'blue', 2: 'green'}

# Dataset Slicing
x_axis = iris_df.data[:, 0]  # Sepal Length
y_axis = iris_df.data[:, 2]  # Sepal Width

# Plotting
plt.scatter(x_axis, y_axis, c=iris_df.target)
plt.show()

输入如：

['DESCR', 'data', 'feature_names', 'target', 'target_names']
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
['setosa' 'versicolor' 'virginica']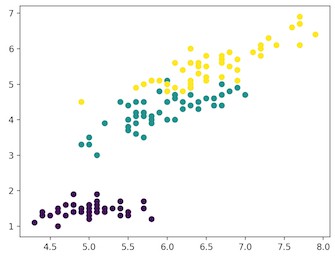

image

图1. 紫色：山鸢尾；绿色：维吉尼亚鸢尾；黄色：变色鸢尾

3. 聚类(Clustering)

聚类问题中，数据被分成几个组. 简单地说，其目的是将具有相似特征的组分开，并将特征组成聚类.

如图：

image

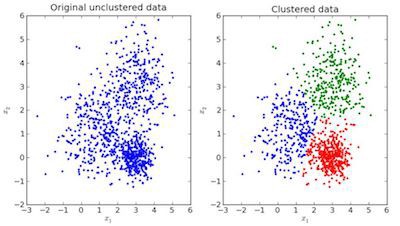
图 2. 聚类示例.

如上图中，左图为原始数据；右图为聚类结果(根据数据的特征聚类). 当给定输入样本时，根据其特征，检测其特征所归属的聚类，进行预测.

3.1. KMeans 聚类

K-Means 是一种迭代聚类算法(iterative clustering algorithm)，其旨在，在每次迭代中寻找局部最大值.

首先，需要给出初始化聚类数. 这里，由于已知数据集包含 3 个类别，因此，设置初始化聚类数量为 3，即 n_clusters=3.

然后，随机选择三个点(输入) 作为三个聚类(聚类中心). 基于各数据点之间的质心距离(centroid distance)，判定下一个给定输入被分到的聚类；

接着，重新计算所有聚类的质心.

每个聚类的质心是特征值的集合，其定义了聚类生成的分组. 根据质心特征权重，可以定性地解释每个聚类所代表的分组类型.

基于 skearn 库的 KMeans 模型，拟合特征并进行预测.

from sklearn import datasets
from sklearn.cluster import KMeans

# Loading dataset
iris_df = datasets.load_iris()

# Declaring Model
model = KMeans(n_clusters=3)

# Fitting Model
model.fit(iris_df.data)

# Predicitng a single input
predicted_label = model.predict([[7.2, 3.5, 0.8, 1.6]])

# Prediction on the entire data
all_predictions = model.predict(iris_df.data)

# Printing Predictions
print(predicted_label)
print(all_predictions)

输出如下：

[0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 
2 1 1 1 1 2 1 1 1 1 1 1 2 2 1 1 1 1 2 1 2 1 2 1 1 2 2 1 1 1 1 1 2 1 1 1 1 2 1 1 1 2 1 1 1 2 1 1 2]

3.2. 分层聚类(Hierarchical Clustering)

分层聚类，顾名思义，是一种构建聚类层次的算法. 该算法首先从分配给自己一个聚类的所有数据开始. 然后，将最相近的两个聚类合并为同一个聚类. 最后，只剩下一个聚类时，结束算法.

分层聚类可以采用树状图(dendrogram) 进行表示.

from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
import pandas as pd

# Reading the DataFrame
seeds_df = pd.read_csv(
    "https://raw.githubusercontent.com/vihar/unsupervised-learning-with-python/master/seeds-less-rows.csv")

# Remove the grain species from the DataFrame, save for later
varieties = list(seeds_df.pop('grain_variety'))

# Extract the measurements as a NumPy array
samples = seeds_df.values

"""
Perform hierarchical clustering on samples using the
linkage() function with the method='complete' keyword argument.
Assign the result to mergings.
"""
mergings = linkage(samples, method='complete')

"""
Plot a dendrogram using the dendrogram() function on mergings,
specifying the keyword arguments labels=varieties, leaf_rotation=90,
and leaf_font_size=6.
"""
dendrogram(mergings,
           labels=varieties,
           leaf_rotation=90,
           leaf_font_size=6,
           )

plt.show()

如图：

image

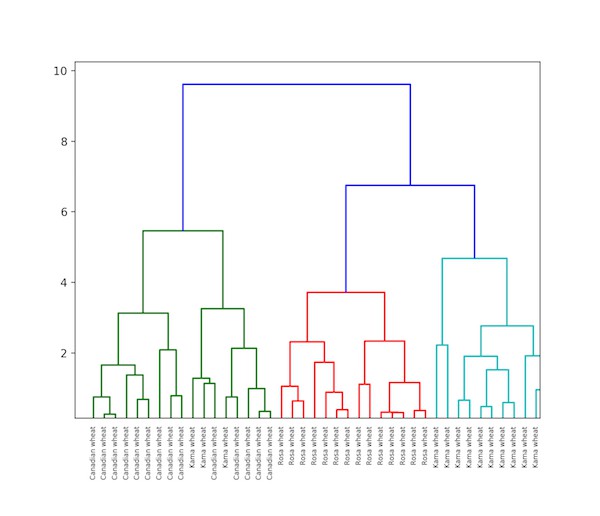
3.3. KMeans 聚类与分层聚类的区别

[1] - 分层聚类不能很好地处理大数据，但 KMeans聚类可以.

因为 KMeans 的时间复杂度是线性的，即O(n)，而分层聚类的时间复杂度是二次的，即O(n2).

[2] - KMeans 聚类，采用随机初始化聚类中心，多次运行算法产生的结果可能会有所不同. 但分层聚类可以重现聚类结果.

[3] - 当聚类的形状是超球形时(如2D中的圆形，3D中的球形)，KMeans 聚类更好.

[4] - KMeans 聚类不允许嘈杂的数据，而分层聚类可以直接使用嘈杂的数据集进行聚类.

3.4. t-SNE 聚类

t-SNE 聚类是用于可视化的无监督学习方法之一.

t-SNE 表示 t分布的随机近邻嵌入(t-distributed stochastic neighbor embedding).

t-SNE 将高维空间映射到可以可视化的2或3维空间.

具体而言，t-SNE 算法通过二维点或三维点对每个高维对象进行建模，使得相似样本由附近的点建模，而不相似样本很大概率由远离的点建模.

from sklearn import datasets
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt

# Loading dataset
iris_df = datasets.load_iris()

# Defining Model
model = TSNE(learning_rate=100)

# Fitting Model
transformed = model.fit_transform(iris_df.data)

# Plotting 2d t-Sne
x_axis = transformed[:, 0]
y_axis = transformed[:, 1]

plt.scatter(x_axis, y_axis, c=iris_df.target)
plt.show()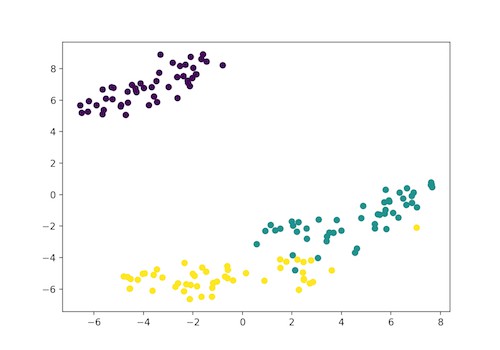

image

图. 紫色: Setosa； 绿色: Versicolor；黄色: Virginica

Iris 数据集包含 4 个特征，即 4d 的，通过 t-SNE 被变换为二维图像表示. 类似地，t-SNE 也可以用到 n 维特征的数据集.

3.5. DBSCAN 聚类

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)，即，具有噪声的基于密度的聚类方法，其是一种流行的聚类算法，用于预测分析中代替 KMeans. 它不要求初始化聚类数目，即可运行. 但必须调整其它两个参数.

scikit-learn 库实现提供了 eps 和 min_samples 参数的默认值，但这些参数往往需要调整. eps 参数是在同一邻域中考虑的两个数据点之间的最大距离. min_samples 参数是被认为是聚类的邻域中的数据点的最小量.

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.decomposition import PCA

# Load Dataset
iris = load_iris()

# Declaring Model
dbscan = DBSCAN()

# Fitting
dbscan.fit(iris.data)

# Transoring Using PCA
pca = PCA(n_components=2).fit(iris.data)
pca_2d = pca.transform(iris.data)

# Plot based on Class
for i in range(0, pca_2d.shape[0]):
    if dbscan.labels_[i] == 0:
        c1 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c='r', marker='+')
    elif dbscan.labels_[i] == 1:
        c2 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c='g', marker='o')
    elif dbscan.labels_[i] == -1:
        c3 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c='b', marker='*')

plt.legend([c1, c2, c3], ['Cluster 1', 'Cluster 2', 'Noise'])
plt.title('DBSCAN finds 2 clusters and Noise')
plt.show()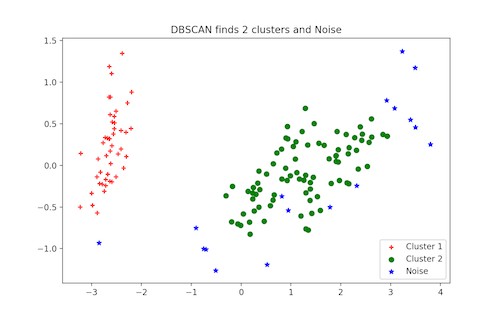

image

4. 更多无监督技术

  • Principal Component Analysis (PCA)
  • Anomaly detection
  • Autoencoders
  • Deep Belief Nets
  • Hebbian Learning
  • Generative Adversarial Networks(GANs)
  • Self-Organizing maps

5. 相关链接

[1] - Supervised Learning In Python

[2] - Introduction To Machine Learning

[3] - Deep Learning with Python

[4] - Linear Algebra for Deep Learning

Last modification：January 23rd, 2019 at 02:25 pm
© 允许规范转载