原文:Artificial Inteligence - Chapter 3.2 - Convolutional Neural Networks
CNN 由多个网络层组成,利用卷积核学习输入数据的有用信息. 卷积核的参数通过"学习"来进行自动调整,以提取任务场景所需的最有用的信息,而不用手工提取特征. CNN 更适用于图像应用.
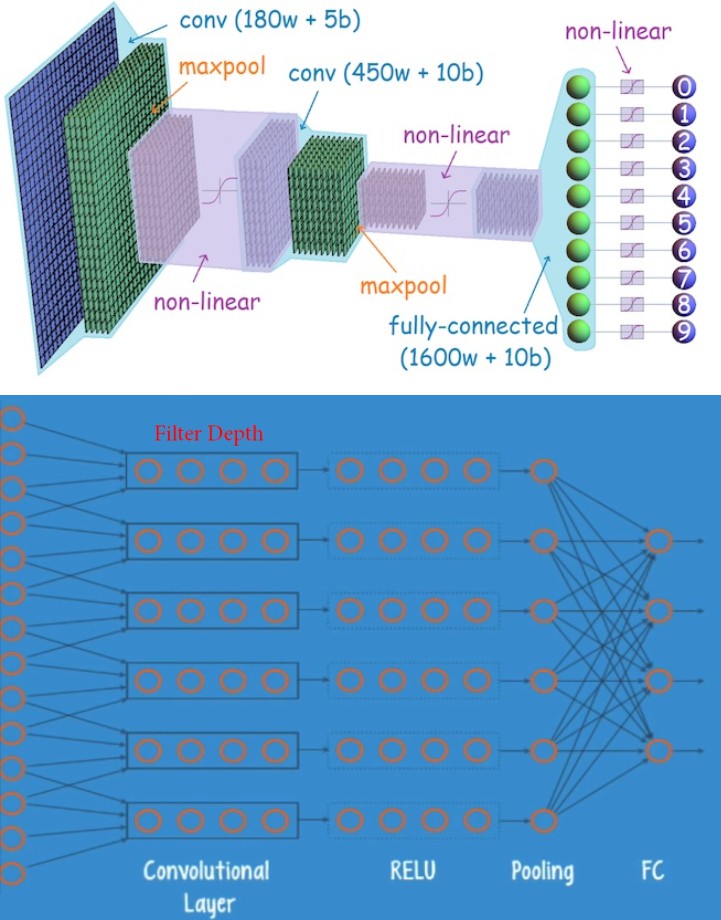
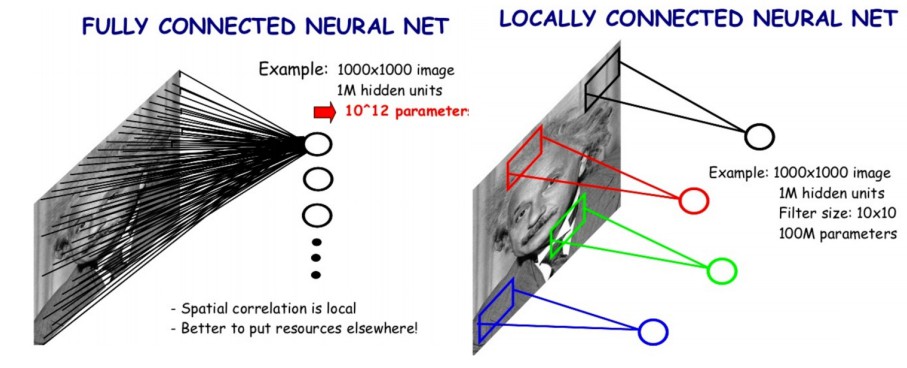
1. 与全连接神经网络的对比
全连接神经网络,需要先将图像转换为一个一维向量 - 1d vector [1, (width.height.channels)],然后将向量数据送入一个全连接的隐藏层.
如图(左):1000x1000 的图片,输入到 1M 个隐藏神经元,采用全连接层,该隐藏层会有 $10^{12}$ 个参数.
如图(右):1000x1000 的图片,输入到 1M 个隐藏神经元,采用卷积核,该隐藏层只有 100M 个参数.
2. CNN 通用结构
一般模式是,CONV->ReLU->Pool->CONV->ReLU->Pool->FC->Softmax_loss. (如 VGGNet).

3. CNN 关键部件 - Conv 层
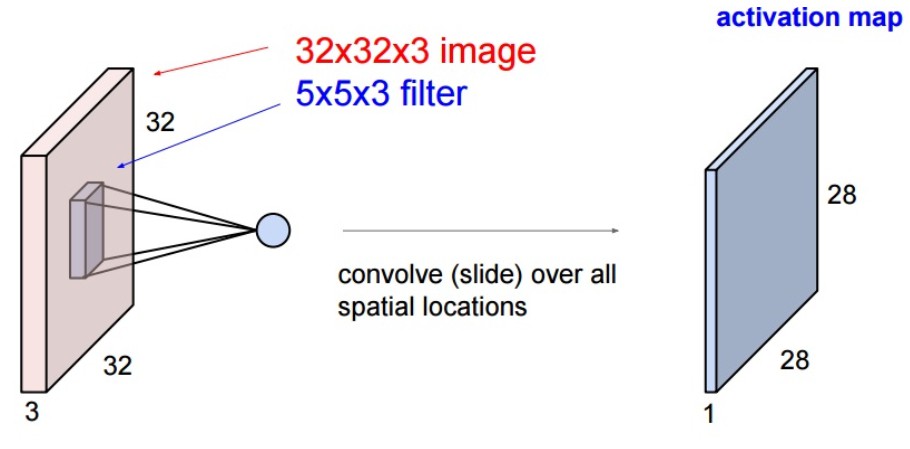
CNN 中最重要的操作是卷积层,对输入进行卷积操作.
对于 32x32x3 的图像,采用 5x5x3 的卷积操作(卷积核深度必须与输入图像的深度一致),则输出结果的特征图维度为 28x28x1(stride=1).

卷积核的作用相当于对图像进行特征提取,每个卷积核提取整张图像的某个特征.
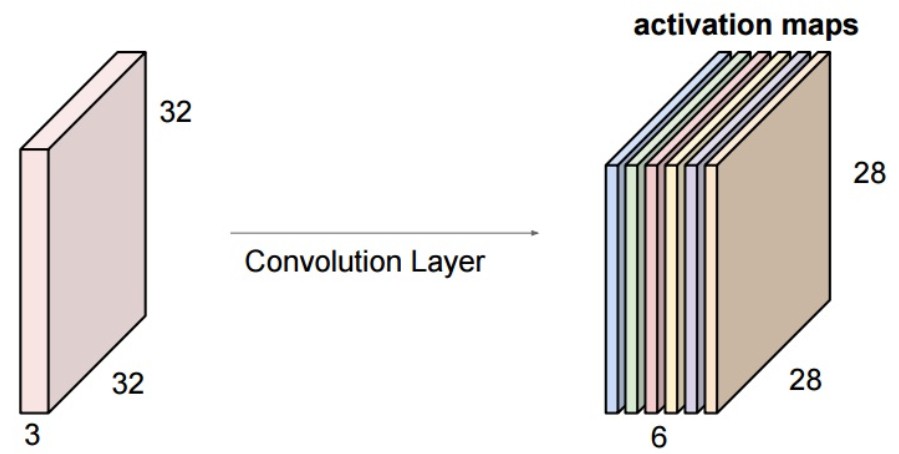
如果需要卷积层提取 6 种不同的特征图,则需要 6 个 5x5x3 卷积核(filters),每一个卷积核分别对图片进行特征提取操作.
卷积操作其自身是一种线性操作,如果要避免线性分类器的问题,则需要在卷积层后添加一个非线性层(如,常用的 ReLU 层).
采用卷积进行模式匹配另一个重要因素是,图片中待搜索特征与位置的不相关性. 神经网络在训练过程中,会对目标所在位置进行精确特征提取.

4. 卷积层超参数
卷积层涉及的参数有:
[1] - KernelSize(K) - 越小越好(但,如果在第一层,会消耗较多内存).
[2] - Stride(S) - 步长,conv 层一般为 1,pooling 层一般为 2.
[3] - ZeroPadding(pad) - 图像边界补零数,以使 conv 层的输出尺寸能够与输入尺寸相同(F=1, PAD=0; F=3, PAD=1; F=5, PAD=2; F=7, PAD=3).
[4] - Number of Filters(F) - conv 层提取的特征数.
4.1 卷积层输出尺寸
默认情况下,conv 层输出一般比输入的尺寸小. 对此,需要采用 padding.
conv 层输出尺寸的计算公式如下:
$H_{out} = 1 + \frac{H_{in} + (2 \cdot pad) - K_{height}}{S} $
$W_{out} = 1 + \frac{W_{in} + (2 \cdot pad) - K_{width}}{S} $
4.2 卷积操作可视化
conv_arithmetic
对于 4x4 的输入,采用 filter 3x3 (K=3), stride (S=1), padding (pad=0) 的卷积操作:
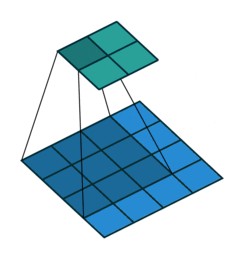
对于 5x5 的输入,采用 filter 3x3 (k=3), stride (S=1), padding (pad=1) 的卷积操作:

4.3 参数量(权重)
卷积层的参数量计算.
$num_{parameters} = ((F * F * depth_{input}) + 1) * num_{filters}$
Input:32x32x3 RGB 图像
Conv:Kernel(F):5x5, Stride:1, Pad:2, numFilters:10
参数量:
$num_{parameters} = ((5 * 5 * 3) + 1) * 10 = 760$
其中 +1 是 bias 项(可以忽略,简化计算).
4.4 内存占用量
卷积层所占用的内存量计算.
Input:32x32x3 RGB 图像
Conv:Kernel(F):5x5, Stride:1, Pad:2, numFilters:10
采用了 pad,故 conv 层的输出为 32x32x10,因此,内存占用量为:10240 bytes.
内存占用量是输出的 4d 张量的维度乘积:
$men = [N_{batch} * C_{depth} * H_{out} * W_{out}]$
4.5 1X1 卷积
1x1 卷积通常用于升维或降维等特征深度处理,合并 1x1 卷积的时候,不会修改其空间信息.
5. 取代大卷积核
这里介绍连续几个小卷积核的作用,如下图中有 2 个 3x3 conv 层. 从右边的 Second 层开始往左,其有 3x3 接受野,且在 First 层的每个神经元对于输入有 5x5 接受野.
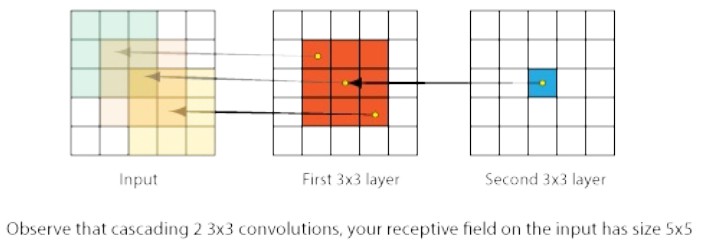
故,简而言之,连续的小卷积核可以用于表示更大的卷积核.
很多优秀的模型开始趋向于采用较小的卷积核. 例如,一个 7x7 卷积核,可以取代为相同深度的 3 个 3x3 卷积核. 但不能用于第一个 Conv 层,因为,第一个 conv 层和输入的 input 的 depth 间不匹配(除非第一层只有 3 个卷积核.)
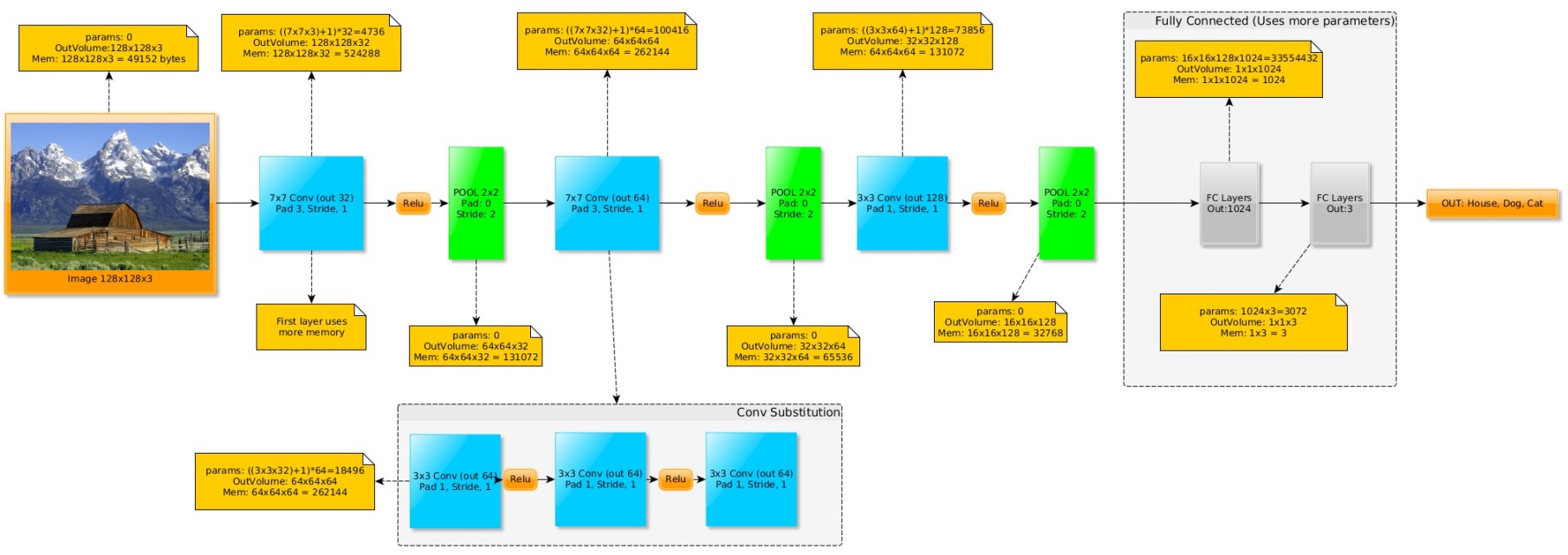
如图,将 7x7 卷积替换为 3 个 3x3 卷积,因为每个卷积层后均有 ReLU 层,因此具有更好的非线性. 此外,权重和 multiply-add 操作更少,计算速度更快.
5.1 计算 7x7 卷积的替换
假设 C 个卷积核的 7x7 卷积,应用于 WxHxC 的输入数据,则,权重量计算为:
$num\_Weights\_7x7 = C(7×7×C) = 49 C^2$
如果采用 3 个 C 个卷积核的 3x3 卷积,则权重量计算为:
$3 × num\_Weights\_3x3 = 3×C(3×3×C) = 27 C^2$
因为采用了在卷积层间更多的 ReLU 操作,非线性更强,参数量更少,性能更优.
5.2 取代第一个卷积层
正如前面所说,不能取代第一个卷积层. 实际上第一个卷积层采用小卷积核,会造成更多的内存消耗.
对于 64 个卷积核步长为 1 的 3x3 卷积,其与步长为 2 的 7x7 卷积具有相同的深度(depth):
$mem_{3x3} = 256×256×64 = 4Mb$
5.3 采用Bottleneck 进行 3x3 卷积核替换
一种能够采用 3x3 卷积的机制是 bottleneck 层. 其与正常的 3x3 卷积表示形式相同,但参数更少,非线性更强.
如图, 3x3 卷积核的取代,与前一层具有相同的深度(图中是 50x50x64).

Bottleneck 的参数量计算:
$((1×1×C)×C/2) + (3×3×C/2 × C/2) + ((1×1×C/2)×C) = 3.25 C^2$
而 3x3 卷积核的参数为 $9 C^2$.
Bottleneck 也被用于 Residual 网络:
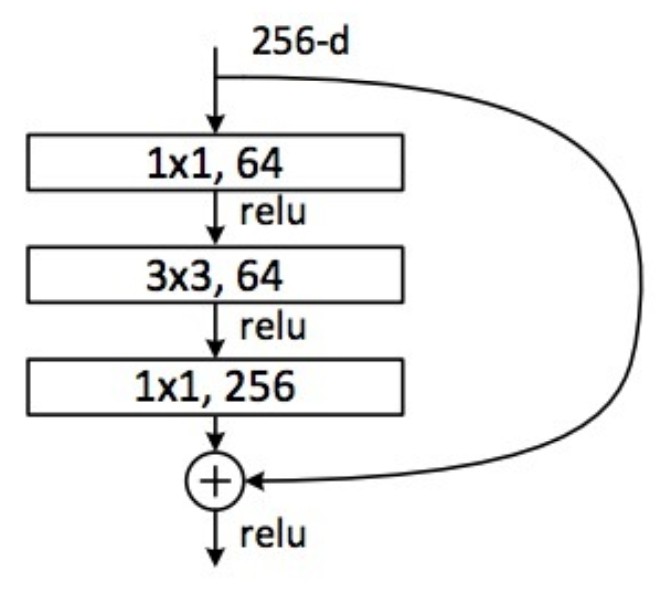
另一种分解 3x3xC 卷积的方式是,采用 1x3xC + 3x1xC. 其被应用于 residual Inception 层中.
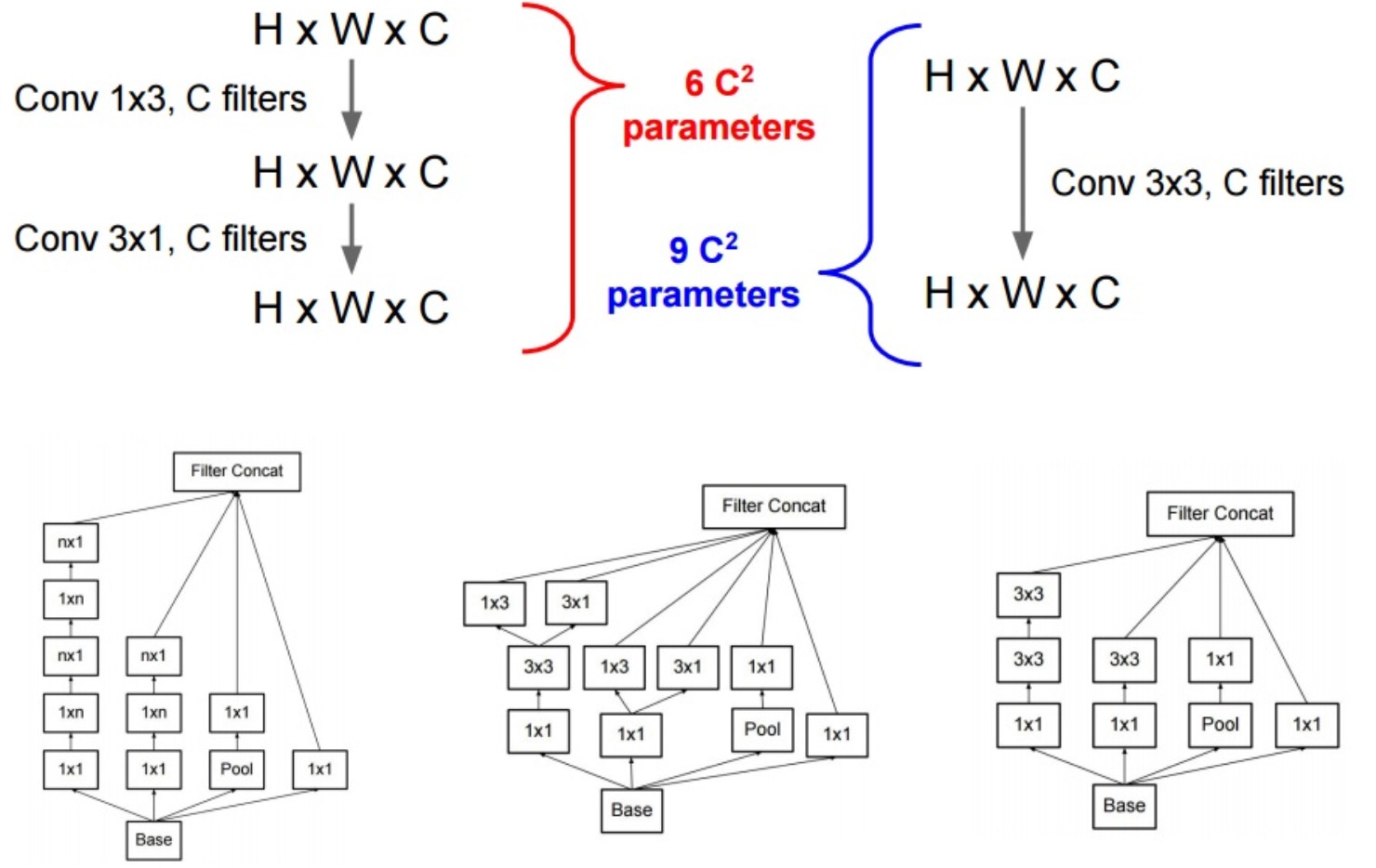
6. FC 层到 Conv 层的转换
网络结构中可以将全连接层 FC 层转换为 Conv 层,反之亦然. 但这里更关注于 FC 转换为 Conv 层,以提升网络性能.
例如,输出为 K=4096 的 FC层和 7x7x512 的输入,起转换为Conv 层为:
CONV: Kernel:7x7, Pad:0, Stride:1, numFilters:4096
采用 2D 卷积:
$output\_Size_W = 1 + \frac{W - F + 2P}{S} = 1 + \frac{7 - 7 + 2×0}{1}$
则输出为 1x1x4096.
FC 层转换为 Conv 层的好处有:
[1] - 性能更好 - 由于 Conv 的权重共享,计算更快.
[2] - 更大尺寸的图片输入
[3] - 可以同时检测相同图片的两个目标物体(如果采用了更大尺寸的图像),最终的输出也比单个列向量更大.

7. 感受野计算
Calculating Receptive Field of CNN
感受野是卷积的一个特定窗口,其表示自己所能"看到"的输入张量.
第 $k$ 层的接受野 $l_k$ 的计算:
$l_k = l_{k-1} + ((f_k - 1) * \prod _{i=1}^{k-1} s_i)$
其中,$l_{k-1}$ 为第 $k-1$ 层的接受野,$f_k$ 是卷积核尺寸(height 或 width,这里假设 height=width),$s_i$ 是第 $i$ 层的步长(stride).
该公式计算了网络结构从下往上的接受野(从网络第一层开始).
直观的,第 $k$ 层的接受野,相比于第 $k-1$ 层,多覆盖了 $(f_k - 1) * s_{k-1}$ 个像素. 然而,该增量需要转换到第一层,故该增量是阶乘的(factorial) - 在第 $k-1$ 层的步长比在更低网络层是指数级的.
