原文:Diffusion Model Clearly Explained! - 2022.12.26
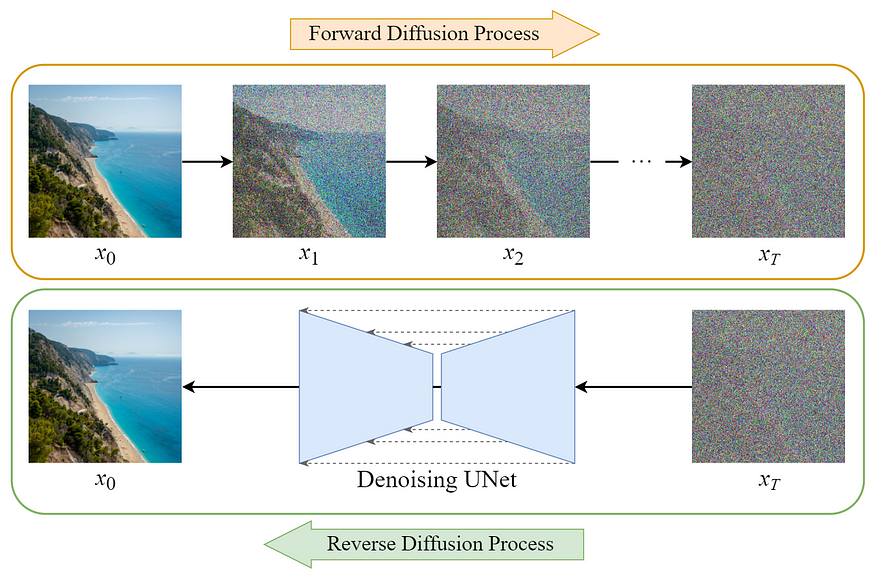
图:Diffusion Model 概览
Diffusion Model 的训练可以分为两部分:
[1] - Forward Diffusion Process -> add noise to the image
[2] - Reverse Diffusion Process -> remove noise from the image
Forward Diffusion Process

图:Forward diffusion process
Forward diffusion process 是逐渐 step-by-step 的向输入图像 $x_0$ 添加 Gaussion noise,共有 $T$ steps. 过程中会得到噪声图像序列 $x_1, x_2, ..., x_T$.
当 $T \rightarrow \infin $ 时,最终的结果就会完全变成噪声图像,只要噪声是从各项同性(isotropic) Gaussian distribution 中采样的.
但是,相比于设计迭代添加噪声到图像的算法,可以采用 closed-form formula 来直接在特定 timestep $t$ 采样噪声图像.
Closed-Form formula
closed-form sampling formula 可以采用 Reparameterization Trick 推导得到,
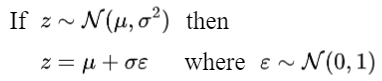
图:Reparameterization trick
基于该表达式,可以将采样图像 $x_t$ 表示为:
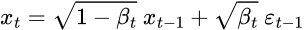
然后,递归展开,得到 closed-form formula:
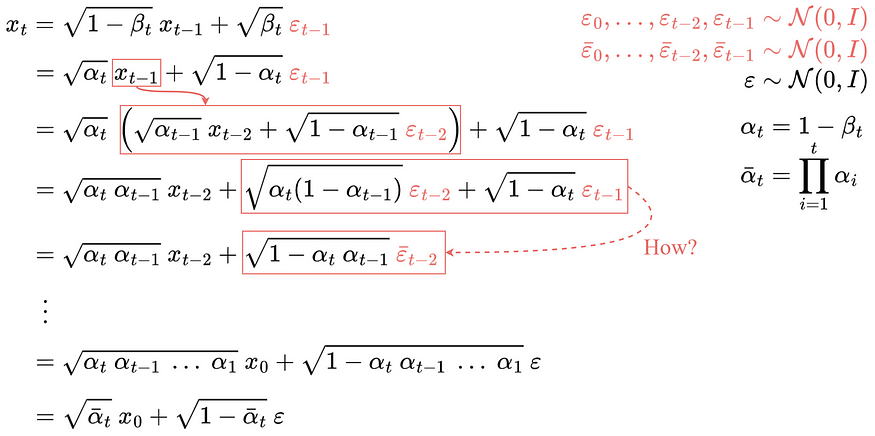
注:
所有的 $\varepsilon$ 都是 i.i.d,标准正态分布
但是,如何从第 4 行得到的第 5 行呢?
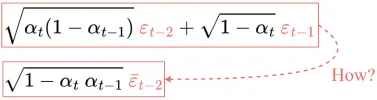
其推导过程,如:

最终,即可得到只依赖于输入图像 $x_0$ 的公式.
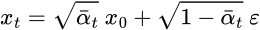
因此,即可采用该公式在任意 timestep 直接采样 $x_t$,其使得 forward process 快了很多.
Reverse Diffusion Process
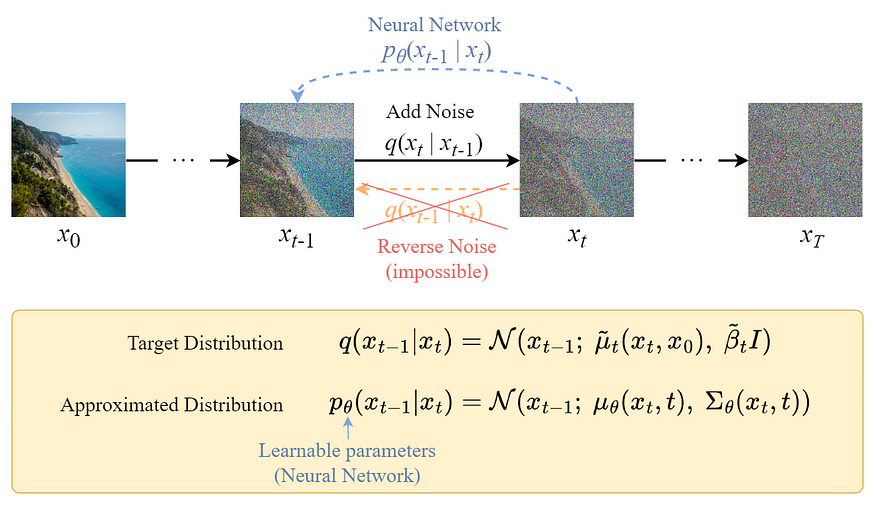
图: Reverse diffusion process
与 Forward Process 不同,不能直接采用 $q_{t-1} | x_t$ 逆向得到噪声,因为比较难以计算.
因此,需要训练一个神经网络 $p \theta (x_{t-1} | x_t)$ 来逼近 $q(x_{t-1} | x_t)$.
逼近形式 $p \theta (x_{t-1} | x_t)$ 遵循正态分布,其均值和方差,
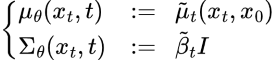
Loss Function
损失函数定义为 Negative Log-Likelihood:
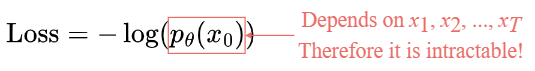
类似于 VAE,相比于优化损失函数本身,可以优化其Variational Lower Bound.
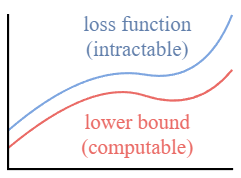
通过优化 computable lower bound,即可间接优化目标损失函数.

根据展开的 variational lower bound 公式,可以看出,其主要包含三项:
[1] - $L_T$,常数项
因为 $q$ 没有可学习参数,$p$ 只是 Gaussian noise probability,因此,该项训练时是常数项,可以忽略.
[2] - $L_{t-1}$,stepwise denosing 项
该项对比 target denoising step $q$ 和逼近的 denoising step $p_{\theta}$.
注:通过对 $x_0$ 添加条件,$q(x_{t-1} | x_t, x_0)$ 的计算变得容易.

图:Details of the stepwise denoising term
为了逼近 target denoising step $q$,只需要采用神经网络逼近其均值. 因此,设置逼近的均值 $\mu _{\theta}$ 与 target 均值 $\hat {\mu_{t}}$ 具有相同的形式.
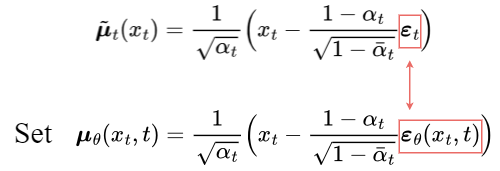
target 均值和逼近均值的比较,采用 MSE 计算,

经验地,忽略权重项,仅对比 target 和 predicted noises 的 MSE,能够活的更好的结果.
因此可以看出,逼近期望的 denoising step $q$,只需要采用神经网络 $\varepsilon _{\theta}$ 逼近 noise $\varepsilon _{t}$.
[3] - $L_0$,Reconstruction term
last denosing step 的重建损失,因此训练时可以忽略,因为,
- 其可以采用 $L_{t-1}$ 相同的神经网络进行逼近.
- 忽略该项,可以使得采样质量更好,且更易于实现.
简化后损失
简化后的损失函数,如
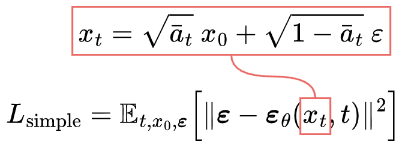
U-Net
Dataset
每个 epoch 中,
[1] - 对于每个训练样本(图像),随机选择 timestep $t$
[2] - 将对应于 $t$ 的 Gaussian noise,应用到每张图像
[3] - 将 timestep 转换为 embeddings(vectors)
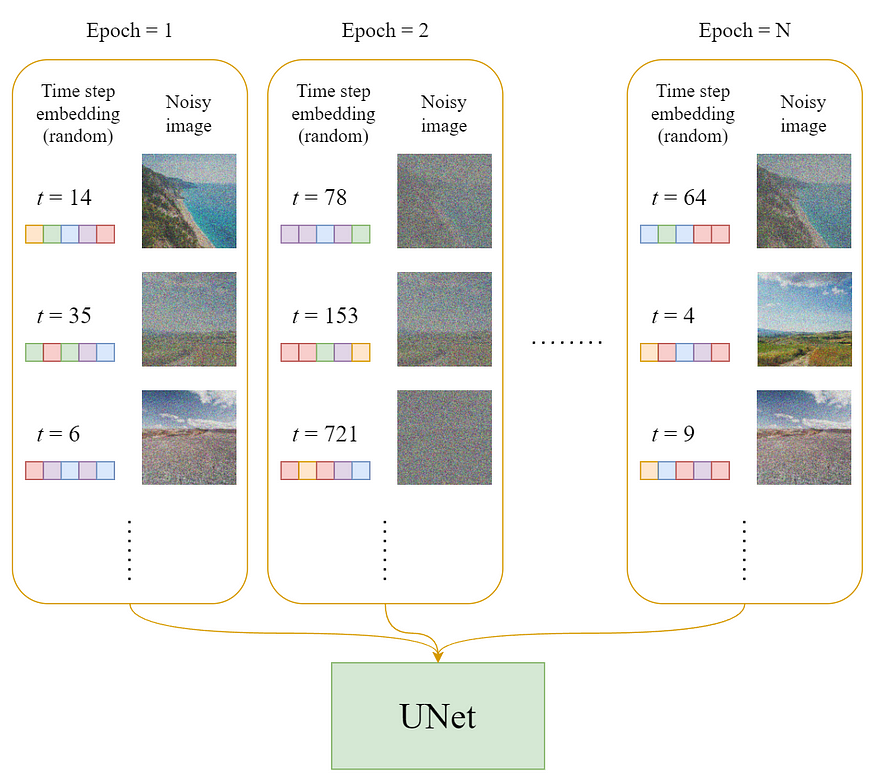
Training
训练流程如,

一个 training step 的流程例示,
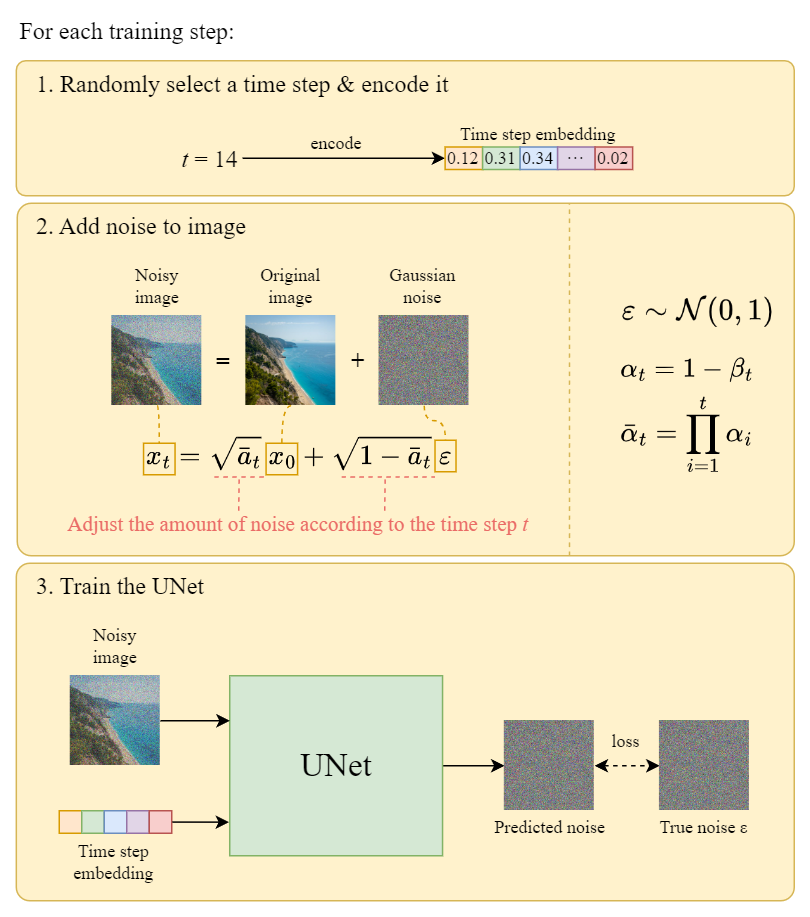
图:Training step illustration
Reverse Diffusion

基于以上算法,可以从 noises 中生成图像. 如下是例示,
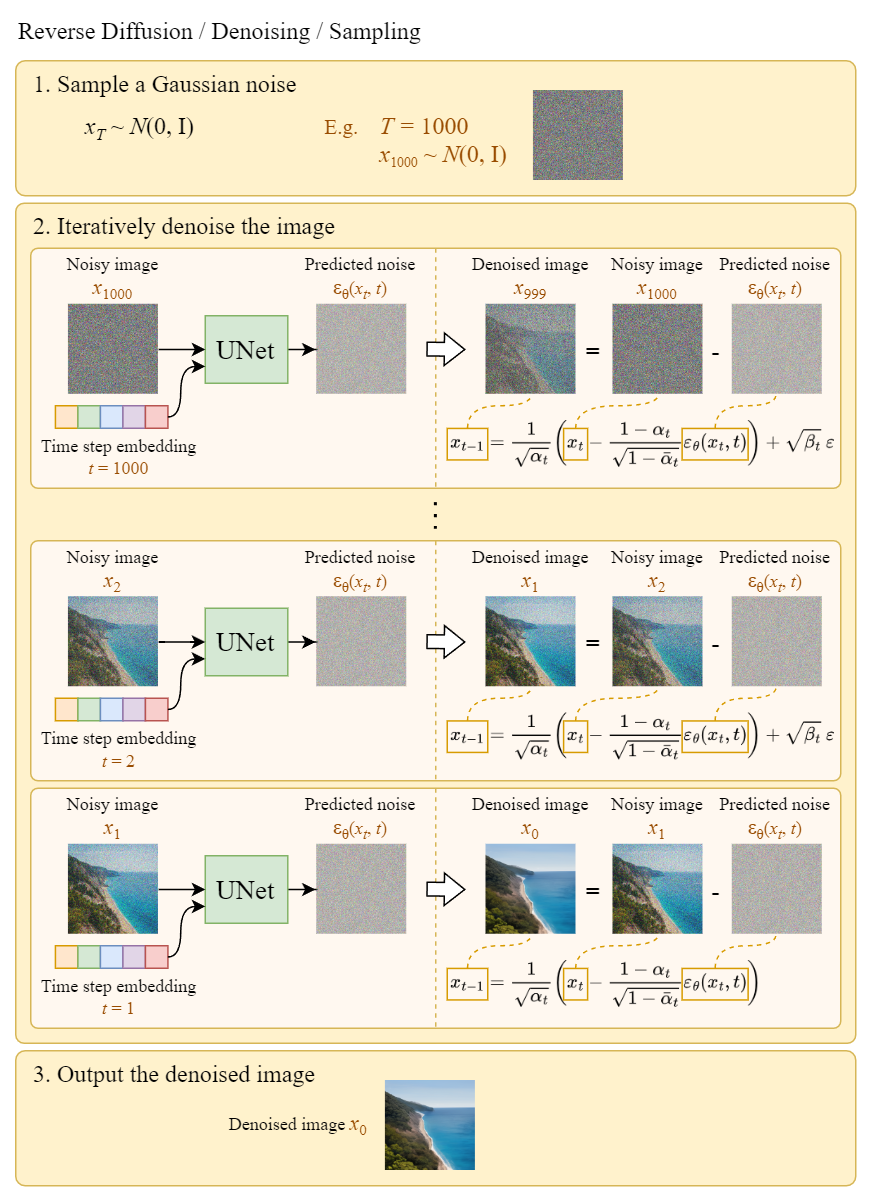
图:Sampling illustration
注意,在 last step 中,只是简单的输出学习的均值 $\mu _{\theta} (x_1, 1) $,并没有对其添加噪声.
Summary
- Diffusion model 可以分为两部分, forward diffusion 和 reverse diffusion.
- forward diffusion 可以采用 closed-form formula 来实现
- backward diffusion 可以采用训练神经网络来实现
- 为了逼近期望的 denoising step $q$,只需采用神经网络 $\varepsilon _{\theta}$ 逼近 noise $\varepsilon _{t}$
- 在简化损失函数上的训练可以得到更好的采样质量
References
[1] K. Roose, “An a.i.-generated picture won an art prize. artists aren’t happy.,” The New York Times, 02-Sep-2022. [Online]. Available: https://www.nytimes.com/2022/09/02/technology/ai-artificial-intelligence-artists.html.
[2] J. Ho, A. Jain, and P. Abbeel, “Denoising Diffusion Probabilistic models,” arXiv.org, 16-Dec-2020. [Online]. Available: https://arxiv.org/abs/2006.11239.
[3] N. A. Sergios Karagiannakos, “How diffusion models work: The math from scratch,” AI Summer, 29-Sep-2022. [Online]. Available: https://theaisummer.com/diffusion-models.
[4] L. Weng, “What are diffusion models?,” Lil’Log, 11-Jul-2021. [Online]. Available: https://lilianweng.github.io/posts/2021-07-11-diffusion-models/.
[5] A. Seff, “What are diffusion models?,” YouTube, 20-Apr-2022. [Online]. Available: https://www.youtube.com/watch?v=fbLgFrlTnGU.
[6] Outlier, “Diffusion models | paper explanation | math explained,” YouTube, 06-Jun-2022. [Online]. Available: https://www.youtube.com/watch?v=HoKDTa5jHvg.