出处:Paddle文档平台 - 池化
1. 基础概念
在图像处理中,由于图像中存在较多冗余信息,可用某一区域子块的统计信息(如最大值或均值等)来刻画该区域中所有像素点呈现的空间分布模式,以替代区域子块中所有像素点取值,这就是卷积神经网络中池化(pooling)操作。
池化操作对卷积结果特征图进行约减,实现了下采样,同时保留了特征图中主要信息。比如:当识别一张图像是否是人脸时,我们需要知道人脸左边有一只眼睛,右边也有一只眼睛,而不需要知道眼睛的精确位置,这时候通过池化某一片区域的像素点来得到总体统计特征会显得很有用。
池化的几种常见方法包括:平均池化、最大池化、K-max池化。其中平均池化和最大池化如 图1 所示,K-max池化如 图2 所示。
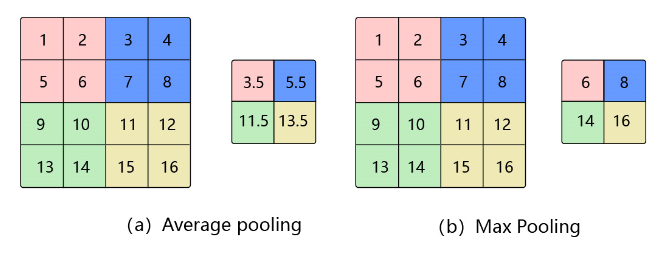
图1 平均池化和最大池化
1.1. 平均池化
计算区域子块所包含所有像素点的均值,将均值作为平均池化结果。如 图1(a),这里使用大小为$2\times2$的池化窗口,每次移动的步幅为2,对池化窗口覆盖区域内的像素取平均值,得到相应的输出特征图的像素值。池化窗口的大小也称为池化大小,用$k_h \times k_w$表示。在卷积神经网络中用的比较多的是窗口大小为$2 \times 2$,步幅为2的池化。
1.2. 最大池化
从输入特征图的某个区域子块中选择值最大的像素点作为最大池化结果。如 图1(b),对池化窗口覆盖区域内的像素取最大值,得到输出特征图的像素值。当池化窗口在图片上滑动时,会得到整张输出特征图。
1.3. K-max池化
对输入特征图的区域子块中像素点取前K个最大值,常用于自然语言处理中的文本特征提取。如图2,从包含了4个取值的每一列中选取前2个最大值就得到了K最大池化结果。
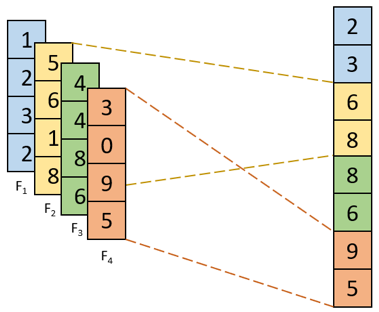
图2 K-max池化
2. 特点
[1] - 当输入数据做出少量平移时,经过池化后的大多数输出还能保持不变,因此,池化对微小的位置变化具有鲁棒性。例如 图3 中,输入矩阵向右平移一个像素值,使用最大池化后,结果与平移前依旧能保持不变。
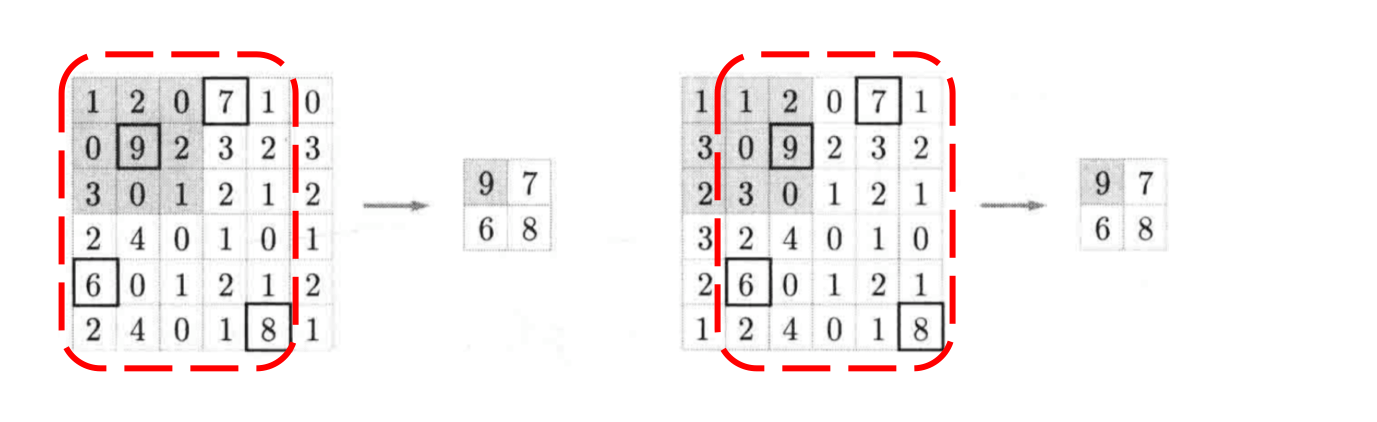
图3 微小位置变化时的最大池化结果
[2] - 由于池化之后特征图会变小,如果后面连接的是全连接层,能有效的减小神经元的个数,节省存储空间并提高计算效率。
3. 应用示例
与卷积核类似,池化窗口在图片上滑动时,每次移动的步长称为步幅,当宽和高方向的移动大小不一样时,分别用$s_w$和$s_h$表示。也可以对需要进行池化的图片进行填充,填充方式与卷积类似,假设在第一行之前填充$p_{h1}$行,在最后一行后面填充$p_{h2}$行。在第一列之前填充$p_{w1}$列,在最后一列之后填充$p_{w2}$列,则池化层的输出特征图大小为:
$$H_{out} = \frac{H + p_{h1} + p_{h2} - k_h}{s_h} + 1$$
$$W_{out} = \frac{W + p_{w1} + p_{w2} - k_w}{s_w} + 1$$
在卷积神经网络中,通常使用$2\times2$大小的池化窗口,步幅也使用2,填充为0,则输出特征图的尺寸为:
$$H_{out} = \frac{H}{2}$$
$$W_{out} = \frac{W}{2}$$
通过这种方式的池化,输出特征图的高和宽都减半,但通道数不会改变。
这里以 图1 中的2个池化运算为例,此时,输入大小是$4 \times 4$ ,使用大小为$2 \times 2$ 的池化窗口进行运算,步幅为2。此时,输出尺寸的计算方式为:
$$H_{out} = \frac{H + p_{h1} + p_{h2} - k_h}{s_h} + 1=\frac{4 + 0 + 0 - 2}{2} + 1=\frac{4}{2}=2$$
$$W_{out} = \frac{W + p_{w1} + p_{w2} - k_w}{s_w} + 1=\frac{4 + 0 + 0 - 2}{2} + 1=\frac{4}{2}=2$$
图1(a) 中,使用平均池化进行运算,则输出中的每一个像素均为池化窗口对应的 $2 \times 2$ 区域求均值得到。计算步骤如下:
[1] - 池化窗口的初始位置为左上角,对应粉色区域,此时输出为 $3.5 = \frac{1 + 2 + 5 + 6}{4}$ ;
[2] - 由于步幅为2,所以池化窗口向右移动两个像素,对应蓝色区域,此时输出为 $5.5 = \frac{3 + 4 + 7 + 8}{4}$ ;
[3] - 遍历完第一行后,再从第三行开始遍历,对应绿色区域,此时输出为 $11.5 = \frac{9 + 10 + 13 + 14}{4}$ ;
[4] - 池化窗口向右移动两个像素,对应黄色区域,此时输出为 $13.5 = \frac{11 + 12 + 15 + 16}{4}$ 。
图1(b) 中,使用最大池化进行运算,将上述过程的求均值改为求最大值即为最终结果。
4. 反向梯度计算
参考:深度学习笔记(3)——CNN中一些特殊环节的反向传播
CNN网络中另外一个不可导的环节就是Pooling池化操作,因为Pooling操作使得feature map的尺寸变化,假如做2×2的池化,假设那么第l+1层的feature map有16个梯度,那么第l层就会有64个梯度,这使得梯度无法对位的进行传播下去。其实解决这个问题的思想也很简单,就是把1个像素的梯度传递给4个像素,但是需要保证传递的loss(或者梯度)总和不变。根据这条原则,mean pooling和max pooling的反向传播也是不同的。
4.1. 平均池化
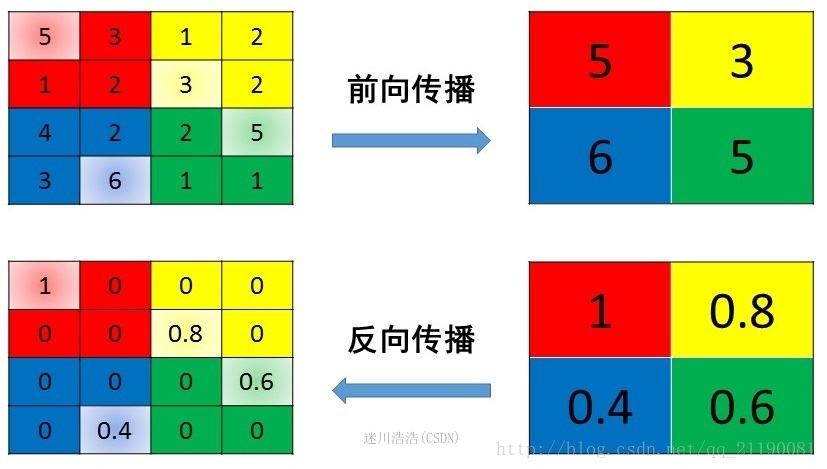
MeanPooling的前向传播就是把一个patch中的值求取平均来做pooling,那么反向传播的过程也就是把某个元素的梯度等分为n份分配给前一层,这样就保证池化前后的梯度(残差)之和保持不变,图示如:
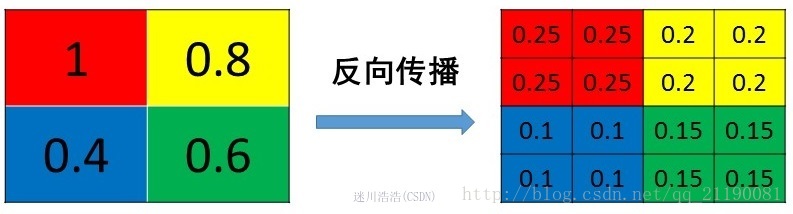
MeanPooling比较容易让人理解错的地方就是会简单的认为直接把梯度复制N遍之后直接反向传播回去,但是这样会造成loss之和变为原来的N倍,网络是会产生梯度爆炸的。
4.2. 最大池化
MaxPooling也要满足梯度之和不变的原则,MaxPooling 的前向传播是把patch中最大的值传递给后一层,而其他像素的值直接被舍弃掉。那么反向传播也就是把梯度直接传给前一层某一个像素,而其他像素不接受梯度,也就是为0。所以MaxPooling操作和MeanPooling操作不同点在于需要记录下池化操作时到底哪个像素的值是最大,也就是max id,这个变量就是记录最大值所在位置的,因为在反向传播中要用到,那么假设前向传播和反向传播的过程就如下图所示 :