出处:Paddle文档平台 - 基础知识
1. 神经元
在生物学中,神经元细胞有兴奋与抑制两种状态。大多数神经元细胞在正常情况下处于抑制状态,一旦某个神经元受到刺激并且电位超过一定的阈值后,这个神经元细胞就被激活,处于兴奋状态,并向其他神经元传递信息。基于神经元细胞的结构特性与传递信息方式,神经科学家 Warren McCulloch 和逻辑学家 Walter Pitts 合作提出了“McCulloch–Pitts (MCP) neuron”模型。在人工神经网络中,MCP模型成为人工神经网络中的最基本结构。MCP模型结构如 图1 所示。
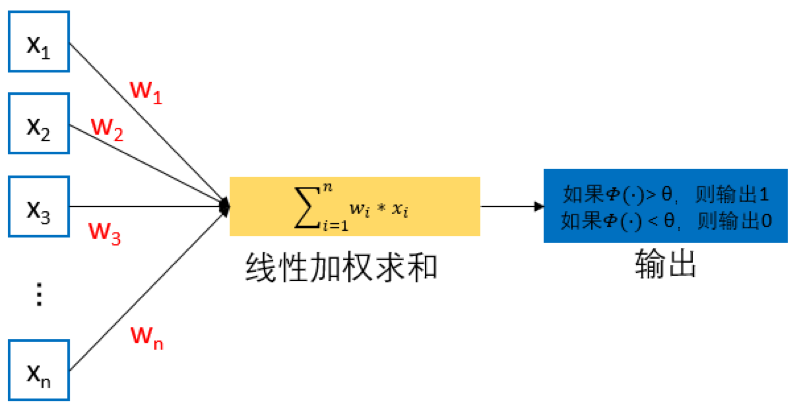
图1 MCP 模型结构
从 图1 可见,给定 n 个二值化(0或1)的输入数据 $x_i$ ($1\le i\le n$)与连接参数 $w_i$ ($1\le i\le n$),MCP 神经元模型对输入数据线性加权求和,然后使用函数 $\varPhi \left( \right)$ 将加权累加结果映射为 0 或 1 ,以完成两类分类的任务:
$$ y=\varPhi \left( \sum_{i=1}^n{w_ix_i} \right) $$
其中 $w_i$ 为预先设定的连接权重值(一般在 0 和 1 中取一个值或者 1 和 -1 中取一个值),用来表示其所对应输入数据对输出结果的影响(即权重)。$\varPhi \left( \right)$ 将输入端数据与连接权重所得线性加权累加结果与预先设定阈值 $\theta$ 进行比较,根据比较结果输出 1 或 0。
具体而言,如果线性加权累加结果(即 $\sum_{i=1}^m{w_ix_i}
$)大于阈值 $\theta$,则函数 $\varPhi \left( \right)$ 的输出为1、否则为0。也就是说,如果线性加权累加结果大于阈值 $\theta$,则神经元细胞处于兴奋状态,向后传递 1 的信息,否则该神经元细胞处于抑制状态而不向后传递信息。
从另外一个角度来看,对于任何输入数据 $x_i$ ($1\le i\le n$),MCP 模型可得到 1 或 0 这样的输出结果,实现了将输入数据分类到 1 或 0 两个类别中,解决了二分类问题。
2. 单层感知机
2.1. 单层感知机模型
1957年 Frank Rosenblatt 提出了一种简单的人工神经网络,被称之为感知机。早期的感知机结构和 MCP 模型相似,由一个输入层和一个输出层构成,因此也被称为“单层感知机”。感知机的输入层负责接收实数值的输入向量,输出层则为1或-1两个值。单层感知机可作为一种二分类线性分类模型,结构如 图1 所示。
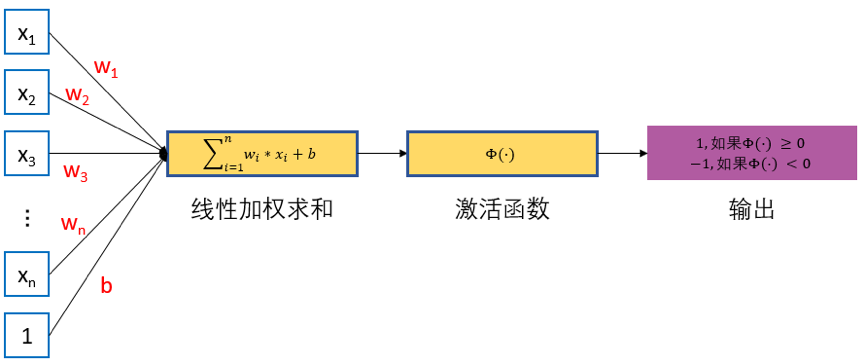
图1 感知机模型
单层感知机的模型可以简单表示为:
$$ f(x) = sign(w*x+b) $$
对于具有 $n$ 个输入 $x_{i}$ 以及对应连接权重系数为 $w_j$ 的感知机,首先通过线性加权得到输入数据的累加结果 $z$:$z=w_1 x_1+w_2 x_2+ ... +b$。这里 $x_1,x_2,...,x_n$ 为感知机的输入,$w_1,w_2,...,w_n$为网络的权重系数,$b$ 为偏置项($bias$)。然后将 $z$ 作为激活函数 $\varPhi(\cdot)$ 的输入,这里激活函数 $\varPhi(\cdot)$为 $sign$ 函数,其表达式为:
$$ sign(x) = \begin{cases} +1 \qquad & x \geq 0 \\ -1 \qquad & x \lt 0 \end{cases} $$
$\varPhi(\cdot)$会将 $z$ 与某一阈值(此例中,阈值为$0$)进行比较,如果大于等于该阈值则感知器输出为 $1$,否则输出为 $-1$。通过这样的操作,输入数据被分类为 $1$ 或 $-1$ 这两个不同类别。
2.2. 训练过程
给定一个 $n$ 维数据集,如果它可以被一个超平面完全分割,那么我们称这个数据集为线性可分数据集,否则,则为线性不可分的数据集。单层感知机只能处理线性可分数据集,其任务是寻找一个线性可分的超平面将所有的正类和负类划分到超平面两侧。单层感知机与 $MCP$ 模型在连接权重设置上是不同的,即感知机中连接权重参数并不是预先设定好的,而是通过多次迭代训练而得到的。单层感知机通过构建损失函数来计算模型预测值与数据真实值间的误差,通过最小化代价函数来优化模型参数。
其具体的训练过程为:
[1] - 定义数据集,变量和参数,其中给定一个$m*n$大小的数据集,$x^0, x^1,...,x^m$ 为训练样本, $x_0^m, x_1^m, ..., x_n^m$为第 $m$ 条训练样本,$d^m$ 为期望结果,$y^m$ 为实际结果,$\eta$ 为学习率,$0 \lt \eta \lt 1$;
[2] - 对权重系数$w_j$进行初始化,初始值为随机值或全零值。同时,设置 $m = 0$,读取第零条训练样本;
[3] - 将训练样本输入到单层感知机中,根据模型公式,得到实际输出 $y$ ;
[4] - 根据如下公式更新权重系数;
$$ w^{m+1} = w^m + \eta[d^m - y^m]x^m $$
[5] - 当满足收敛条件时,算法结束;若不满足收敛条件则输入下一条样本继续训练,即 $m = m +1$。通常收敛条件可为:
- 误差小于某个预先设定的较小值 $\epsilon$ ;
- 迭代的权重系数间权值变化小于某个较小值;
- 迭代次数超过设定的最大迭代次数。
2.3. 单层感知机存在的问题
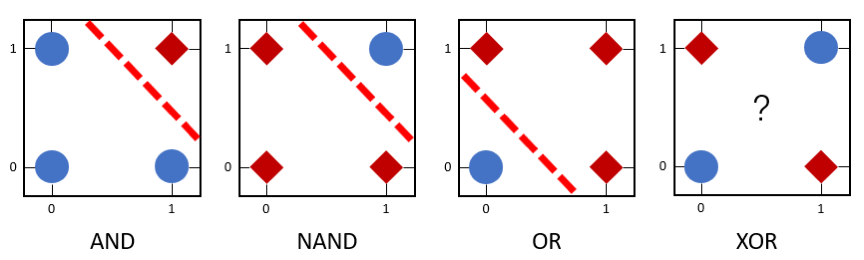
图2 单层感知机模拟不同逻辑函数功能的示意图
单层感知机可被用来区分线性可分数据。在 图2 中,逻辑与(AND)、逻辑与非(NAND)和逻辑或(OR)为线性可分函数,所以可利用单层感知机来模拟这些逻辑函数。但是,由于逻辑异或(XOR)是非线性可分的逻辑函数,因此单层感知机无法模拟逻辑异或函数的功能。
3. 多层感知机
由于无法模拟诸如异或以及其他复杂函数的功能,使得单层感知机的应用较为单一。一个简单的想法是,如果能在感知机模型中增加若干隐藏层,增强神经网络的非线性表达能力,就会让神经网络具有更强拟合能力。因此,由多个隐藏层构成的多层感知机被提出。
如 图1 所示,多层感知机由输入层、输出层和至少一层的隐藏层构成。网络中各个隐藏层中神经元可接收相邻前序隐藏层中所有神经元传递而来的信息,经过加工处理后将信息输出给相邻后续隐藏层中所有神经元。
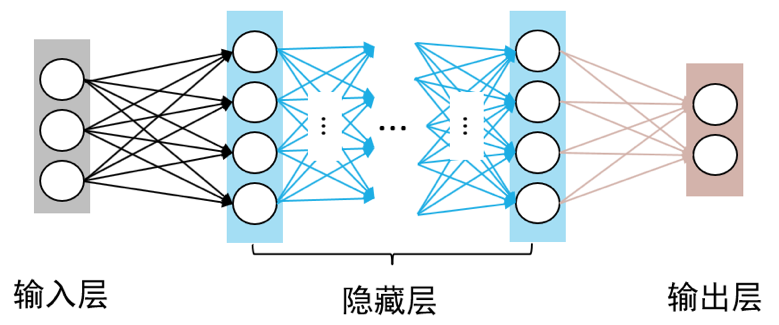
图1 多层感知机模型
在多层感知机中,相邻层所包含的神经元之间通常使用“全连接”方式进行连接。所谓“全连接”是指两个相邻层之间的神经元相互成对连接,但同一层内神经元之间没有连接。多层感知机可以模拟复杂非线性函数功能,所模拟函数的复杂性取决于网络隐藏层数目和各层中神经元数目。