论文理解 - VGGNet - Very Deep Convolutional Networks for Large-Scale Image Recognition[转]

Author： AIHGF
发布时间：May 22, 2018
362views
No comments
43227 words
Categories：图像分类论文阅读

原文 - Very deep convolutional networks for large-scale image recognition
论文: Very Deep Convolutional Networks for Large-Scale Image Recognition
一篇对 VGGNet 理解比较详细的博客，很长很详尽，十分受用.
转载并非常感谢原博主 - Yuens's Blog.

这篇文章是以比赛为目的——解决ImageNet中的1000类图像分类和 localization（这里需要注意 localization 和 detection 的区别. localization是找到某个物体的检测框，而detection是找到所有物体的检测框，后文会详细说明.）

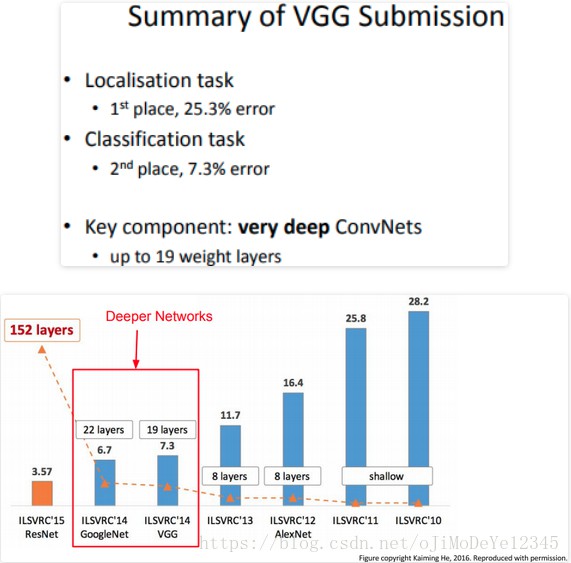
作者对六个网络的实验结果在深度对模型影响方面，进行了感性分析（越深越好），实验结果是16和19层的VGGNet（VGG代表了牛津大学的Oxford Visual Geometry Group，该小组隶属于1985年成立的Robotics Research Group，该Group研究范围包括了机器学习到移动机器人）分类和localization的效果好（作者斩获2014年分类第二，localization第一，分类第一是当年的GoogLeNet.）下面是来自一段对同年的GoogLeNet和VGG的描述：

GoogLeNet和VGG的Classification模型从原理上并没有与传统的CNN模型有太大不同。大家所用的Pipeline也都是：训练时候：各种数据Augmentation（剪裁，不同大小，调亮度，饱和度，对比度，偏色），剪裁送入CNN模型，Softmax，Backprop。测试时候：尽量把测试数据又各种Augmenting（剪裁，不同大小），把测试数据各种Augmenting后在训练的不同模型上的结果再继续Averaging出最后的结果.
参考：如何评价今年的 ILSVRC 2014 结果？ | 知乎
https://www.zhihu.com/question/24904450/answer/29400634

需要注意的是，在VGGNet的6组实验中，后面的几个网络使用了pre-trained model A的某些层来做参数初始化。这点上虽然作者没有提该方法带来的性能增益，但其实是很大的（我会在下文中优秀的特征提取器和泛化能力具体说明.）

上图来自CS231n课程blog的tiny-vggnet模型架构，可以看到有三组卷积后接一个全连接层，每组卷积（blog里称为pattern）的形式都是一样的（conv-relu-conv-relu-pool），实际的VGG16（只算卷积和全连接层的个数是16）与上图略有不同（前两组conv-relu-conv-relu-pool，中间三组conv-relu-conv-relu-conv-relu-pool，最后三个fc，前两个fc是fc-relu-dropout，最后一个fc仅有fc。后文ConvNet
Configurations部分我会具体说明），不过整体来说作者也承认是继承了AlexNet和OverFeat：

继承了AlexNet不少网络结构（基于它加深层数和修改所有卷积核为3×3的小卷积），最后三个fc层基本算是平移AlexNet的到VGGNet上；
继承了OverFeat在Localization任务中的做法（we adopt the approach of Sermanet et al. (2014)，没记错的话OverFeat拿了2013年Localization任务的第一名.）

VGGNet的两个特点：层数更深更宽、卷积核更小. 因为卷积核变小全部改用3×3大小（性能最好的两个网络：实验D（VGG16）和实验E（VGG19）），小卷积核的使用带来参数量减少，可以更加steadily地增加层数得同时不会太过于担心计算量的暴增.因为这篇文章正文写的是分类，附录介绍了VGGNet在localization上的工作，我也会对localization任务的解决进行分析.

这篇文章的主要特别的地方是前两点（换句话说，抄的不是很明显）：

卷积核变小。作者做的6组实验中，卷积核全部替换为3×3（极少用了1×1），选用更小卷积核的motivation是作者受到这两篇文章（Zeiler & Fergus, 2013; Sermanet et al., 2014）启发，使用更小的卷积核尺寸和stride得到性能提升；
层数更深更宽（11层、13层、16层、19层）。我认为作者是觉得：既然小卷积核带来性能提升，那么不妨试试深度对性能的影响，反正参数量我的gpu可以cover住。作者的实验也发现层数越深，带来的分类结果也越好，但并没有提到channel变宽这一个因素：6组实验中channel数都是逐层加宽的，如果单说深度对性能的影响而忽略宽度（这里宽度不是feature map的width而是depth），我觉得并不够convincing，应该再加入一下对宽度（channel）数分析对比的实验；
池化核变小且为偶数。AlexNet中的max-pool全是3×3的，但VGGNet中都是2×2的。作者没有说明选择这种size的考量（现在stride=2、以及2×2和3×3的pooling kernel选择的主流），我认为主要是2×2带来的信息损失相比3×3的比较小，相比3×3更容易捕获细小的特征变化起伏，此外或许是发现2×2的实验效果确实比3×3的好吧（毕竟这也是直接原因）；
网络测试阶段将训练阶段的三个全连接替换为三个卷积。对于训练和测试一样的输入维度下，网络参数量没有变化，计算量也没有变化，思想来自OverFeat，1×1的卷积思想则来自NIN。优点在于全卷积网络可以接收任意尺度的输入（这个任意也是有前提的，长和宽都要满足：$a\times2^n$，n是卷积与池化做stride=2的下采样的次数）；
刷比赛的小技巧。其实没什么意思，比方输入图片的尺寸对于训练和测试阶段的处理方式不同，single和multi-scale的问题（具体见后文）。

下面我将会任务背景开始说明，最后我会再次引用CS231n对于VGG的中肯评价进行总结。

1. 任务背景

因为VGGNet在AlexNet之后，有必要先说一下问题的背景：自从AlexNet将深度学习的方法应用到图像分类取得state of the art的惊人结果后，大家都竞相效仿并在此基础上做了大量尝试和改进，先从两个性能提升的例子说起：

小卷积核。在第一个卷积层用了更小的卷积核和卷积stride（Zeiler & Fergus, 2013; Sermanet et al., 2014）；
多尺度。训练和测试使用整张图的不同尺度（Sermanet et al., 2014; Howard, 2014）。

作者虽然说自己是在保证其他一致，改变深度情况来提升效果的，但实际上也是集大成（抄袭这两个：用更小卷积核；多尺度训练和测试）。算是作者整个实验的motivation吧，既然如此，或许作者想：我再试试深度，如果效果好，就发表出来又水篇文章（毕竟不能没有自己的工作），哈哈哈！

1.1 优秀的特征提取器和泛化能力

1.1.1 特征提取器

另外，作者发现训练出的卷积网络是一个天然的且十分优秀的特征提取器（在不对卷积网络进行fine-tuning而直接在其后接一个SVM分类器并训练该SVM，最终结果也很好），而且特征提取器在其他数据集上具有通用性。说到这点不得不提到RCNN这篇文章，因为该作者将CNN作为一个特征提取器，主要流程是前三个步骤（第四个检测框回归也只是在附录写到，下图是我基于作者修改的图，略有不同）：

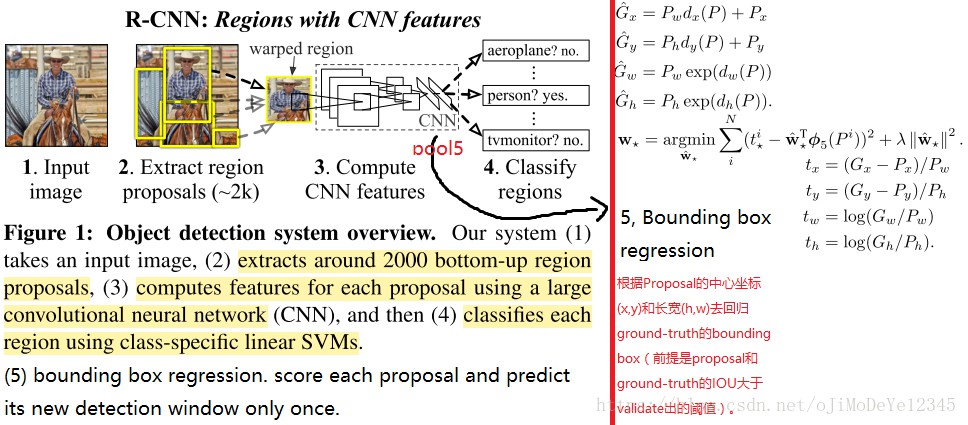
（Supervised pre-training）用12年的分类数据去pre-train模型，CNN后接1k-way softmax
（Domain-specific fine-tuning）用当年20类检测数据集生成分类数据（根据检测数据通过selective search生成小图，然后计算IOU大于0.5视为该类图像），去fine-tune模型，CNN后接20-way softmax；
（Object category classifier）CNN参数固定，训练SVM。输入SVM的数据是CNN处理后的feature map，如果是20类那么对应20个，即分类20类的二分类SVM。其中对于某一类的SVM来说，正样本是proposal和ground-truth的框IOU大于0.3的（交叉验证得到的），其余视为负样本；
（Bounding-box regression）这里原图没有画出，其实在检测这里既有对proposal进行分类，再有对proposal的中心点和宽和高这四个值进行回归的过程，当然这个regressor的参数是训练拿到的。

在此过程中，RCNN作者预训练CNN，之后又用任务数据去fine-tune网络，最后把CNN作为特征提取器给SVM。同样展示了CNN的强大特征提取能力。说到这里不得不提pre-train和fine-tune。

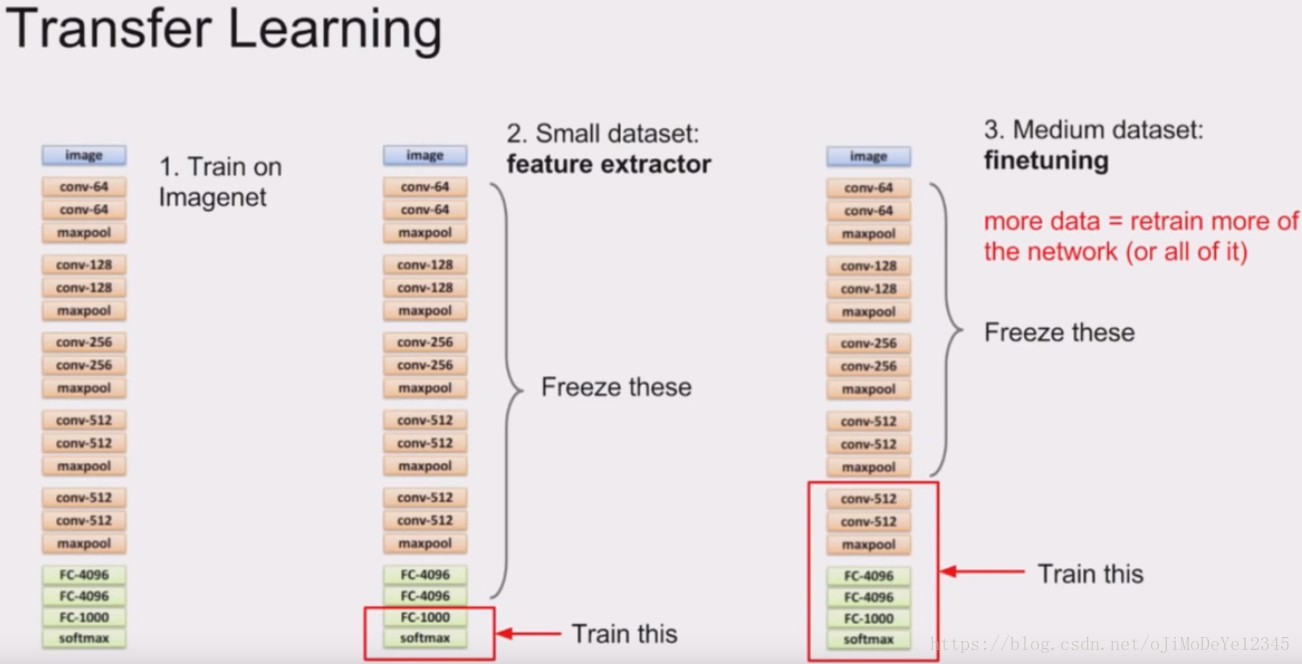
VGGNet 6组实验中的后面几组中用到了pre-train后的A模型的部分层作为网络初始化的参数。上图是AlexNet作者在16年的深度学习暑期学校时候课上的一页PPT。可以看出三种针对不同数据量级而选择的训练策略。之前做过的几次Kaggle比赛中，使用pre-trained model 和 train-from-scratch 拿到的性能结果差距不小. Alex讲到，对于在ImageNet上训练过的pre-trained model，其参数可以用来初始化别的任务：

数据量小的新任务。可以把前面的大部分层参数freeze，保留前面的卷积层和部分卷积层，以获取在ImageNet上得到的提取特征的能力，作为特征提取器，而只训练最后一层的全连接层。
数据量中等的新任务。则需要更多的可变的层来拟合新任务的数据，freeze前面的层，留出更多的层去拟合新数据。

但实际来说，什么是小和大往往没有定量的描述，我觉得还是需要根据pretrain模型时的数据和新问题的数据之间的多样性复杂程度来评估，只是说，可finetune的层数越多，可以拟合新数据的分布的参数越多，这一个观点。但若是认真去解决问题且时间充裕，需要把所有可能都尝试到。

“浅层学到的是纹理特征，而深层学到的是语义特征”，这句话是从某篇博文看到的，我认为网络层数在特征提取这里，单从可视化的角度来讲，如果是线性模型对学出的权重矩阵进行可视化，那么得到的是对应各类别图像的轮廓，这是CS231n课程有讲到的。然而上图是对GoogLeNet这一网络的特征图可视化的结果，可以看到浅层学到的是边缘（Edges）、纹理（Texture）等，深层学到的是更偏向语义的信息，相当于把原本线性模型的feature map拉长了。本质还是那么多信息，只是中间的过程更加清晰可见，看上图中最后一组6张图中第一列放大的图，有建筑物的特征，而且颜色偏蓝，应该是训练数据中该类的图像大多有云朵和天空作为建筑物的背景。

不过可以发现，无论网络深浅，最后一层（或几层）总是对应类别的轮廓，即语义信息。

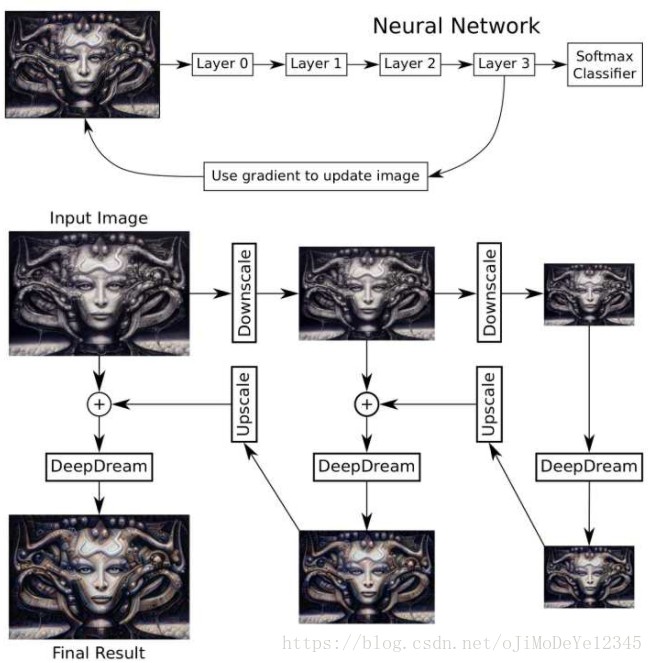
根据优化的目标不同，得到的可视化结果不同，如DeepDream就是对feature
map的结果backprop回去更新输入图像进行可视化（该过程的流程如下图，该图来自zhihu的一篇博客见参考部分。关于可视化这里我没有仔细看，需要结合Feature
Visualization这篇文章、Google Blog上关于DeepDream的两篇文章以及风格迁移学习那篇文章再深入分析）。

1.1.2 在其它数据集上的泛化性

作者通过在ImageNet预训练得到的模型，在其他小数据（VOC-2007、VOC-2012、Caltech-101、Caltech-256等图像分类任务）上发现优秀的泛化性能（这部分来自本篇文章附录 Localization 的 Generation of Very Deep Features），作者说到使用pre-trained模型，再在自己的小数据上训练不容易过拟合，关于这点我的理解是：

一开始在量级大且多样性广的数据集（如ImageNet）上pre-train，不严谨地说，新问题的小数据只是当初pre-train时所用数据集的一个子集，换句话说，pre-trained模型的参数已经避开了用小数据train-from-scratch的一些局部最优；
一开始在足够大的数据上pre-train，模型已经见识过了广阔的样本空间，这会带来了更广阔和丰富的特征空间，因而模型在小数据上学习时不会太过纠结于比较片面或者偏斜的样本带来的影响（还是类似第一点，初始化足够好）。

总而言之：事半功倍，pre-trained模型用于fine-tune前已经趟（略，或者说exploit）过了很多坑（局部最优），因而效果好。另外，作者还使用不同尺度跑网络的方式提取到多组特征，对它们做平均的方法来表示最终给分类器的特征，这样相比将特征直接concate，不会导致最终特征太多（inflating，或者说是膨胀）。另外，作者发现使用multi-scale训练模型时，如果尺度范围比较小（256，384，512，640，768和256，384，512 两种 multi-scale相比）提升的性能比较有限（0.3%）。

$$ x’_{i,j} = \frac{x_{i,j}}{\sqrt{ \sum_{i=0}^{height-1} \sum_{j=0}^{width-1} x_{i,j}^2 }} $$

作者在使用pre-trained模型的时候，是把用于喂给softmax前、产生1000维的最后一层全连接层去掉，使用倒数第二个全连接层产生聚合了位置和尺度的4096维图像特征，将这个特征做L2-normalization（上面公式便是图像上位于第 i 行 j 列的像素点 $x_{i,j}$ 经过L2-norm后的像素值 $x’_{i,j}$，需要注意的是这里是图像处理中 L2-normalize）后给SVM分类器训练 1VsALL 模型，提取特征的CNN没有做fine-tune操作。作者用倒数第二层的4096维的特征的考量是这个维度一定程度聚合了multiple location 和 scale 的信息，我觉得这个说法还是有些道理，一是网络有三个全连接层，经过1个或者2个全连接，原本的带有位置的局部信息被聚合起来了，但是 4096 维度的数目这个超参数还可以进一步使用交叉验证来优化，此外作者使用的是第二个fc后的特征，也不妨试试第一个fc后的特征、或者最后一个卷积的特征、甚至是将这些拼起来，说不定效果会更好。

此外，作者在对CNN提取到的特征做了聚合和一些变换，作者对4096维的resulting feature map（也就是刚做过l2-normalize过程的）再做global average pooling 产生一样维度的输出，并将与之镜像的图片也做同样的过程，最后将二者的特征加和求平均。当然全局平均池化（global average pooling，Network In Network有介绍该方法和dropout在作用上都起到正则作用，但有两个特点：1. 让feature map与类别通过softmax时的计算更自然，feature map也即对应类别的置信度分数；2. 无参数的策略，避免了过拟合问题。更多的参考上图NIN的截图）是一种聚合方法，作者也说到还可以使用stacking到一起，我想应该类似concate。

2. ConvNet Configurations

为了方便分析，先把VGGNet16的结构图放出来，即将说到的内容会跟下面这幅图有很密切的关系：

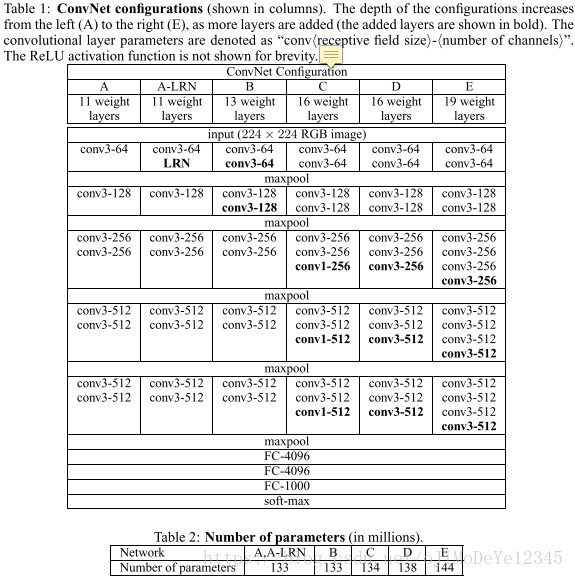
结合这张图，我们有网络D的参数表格（参数来自CS231n的计算，我这里重新排版）：

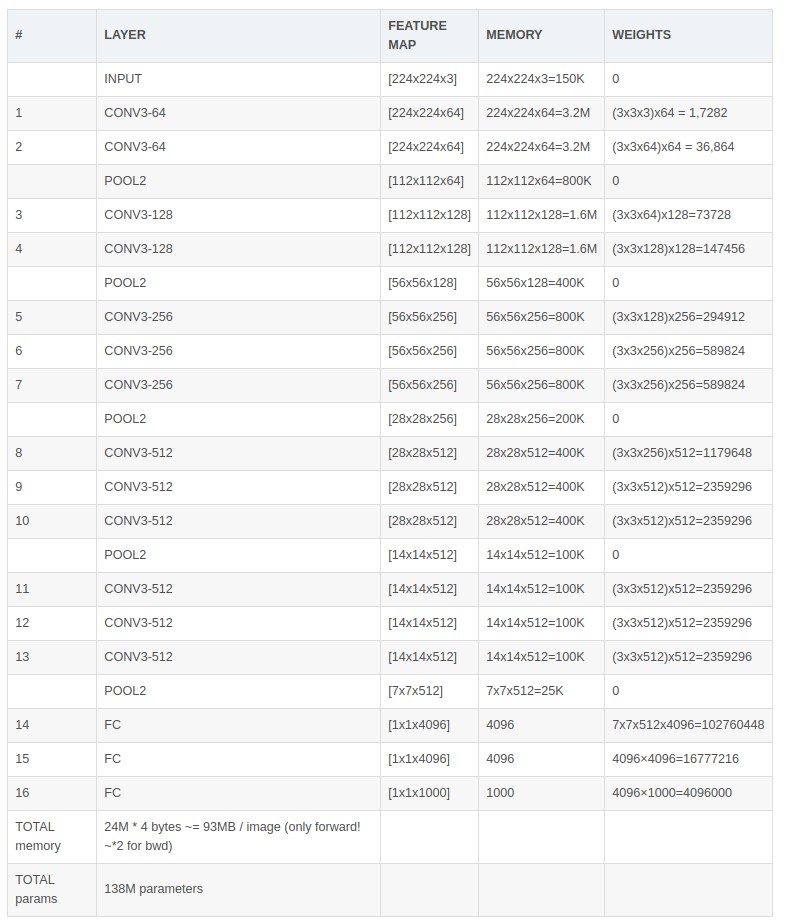
网络的输入尺寸为224×224的图像，输入前需要减去RGB均值（提前跑了一遍train set，resize到224并计算每个位置的强度均值）。下面是作者作的六组实验，观察深度、LRN、conv1x1的小卷积这三个因素对结果的影响（另外，也可以看出层数的算法，是只统计卷积层和全连接层）。

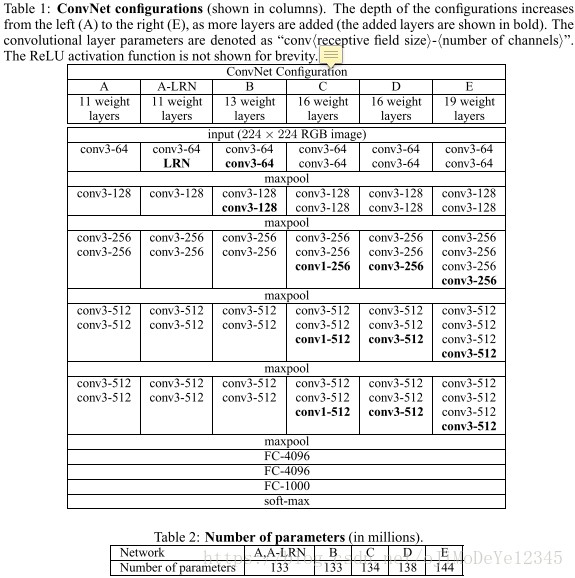
在具体说明结构之前，先说一下在AlexNet中出现的LRN（Local Response Normalization）层，该层会对相邻的N个通道在同一 (x,y) 位置处的像素值进行normalize。VGGNet作者发现（实验A和A-LRN），LRN层对分类准确率不仅没有提升，还带来更多的显存占用和计算时间，因此在之后的四组（B、C、D、E）实验中均没有出现LRN层。

观察上图6组实验中可以发现作者在统计层数的时候，不算POOL、LRN、softmax，只算conv、fc，比方A组中所有的fc层和conv层加起来是11，A组就是11层。我想这是因为：

参数太少。像relu、pool这样的层参数量太少，有的甚至如激活层relu不保存中间结果直接给下一层；
计算量小。相比conv甚至fc，pool这些层的计算量太少。

此外，所有实验中的网络结构除了层数大体相同，均是五组卷积（每一组可能有多个卷积层，A网络包含8个卷积，E网络包含16个卷积），再接三个全连接层。网络得到的feature map从64开始随卷积组数的推进逐渐递增，以2的倍率扩大直到达到512的channel数。因为小卷积核的缘故，网络即使很深也不会带来过大的参数量（见上图Table2）。

2.1 卷积

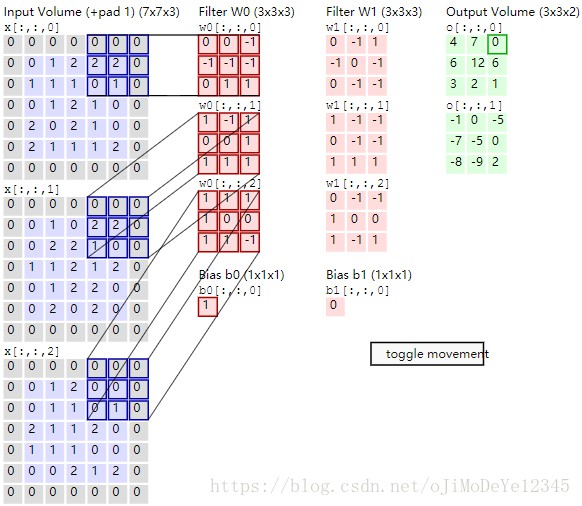
上图是卷积核在feature map上滑动的过程，这幅图来自CS231n。下面是Deep Learning for Computer Vision (Andrej Karpathy, OpenAI)暑期学校课上列出的卷积公式：
$f[x,y] \ast g[x,y] = \sum_{n_1=-\infty }^{\infty} \sum_{n_2=-\infty }^{\infty} f[n_1,n_2] \cdot g[x-n_1, y-n_2]$

但似乎这里的公式写错了，应该写成：
$f[x,y] \ast g[x,y] = \sum_{n_1=-\infty }^{\infty} \sum_{n_2=-\infty }^{\infty} f[n_1,n_2] \cdot g[n_1-x, n_2-y]$

在知乎的“如何通俗的理解卷积？”这个问题下，找到一个比贾扬清的回答更易于理解的一个回答，下面是该回答中的计算过程示意图：

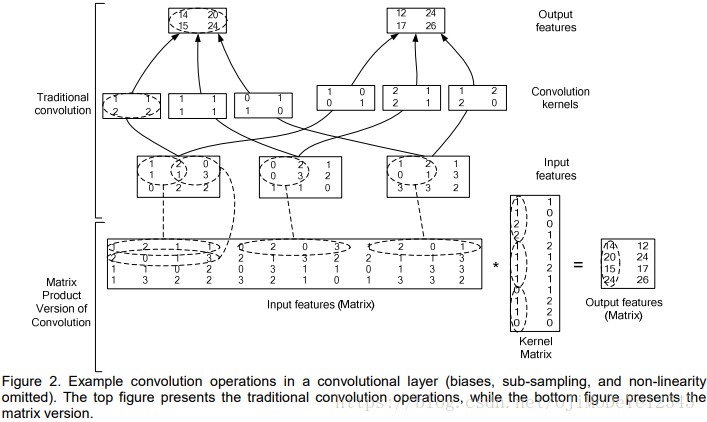
这幅图描述的是卷积的两种实现方式，上面的中括号Traditional convolution就是直接法实现卷积，而下面的 Matrix Product Version of Convolution则是使用矩阵乘法实现卷积，可以看到该方法会先对原图上卷积核2×2的大小的位置进行提取，也就是 im2col 的过程，在这里depth是 3，即三个通道，那么对输入的三通道图像的第一个计算卷积的位置处，会提取出2x2x3=12个元素成为一行，然后对所有的位置提取，多少个位置对应Input features (Matrix)的行数，而卷积核的个数对应kernel matrix的列数。刚好矩阵A（即Input features）的第一行和矩阵B（即Kernel Matrix）的第一列的结果就是结果矩阵第一个位置对应元素的结果，也就是卷积后的结果。

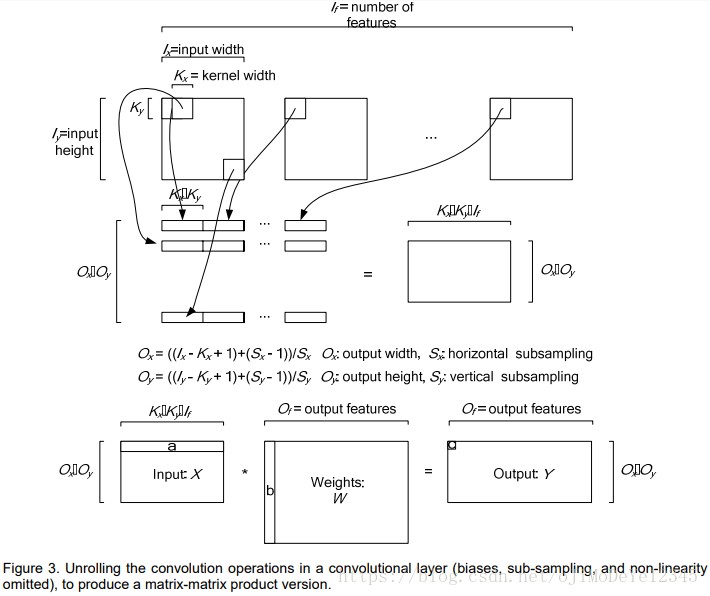
图就是进一步列成矩阵乘法的样子，进一步抽象并列出公式的示意图。矩阵A（Input matrix）的行数相当于下图卷积在原图上滑动的次数，列数就是 KxKxC，其中 K 和 C 分别是卷积核的宽/高、feature map的通道数（Channel/Depth）：

但需要注意的是，input matrix通常都是带有深度，或者说是厚度的（depth/channel），这个动态地在不同位置处卷积的过程也可用下图表示：

既然知道了卷积的做法，那么下面我将分析：

卷积核尺寸；
feature map的维度变化（height，width，depth）；
卷积组（相比AlexNet的变化及个人没有实验的感性分析）。

2.1.1 卷积核尺寸

说VGGNet的kernel size前，不妨先来看看AlexNet的kernel size，AlexNet的结构如下：

可以看出AlexNet虽然也有用3×3的卷积核，而且是大规模用，但基本上都是在网络的中后期。一开始却用了11×11这样的大卷积核，需要注意该卷积核对应的stride为4。我的理解是，一开始原图的尺寸虽然很大很冗余，但最为原始的纹理细节的特征变化一开始就用大卷积核尽早捕捉到比较好，后面的更深的层数害怕会丢失掉较大局部范围内的特征相关性，因为后面更多是3×3这样的小卷积核（和一个5×5卷积）。

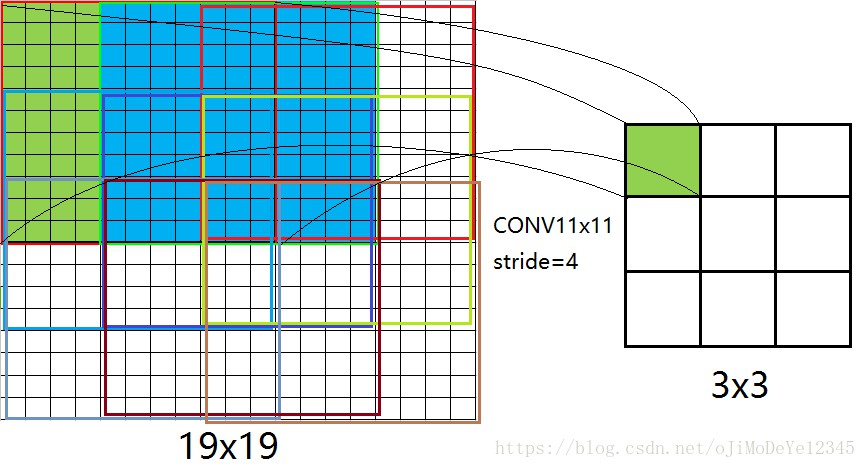
另外，conv11x11 这样的大卷积核使用的 stride 为4，见上图是我画的在一张 19×19 的图上做11×11的卷积，其实会发现即使是 stride 为4，对于11×11的kernel size而言，中间有很大的重叠，计算出的3×3区域每个值很过于受到周边像素的影响，每个位置卷积的结果会更多考虑周边局部的像素点，原始的特征多少有被平滑掉的感觉。换句话说，局部信息因为过大的重叠，会造成更多细节信息的丢失。那大卷积核，是否带来更大的参数和feature map大小呢？我计算了同样conv3x3、conv5x5、conv7x7、conv9x9和conv11x11，在224x224x3的RGB图上（设置pad=1，stride=4，output_channel=96）做卷积，卷积层的参数规模和得到的feature map的大小：

看来大卷积核带来的参数量并不大（卷积核参数+卷积后的feature map参数，不同kernel大小这二者加和都是30万的参数量），即使考虑AlexNet中有两种形式的卷机组（[conv-relu]-lrn-pool和[conv-relu]-[conv-relu]-[conv-relu]-pool）。实际增大的是计算量（上面我列出了计算量的公式，最后要乘以2，代表乘加操作）。为了尽可能证一致，我这里所有卷积核使用的stride均为4，可以看到，conv3x3、conv5x5、conv7x7、conv9x9、conv11x11的计算规模依次为：1600万，4500万，1.4亿、2亿，这种规模下的卷积，虽然参数量增长不大，但是计算量是恐怖的。

其实对比参数量，单层卷积核参数的量级在十万，一般都不会超过百万。相比全连接的参数规模是上一层的feature map和全连接的神经元个数相乘，这个也很恐怖。

作者在VGGNet的实验中只用了两种卷积核大小：1×1和3×3。作者认为两个3×3的卷积堆叠获得的感受野大小，相当一个5×5的卷积；而3个3×3卷积的堆叠获取到的感受野相当于一个7×7的卷积。见上图，输入的8个元素可以视为feature map的宽或者高，我画了当输入为8个神经元经过三层conv3x3的卷积得到2个神经元。

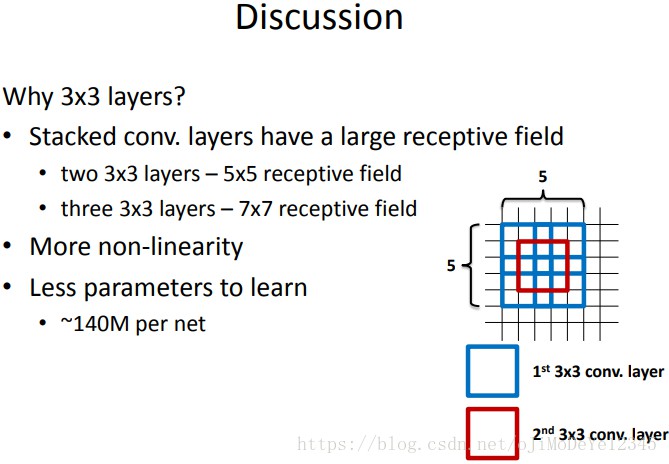
此外，在分割问题中卷积核的大小对结果有一定的影响，在上图三层的conv3x3中，最后一个神经元的计算是基于第一层输入的7个神经元，换句话说，反向传播时，该层会影响到第一层conv3x3的前7个参数。从输出层往回forward同样的层数下，大卷积影响（做参数更新时）到的前面的输入神经元越多。

input=8，3层conv3x3后，output=2，等同于1层conv7x7的结果；
input=8，2层conv3x3后，output=2，等同于2层conv5x5的结果。

上图是用2个stride=1、padding=0的conv3x3来代替1个stride=2的conv5x5的例子。此外，作者在3个conv3x3代替1个conv7x7的做法上，认为有以下三点优势：

3个激活函数（ReLU）去代替1个，可使决策函数更加具有辨别能力，此外就卷积本身的作用而言，3×3 比 7×7 就足以捕获特征的变化：3×3的9个格子，最中间的格子是一个感受野中心，可以捕获上下左右以及斜对角的特征变化。主要在于3个堆叠起来后，三个3×3近似一个7×7，网络深了两层且多出了两个非线性ReLU函数，（特征多样性和参数参数量的增大）使得网络容量更大（关于model capacity，AlexNet的作者认为可以用模型的深度和宽度来控制capacity），对于不同类别的区分能力更强（此外，从模型压缩角度也是要摒弃7×7，用更少的参数获得更深更宽的网络，也一定程度代表着模型容量，后人也认为更深更宽比矮胖的网络好）；

以下是个人的深层思考：网络更深带来了更多变化，更好的特征多样性，就好比是数据增强虽然引来方差是好的，我们想在变化中寻找不变的映射关系。但是，网络更深带来特征更多真的好嘛？我觉得更多的特征和更深的网络，不一定都是有助于、有贡献于正确梯度下降寻找最优或者局部最优的方向，我们真正需要的是可以正确建立映射关系的特征。
反倒是层数越深，特征更多，会有更多局部最优。但为此，我们又在减少因引入特征多样性带来的高方差的影响，不论是在随机梯度下降中引入动量，还是各种正则化的手段，又尝试减少更深网络带来更多特征造成的影响。一方面我们在增大方差，又在减少方差。这样看，似乎这是矛盾的。
网络由于有着本身的更新策略，可以正确建立映射关系。但网络更深却在影响映射关系的建立，把这个建立的过程变得更加曲折，甚至无法建立出好的、正确的、有效的映射关系。
我想了想，感觉这是一个平衡，重要是多了可以筛选：
一方面，我们希望有更多特征，在于我们可以筛选。本身的更新策略可以指导映射关系的建立。但是学习的东西多了，必然会造成学习出现问题，因为要在其中筛选。但是所有的基于部分样本的优化带来的梯度估计，必然会学出的权重都有一点不正确。
另一方面，我们又在减少影响，减少不正确性带来的影响，就有这些正则化来去筛选。有的正则化起到筛选的作用，而有的则是减缓、减小高方差带来错误下降方向的影响的作用。
我觉得重点在于这个特征筛选做的好不好，现在大多情况都不缺数据。其实这样看来，即使是深度学习，又回到了以前的问题，特征工程、特征选择。似乎深度学习带来了更深的网络，表面上看给我们造成没有必要做特征工程的假象，但其实我们做了这个过程，在网络结构设计、模块选择、网络的训练（优化）trick里。
无论是特征跨 depth 的 cross（resnet），还是跨channel的cross（lrn、shufflenet）。这几年的网络都是在网络更dense的前提（比方mobilenet）下，基于各自的module做特征工程，引入更多特征，一方面特征 diverse 方差加大，一方面又用正则等手段钝化平滑方差。我认为，大家认为深度学习玄学的一个原因可能是不可估量的方差的 tradeoff 造成的。
有小伙伴也提到，玄学也是因为现在的文章中说到的方法其实并不是work的，你按照他说的这么调整就是不对。

conv filter的参数减少。相比5×5、7×7和11×11的大卷积核，3×3明显地减少了参数量。作者还使用了1×1的卷积核，认为1×1卷积核是channel级别的线性变换（毕竟一组channel用对应的一样的卷积核在这一组channel上扫描，一组channel不是指这一层feature map的所有channel）。比方input channel数和output channel数均为C，那么3层conv3x3卷积所需要的卷积层参数是：3x(Cx3x3xC)=27C^2 ，而一层conv7x7卷积所需要的卷积层参数是：Cx7x7xC=49C^2。conv7x7的卷积核参数比conv3x3多了(49-27)/27×100% ≈ 81%；
小卷积核代替大卷积核有正则作用。作者用三个conv3x3代替一个 conv7x7，认为可以进一步分解（decomposition）原本用7×7大卷积核提到的特征.

This can be seen as imposing a regularisation on the 7 × 7 conv. ﬁlters,
forcing them to have a decomposition through the 3 × 3 ﬁlters (with
non-linearity injected in between).

我没看明白，关于正则化在《Deep Learning》这本书的Chapter 7 Regularization for Deep Learning中是这么定义的：

In section 5.2.2, we deﬁned regularization as “any modiﬁcation we make
to a learning algorithm that is intended to reduce its generalization
error but not its training error.”

也就是说，只要是可以减少泛化（验证集/测试集）误差，而非训练误差的任何方法都属于正则化。作者所说的分解（decomposition）我可以感性理解，但是认为这是一种正则化可能还需要做进一步关于 “小卷积替代大卷积的” ablation study 和理论证明。

选用 1×1 卷积核的原因：作者首先认为1×1卷积可以增加决策函数（decision function，这里的决策函数我认为就是softmax）的非线性能力，非线性是由激活函数ReLU决定的，本身1×1 卷积则是线性映射，即将输入的feature map映射到同样维度的feature map。作者还提到“Network in Network” architecture of Lin et al. (2014).这篇文章就大量使用了1×1卷积核。

此外，搜了些相关资料，简单总结下1×1卷积的特点（就不说加入非线性这个conv自带的特点了）：

专注于跨通道的特征组合：conv1x1 根本不考虑单通道上像素的局部信息（不考虑局部信息），专注于那一个卷积核内部通道的信息整合。conv3x3 既考虑跨通道，也考虑局部信息整合；
对 feature map 的channel级别降维或升维：例如224x224x100的图像（或feature map）经过20个conv1x1的卷积核，得到 224x224x20 的 feature map。尤其当卷积核（即filter）数量达到上百个时，3×3 或 5×5 卷积的计算会非常耗时，所以 1×1 卷积在 3×3 或 5×5 卷积计算前先降低 feature map 的维度。

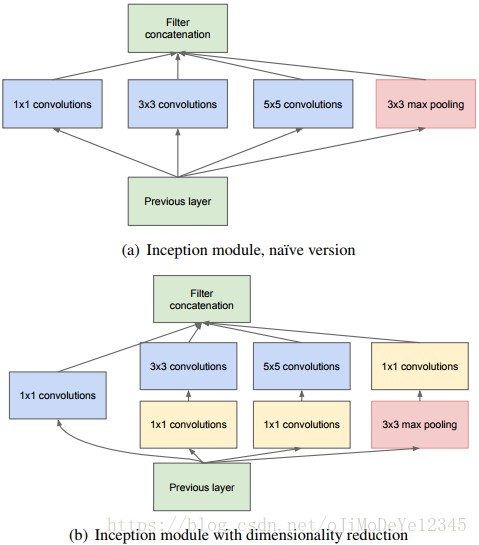
关于小卷积核前人就有使用，如Ciresan et al. (2011)还有Goodfellow et al. (2014)，后者使用11 层的网络解决街道数量的识别问题（street number classification，我也没看懂是回归还是分类），结果显示更深的网络可以带来更好地网络性能。而作者在小卷积核的基础上使用了更多层数，2014年ImageNet分类比赛的第一名使用GoogLeNet，Szegedy et al., (2014)也使用了更小的卷积核、更深达到22层的网络，使用了5×5、3×3和1×1卷积（实际还用到了7×7的卷积，第一层卷积）。但GoogLeNet的拓扑结构比较复杂，上图是Inception module的结构图，可以看到module内直接使用了常见的三种卷积核进行并联，并将最后的结果feature map直接concate到一起，而VGGNet则是使用传统卷积核串联的方式。

然而，分类性能上同样的单模型，VGGNet比GoogLeNet在top5的错分率要低，而多模型下，同样七个网络的VGGNet不如GoogLeNet。

2.1.2 feature map的维度变化

随层数递增逐渐忽略局部信息，feature map 的 width 和 height 随着每个pool操作缩小50%，5个pool 操作使得 width 和 height 逐渐变化：224->112->56->28->14->7，但是深度depth（或说是channel数），随着5组卷积在每次增大一倍：3->64->128->256->512->512。特征信息从一开始输入的224x224x3被变换到7x7x512，从原本较为local的信息逐渐分摊到不同channel上，随着每次的conv和pool操作打散到channel层级上。

我的理解是，这样便于后面fc层的特征映射，因为 fc 层相比conv更考虑全局信息，global的feature map（既有width，height还有channel）信息，全部映射到4096维度。估算一下，也就是说7x7x512，大概是25000，映射到4096，大概是5000，就是说压缩到原来的五分之一。后面三个全连接的理解是，这个映射过程的学习要慢点来，太快不易于捕捉特征映射来去之间的细微变化，让backprop学的更慢更细一些（更逐渐）。

其实按理说不应该将 feature map 的维度与后面 fc 层的分析拆分开，毕竟最后的分类器是softmax，三个fc层的操作结束才是最终的 feature map。那么，最后一组卷积后就会接三组全连接层，前两组fc的形式是：fc4096-relu-dropout0.5，最后一个fc的形式就是：fc1000。

可以发现feature map的维度在最后一个卷积后达到7x7x512，即大概25000，紧接着压缩到4096维，可能是作者认为这个过程太急，又接一个fc4096作为缓冲，同时两个fc4096后的relu又接dropout0.5 去过渡这个过程，因为最后即将给1k-way softmax，所以又接了一个fc1000去降低softmax的学习压力。

feature map维度的整体变化过程是：先将local信息压缩，并分摊到channel层级，然后无视channel和local，通过fc这个变换再进一步压缩为稠密的feature map，这样对于分类器而言有好处也有坏处，好处是将local信息隐藏于/压缩到feature map中，坏处是信息压缩都是有损失的，相当于local信息被破坏了（分类器没有考虑到，其实对于图像任务而言，单张feature map上的local信息还是有用的.）

2.1.3 卷积组

除了卷积kernel和feature map的变化，卷积后的output channel数的变化是递增的（上面已经说过）。但是，若以pooling操作为切分点对整个网络分组的话，我们会得到五组卷积，五组卷积中有2种卷积组的形式，VGG网络是下面这样：

前两组卷积形式一样，每组都是：conv-relu-conv-relu-pool；
中间三组卷积形式一样，每组都是：conv-relu-conv-relu-conv-relu-pool；
最后三个组全连接fc层，前两组fc，每组都是：fc-relu-dropout；最后一个fc仅有fc。

CS231n的blog里将这种形式称为layer pattern，一般常见的网络都可以表示为：INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC的形式，其中，?表示pool是一个可选项。这样的pattern，因为可以对小卷积核stacking，更适合构建深层网络。INPUT -> FC表示一个线性分类器。

那么这VGG两种卷积组，即layer pattern的形式有什么区别，很明显第二种（[conv-relu]-[conv-relu]-[conv-relu]-pool）比第一种（[conv-relu]-[conv-relu]-pool）多了一个[conv-relu]。我的理解是：

多出的relu对网络中层进一步压榨提炼特征。结合一开始单张 feature map 的 local 信息更多一些，还没来得及把信息分摊到 channel 级别上，那么往后就慢慢以增大 conv filter 的形式递增地扩大channel数，等到了网络的中层，channel数升得差不多了（信息分摊到channel上得差不多了），那么还想抽 local 的信息，就通过再加一个[conv-relu]的形式去压榨提炼特征。有点类似传统特征工程中，已有的特征在固定的模型下没有性能提升了，那就用更多的非线性变换对已有的特征去做变换，产生更多的特征的意味；
多出的conv对网络中层进一步进行学习指导和控制不要将特征信息漂移到channel级别上。
1. 上一点更多的是relu的带来的理解，那么多出的[conv-relu]中 conv 的意味就是模型更强的对数据分布学习过程的约束力/控制力，做到信息backprop可以回传回来的学习指导。本身多了relu特征变换就加剧（权力释放），那么再用一个 conv 去控制（权力回收），也在指导网络中层的收敛；
2. 其实 conv 本身关注单张feature map上的局部信息，也是在尝试去尽量平衡已经失衡的channel 级别（depth）和local级别（width、height）之间的天平。这个conv控制着特征的信息量不要过于向着channel级别偏移。

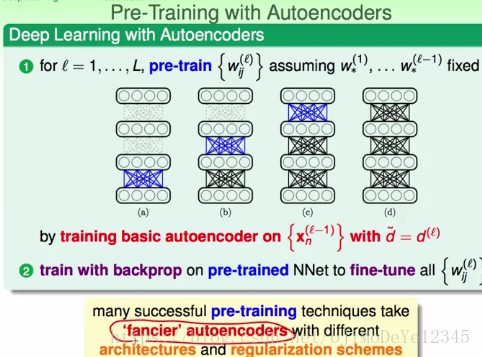
其实说到这里，我想到一种古老的pretrain网络的方式（见上图，来自台大的机器学习技法课程）：使用 auto-encoder 和 decoder 去逐层预训练网络，逐层地用输入 x 预测输入 x 。虽然说和这里的卷积组的形式还是差异比较大，但是逐渐逐层地去学习的意思在里面。逐层的预训练网络，在我理解就是想通过这样的方式训练处能够提取深层特征表征的网络权重。多少有点类似（其实有点牵强）这里更深的一种卷积组的感觉，类比一下，每次我都在训练一种卷积组，第一次可能是一层的卷积，第二次是两层的，第三次是三层的，依此类推。我既希望这样保证学到的权重不会导致结果发散（爆炸或者消失），也希望可以有足以让当前层特征传递到下一层、维持高效表示的特征权重（重点在于这一点）。

关于卷积组（Layer pattern），CS231n的博客给出如下观点：

串联和串联中带有并联的网络架构。近年来，GoogLeNet在其网络结构中引入了Inception模块，ResNet中引入了Residual Block，这些模块都有自己复杂的操作，上图就是Inception模块。换句话说，传统一味地去串联网络可能并不如这样串联为主线，带有一些并联同类操作但不同参数的模块可能在特征提取上更好。
所以我认为这里本质上依旧是在做特征工程，只不过把这个过程放在里 block 或者 module 的小的网络结构里，毕竟 kernel、stride、output 的大小等等超参数都要自己设置，目的还是产生更多丰富多样的特征。
用在 ImageNet 上 pre-trained 过的模型。设计自己模型架构很浪费时间，尤其是不同的模型架构需要跑数据来验证性能，所以不妨使用别人在 ImageNet 上训练好的模型，然后在自己的数据和问题上在进行参数微调，收敛快精度更好。
我认为只要性能好精度高，选择什么样的模型架构都可以，但是有时候要结合应用场景，对实时性能速度有要求的，可能需要多小网络，或者分级小网络，或者级联的模型，或者做大网络的知识蒸馏得到小网络，甚至对速度高精度不要求很高的，可以用传统方法。

2.1.4 Layer Sizing Patterns

要说到layer pattern，不得不提到 sizing pattern，这也是CS231n里所讲到的。对于每种层，有不同的默认设定：

输入层：大都是 2 的N次方，这和网络中卷积或者池化层出现的 stride 为 2 的次数有关，比方VGGNet中每个 pattern 的卷积不会对 feature map 的宽度和高度有改变，而每个pattern结束前总会做一个 stride 为 2 的下采样，因为有 5 组，那么做 5 次就是 32，所以VGGNet网络input大小一般都是 32 的倍数，即 $a \times 2^n$，$n$ 是下采样的次数，$a$ 是最终卷积和池化得到的feature map大小，如224或者384。

其实对于边界问题的处理，主要有4种方法：

用0填充，相当于黑色，卷积核对应位置相乘也是0；
用边界的邻近像素扩展；
把图当做一个循环，同一行最右边的填补使用最左边的像素；
舍弃无法卷积的部分。

卷积层：现在常用的是小卷积核如 3×3 或者 1×1。卷积为了保留feature map不变，通常会采取 pad 为 1 的操作，其实具体来说应该是：为了保证卷积后的 feature map的宽度和高度不变，那么有 $pad=(F-1)/2$，但我觉得这个有点问题，可以改成更一般的形式，不过首先可以看看计算下一层feature map宽高的公式：
$W_2 = (W_1 – F + 2P) / S + 1$

因为要保证$W_1$和$W_2$一样，有 $W_1=W_2=W$，那么可以导出：
$P = \frac{S(W-1) – W + F}{2}$
当 Stride=1 时，那么$pad=(F-1)/2$。因为现在 stride=1 的3×3卷积用的多，所以大家会默认说是 pad=1.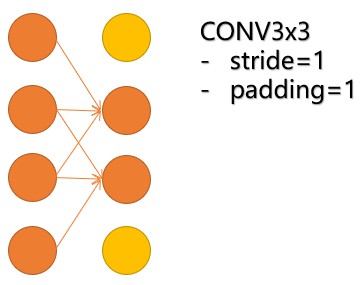

上图就是stride=1、padding=1的conv3x3的效果图。关于这点上，也是由于实验发现这样保留feature map 的宽高情况下，性能好的缘故，我认为填补主要是针对stride大于1的情况带来的边界问题，如果input尺寸不是事先设定的 $a \times 2^n$，那么就会有边界无法卷积到的问题带来信息丢失。不过这种填补我认为也有一定问题，就是说原本 conv3x3 去计算对应位置的 3×3，而填补后为0，这样相当于少算了一些值，这肯定还是有影响的。但若stride不是1，那么要保证前后feature map的宽高一样，就要根据上面的公式计算得出。
另一个点是通常与 Input 比较接近的 conv 会采用大卷积核。关于接近input层使用较大的卷积核这点，我认为先是考虑到后面的操作，先尽可能用大的卷积核 cover 更多的原始信息（虽然经过了卷积有一些变换），第二点在于大卷积核带来的大感受野，后面的卷积层能的一个神经元能看到更大的 input，第三点是GPU的显存受限，经典的例子就是 AlexNet 使用 stride=4 的 conv11x11，目的就是从一开始就减少显存占用，其实这里的大stride，我觉得起到了一些正则的作用。但缺点也很明显，因为卷积核变大，矩阵乘法实现卷积时，若没有大 stride，那么第一个矩阵的列数，也就是第二个矩阵的行数，会变大，带来大的计算量。所以在AlexNet中，大卷积核也对应使用了大的stride值；

池化层：常见2×2的max-pooling，少见3×3或者更大的kernel。更大的kernel带来的问题是信息丢失带来的信息损失，此外，stride通常为2；其实按照以上的设定看来，也是有好处的。卷积专注于保留空间信息前提下的channel变换，而池化则专注于空间信息的变换（下采样）.

2.2 池化

VGGNet 中的 max-pool 均采用kernel为2×2的尺寸，stride为2的设定。这里和AlexNet有区别，AlexNet使用的max-pool的kernel为3×3大小，stride为2的pool。

那么我想卷积核也可以是2×2、4×4这种偶数的吧，为什么大家都用奇数呢？我问了些人他们的回答也是说感受野中心这个问题。其实我觉得感受野中心看怎么理解，如果是4×4的卷积核，可以说 4×4 因为是偶数，中间没有感受野中心，但是也可以说 4×4 有 4 个感受野中心，也可以捕捉上下左右的信息，说不定效果比 3×3 还更好！在计算上，也是对应位置相乘后整体加，不过当前大家都在用奇数尺寸的卷积核，但这需要进一步实验说明。

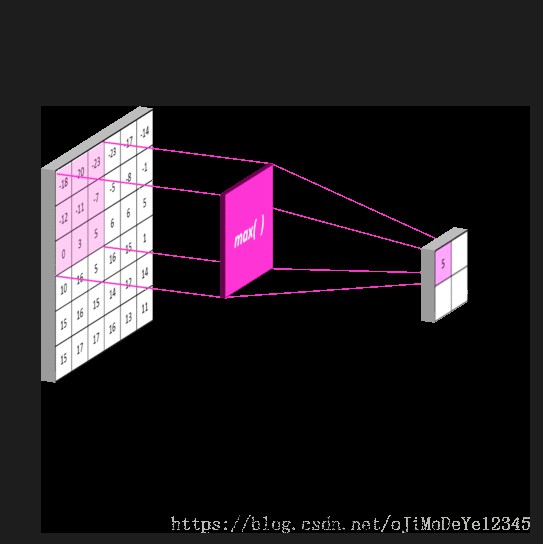
另外一个是池化，先前没有注意到 AlexNet 的 pooling 的kernel size全是奇数，里面所有池化采用kernel size为3×3，stride为2的max-pooling。而VGGNet所使用的 max-pooling的kernel size均为2×2，stride为2的max-pooling。pooling kernel size从奇数变为偶数。小kernel带来的是更细节的信息捕获，且是 max-pooling 更见微的同时进一步知著（见微知著，微:隐约；著:明显。意指看到微小的苗头，就知道可能会发生显著的变化。比喻小中见大、以小见大）。

在CS231n里讲到现在也在逐渐不使用 pooling，因为发现完全可以使用一个 stride 不等于1的卷积来代替pooling，另外，不少工作，如生成模型（generative models）、对抗网络（adversarial networks）、变分自动编码器（variational autoencoders ，VAEs），发现用stride不等于1的卷积来代替 pooling 带来的优势。

关于pooling反向传播的做法，常见有三种方式（max、average、stochastic，第三种随机池化现在已经不常见，训练过程的做法是将池化 kernel 位置中的原图的像素值，按照像素值占整体 kernel的比例来表示原始值，那么原始像素值大的被选中的概率也就越大，随机产生一个数看落到哪个区间就使用哪个点做下采样，而测试时的做法是每个位置的像素值乘以该位置的概率值并加和），caffe 代码中对第三种方式并没实现（可以提个PR，哈哈），反向的计算如下：

max：反向过程会记录当时正向时最大值的位置，反向则最大值位置不变，其他位置填补0；
average：反向过程会将正向的平均值，以平均的形式分摊到每个位置；
stochastic：反向一样记录正向时时被随机选中的位置，该位置值不变，其他位置填补0。

2.3 全连接

形式上完全平移AlexNet的最后三层，VGGNet后面三层（三个全连接层）为：

FC4096-ReLU6-Drop0.5，FC为高斯分布初始化（std=0.005），bias常数初始化（0.1）
FC4096-ReLU7-Drop0.5，FC为高斯分布初始化（std=0.005），bias常数初始化（0.1）
FC1000（最后接SoftMax1000分类），FC为高斯分布初始化（std=0.005），bias常数初始化（0.1）

超参数上只有最后一层fc有变化：bias的初始值，由AlexNet的0变为0.1，该层初始化高斯分布的标准差，由AlexNet的0.01变为0.005。超参数的变化，我的理解是，作者自己的感性理解指导认为，我以贡献bias来降低标准差，相当于标准差和bias间trade-off，或许作者实验validate发现这个值比之前AlexNet设置的（std=0.01，bias=0）要更好。

2.4 其它

我发现 AlexNet 和 VGGNet 的 SoftMax 层最后都是 1000 个输出，但是有小伙伴说，经常有不在这1000类里的物体被分类到了这一千类中的某一类，可能置信度还很高如80%等等，那我想在训练的过程中加一个背景这一类进行输出，这样用一些非 1000 类物体中的图片去训练。有小伙伴实验表示，这样性能会有小的提升。其实我们在一些分割或检测问题中，也见过不少作者是用原本的类别数加一类背景类去训练。

3. 训练和测试

实现是基于Caffe框架，作者 branch out 出一个caffe的分支，在一台4张NVIDIA Titan BLACK 的机器上完成的，梯度的计算是汇总多张卡同步后的结果，因此和在单GPU上训练的结果是一致的（4张卡相比单张有3.75倍的加速），训练一个网络根据架构的不同大概要2到3周的时间。

3.1 训练阶段

除了对训练图像的多尺度后的crop进行采样训练，其它和AlexNet基本一致：

优化方法：带动量（momentum）的小批量梯度下降
batch size：256
learning rate：0.01
和AlexNet一样，当val-acc 不下降则学习率缩小十倍，训练过程缩小了三次
momentum：0.9
weight decay（$L_2$惩罚乘子）：$5 \times 10^{-4}$
dropout rate（前两个全连接层）：0.5
目标函数：多项式逻辑斯特回归（SoftMax）
迭代次数：37万次iteration（74 epochs）后，停止训练

AlexNet的模型参数量是4000万（无论是one-gpu还是two-gpu版），feature map的量级在140万。AlexNet训练了90个 epochs，用了两张GTX 580 3GB跑了5、6天，估算下来230img/sec/2gpus；而VGGNet的6个模型的参量级都在1亿3000万到1亿4000万之间，feature map我没算，四张卡跑一个网络大概是2到三周的时间，假设两周半，那么估算下来62.64img/sec/4gpus。

尽管模型参数量是AlexNet的3倍多且层数深，但跑的epochs比AlexNet少收敛快，作者认为是以下两点原因：

正则化：dropout和小卷积核的使用。关于dropout，我记得AlexNet有写道：前两个全连接层用到了dropout，若没有dropout模型必然会过拟合，但是有dropout后，收敛大约需要原本两倍的 iteration 次数。我对 dropout 的理解是模型 ensemble，每次iteration对原网络dropout 一些神经元后的模型可视为一个单独的模型，最后test时则是ensemble的模型，效果必然好于单模型。参数越多越容易过拟合，比方全连接层比卷积层要容易过拟合，全连接层因为参数量大，好比一个多元高次函数，而卷积层好比简单的函数，多元高次的函数肯定在捕捉细节特征上会比简单函数好，但代价就是训练时间更长，需要正则化等方法去平衡。对于收敛更快，我认为主要是小卷积核带来的优势，小卷积核参数少，从训练样本中需要拟合/学习的参数自然少，而且backprop的时候涉及到前面的范围也比较小，因而似乎会收敛快（但我不认为这是 VGG 比 AlexNet 收敛快的根本原因）；
pre-initialisation，相当于预训练。为了防止不好的初始化会导致训练过程中停止学习，作者把A实验的模型的前四个卷积层和三个全连接层的参数拿来作为模型的初始化参数，中间层的初始值从均值为0，方差为0.01的正态分布中采样得到，bias初始化为0，学习率设定和训练A（相当于pre-train）时的一样。虽然作者没有承认pre-initialisation是预训练，但本质上就是。好处主要两点：性能比train-from-scratch有提高，且收敛更。

作者对中间层以均值为0，方差为0.01的正态分布初始化，和AlexNet一样。我想也可以对已经训练过的网络做权重值的统计，用统计出的分布去尝试初始化网络层。作者最后也说到，提交结果后，Glorot& Bengio (2010)等人使用随机初始过程来对模型做参数初始化。

其实我想说，收敛更快的主要原因很可能就是预训练，说小卷积核和dropout有点扯，感觉正则只会延长训练过程。另外在知乎看到一个观点很有意思：

便也要纠正一下在提到CNN的时候经常出现的错误：“CNN的参数太多，造成学习困难。”
其实CNN相比较于以前的模型，参数并不见得多：在CNN之前，NEC Labs 采用 sparse SIFT＋Pyramid Pooling的方法取得过ILSVRC的冠军，在这些模型中，最后线性SVM的输入特征在160K 到 260K不等。因为一共有1000类，所以SVM的总参数是160M－260M左右。Alex 2012年的模型只有60M参数，而我们今年的模型大概只有7M。（补充编辑：这些图像特征一般都是稀疏的，但是SVM的参数并不稀疏。）
所以，其实我们应该说的是，CNN的优化是一个非凸（non-convex）的问题，所以才比较困难.
参考：如何评价今年的 ILSVRC 2014 结果？
https://www.zhihu.com/question/24904450

3.1.1 训练图像尺寸

模型输入的固定input大小是 224×224，这个大小的图是由rescale后的训练图像随机crop得到的（rescale是VGGNet的特色，后面会详细讲到），（即使是同一张图像）每次SGD的iteration的crop都不同。为了进一步data augmentation，在crop上又做了随机水平翻转（random horizontal flipping）和随机的RGB颜色抖动，这两个小技巧也都来自AlexNet.

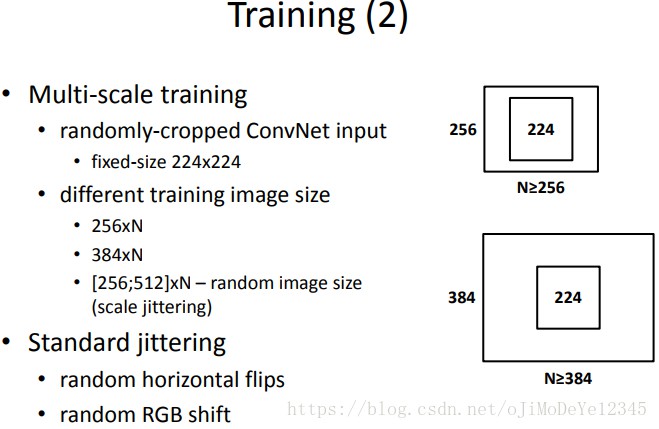
设置 S 是rescale后的训练图像的短边，用 S 代指训练过程使用的尺度。但crop的大小是固定的：224×224。总之 S 不小于224，但当 S=224 时，因为长边大于等于224,，所以 crop 尺寸可以大体上捕捉整幅图片。而当训练的图像尺度S远远大于224时，crop 将只会对应图像的一小部分或者某些物体的部分。

作者使用两种方法设置训练图像的尺度S：

固定训练图像的最短边S，用这种单一尺度去训练。即使是短边固定了，但依然对原图 crop 得到多种尺度的信息。作者使用S=256（借鉴AlexNet等人）和S=384。作者先用 S=256 crop出的图像去训练网络，之后再用 S=384 crop出的图像去fine-tune网络（该过程用了比S=256时更小的学习率0.001）；
多种短边尺度S训练。给定S的一个范围，作者使用[256, 512]。这样带来的好处是需要分类或者 localize 的物体本身在图像上的像素就不同，这样在训练中就把这一因素考虑进去。这也可以看做是 data augmentation 里的尺度扩增（scale jittering），这样训练同一个模型时是基于不同尺度的图像进行的。作者依然是为了speed reason（太假了，明显是因为fine-tine效果好，还不承认），基于model A 去 fine-tune了所有层。但是pre-train mode是采用固定尺寸384的最短边的训练图像crop出的224的图，去train-from-scratch的.

3.2 测试阶段

测试阶段先对输入图像的短边rescale到预设尺度Q（测试图像的尺度），测试图像的尺寸Q和训练图像的尺寸 S 没必要完全一样。后文中作者提到对于每个训练图像的尺寸S，都有几个不同的Q来去预测，可以得到更好地性能。

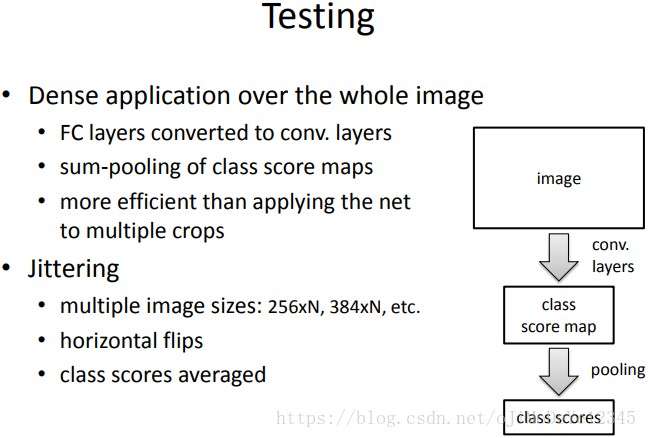
原图比方左上角有个 5×5 的区域，crop出的224×224的左上角可以在里面移动（也就是说图像crop前，要resize到可以移动5×5格子的size，即224+5-1=228），另外加上水平翻转带来的可能性，那就是5x5x2=50种情况，作者总共在test阶段用了三个scale，即三个Q，那么一张图总共有150 crops。网络将会分别跑一张图的150个crops，然后将结果average，作者的150crops相比GoogLeNet（Szegedy et al. (2014)）的 4 scale的 144 crops（可以算一下，每个scale是36crops，如果其中包含水平翻转的话，那么就是18crops，可能是一个3×6的 regular grid，类似的方法，因为没看文章这里只是猜测），并没有很大的性能提升。

3.2.1 全连接转为卷积

下面这段来自作者原文test小节的具体流程：

At test time, given a trained ConvNet and an input image, it is classified in the following way.
First, it is isotropically rescaled to a pre-defined smallest image side, denoted as Q (we also refer to it as the test scale). We note that Q is not necessarily equal to the training scale S (as we will show in Sect. 4, using several values of Q for each S leads to improved performance).
Then, the network is applied densely over the rescaled test image in a way similar to (Sermanet et al., 2014). Namely, the fully-connected layers are first converted to convolutional layers (the first FC layer to a 7 × 7 conv. layer, the last two FC layers to 1 × 1 conv. layers). The resulting fully-convolutional net is then applied to the whole (uncropped) image. The result is a class score map with the number of channels equal to the number of classes, and a variable spatial resolution, dependent on the input image size.
Finally, to obtain a fixed-size vector of class scores for the image, the class score map is spatially averaged (sum-pooled).
We also augment the test set by horizontal flipping of the images; the soft-max class posteriors of the original and flipped images are averaged to obtain the final scores for the image.

其中比较特别的一点在这句：

Namely, the fully-connected layers are first converted to convolutional layers (the first FC layer to a 7 × 7 conv. layer, the last two FC layers to 1 × 1 conv. layers).

也就是说，作者在测试阶段把网络中原本的三个全连接层依次变为 1 个conv7x7，2 个 conv1x1，也就是三个卷积层。改变之后，整个网络由于没有了全连接层，网络中间的feature map不会固定，所以网络对任意大小的输入都可以处理，因而作者在紧接着的后一句说到： The resulting
fully-convolutional net is then applied to the whole (uncropped) image。

上图是VGG网络最后三层的替换过程，上半部分是训练阶段，此时最后三层都是全连接层（输出分别是4096、4096、1000），下半部分是测试阶段（输出分别是1x1x4096、1x1x4096、1x1x1000），最后三层都是卷积层。下面我们来看一下详细的转换过程（以下过程都没有考虑bias，略了）：

先看训练阶段，有 4096 个输出的全连接层FC6的输入是一个 7x7x512 的feature map，因为全连接层的缘故，不需要考虑局部性，可以把 7x7x512 看成一个整体，25508（=7x7x512）个输入的每个元素都会与输出的每个元素（或者说是神经元）产生连接，所以每个输入都会有 4096 个系数对应4096个输出，所以网络的参数（也就是两层之间连线的个数，也就是每个输入元素的系数个数）规模就是 7x7x512x4096。对于FC7，输入是4096个，输出是4096个，因为每个输入都会和输出相连，即每个输出都有4096条连线（系数），那么4096个输入总共有4096×4096条连线（系数），最后一个FC8计算方式一样，略。

再看测试阶段，由于换成了卷积，第一个卷积后要得到 4096（或者说是1x1x4096）的输出，那么就要对输入的 7x7x512的feature map的宽高（即width、height维度）进行降维，同时对深度（即Channel/depth维度）进行升维。要把 7×7 降维到1×1，那么干脆直接一点，就用 7×7 的卷积核就行，另外深度层级的升维，因为 7×7 的卷积把宽高降到 1×1，那么刚好就升高到4096就好了，最后得到了 1x1x4096 的feature map。这其中卷积的参数量上，把 7x7x512 看做一组卷积参数，因为该层的输出是4096，那么相当于要有4096组这样 7x7x512 的卷积参数，那么总共的卷积参数量就是：[7x7x512]x4096，这里将 7x7x512 用中括号括起来，目的是把这看成是一组，就不会懵。

第二个卷积依旧得到 1x1x4096 的输出，因为输入也是 1x1x4096，三个维度（宽、高、深）都没变化，可以很快计算出这层的卷积的卷积核大小也是1×1，而且，通道数也是4096，因为对于输入来说，1x1x4096 是一组卷积参数，即一个完整的 filter，那么考虑所有4096个输出的情况下，卷积参数的规模就是 [1x1x4096]x4096。第三个卷积的计算一样，略。

其实VGG的作者把训练阶段的全连接替换为卷积是参考了OverFeat的工作，如下图是OverFeat将全连接换成卷积后，带来可以处理任意分辨率（在整张图）上计算卷积，而无需对原图resize的优势。

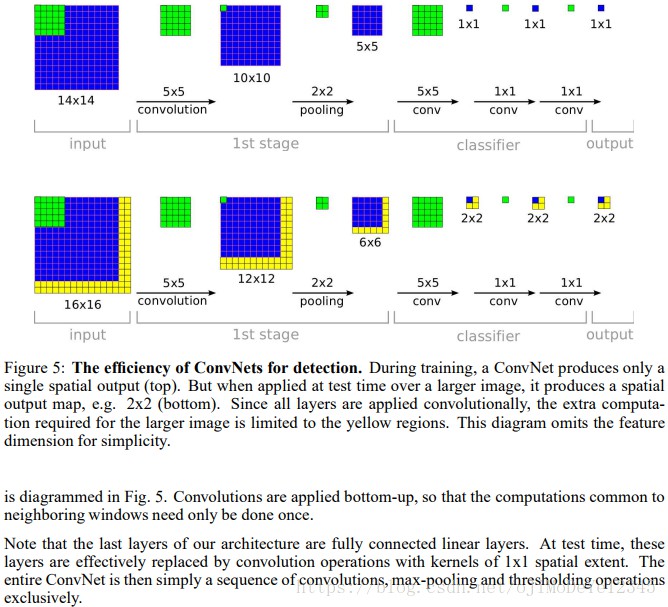
不过可以看到，训练阶段用的是 crop 或者 resize 到14×14的输入图像，而测试阶段可以接收任意维度，如果使用未经crop的原图作为输入（假设原图比crop或者resize到训练尺度的图像要大），这会带来一个问题：feature map变大了。比方 VGG 训练阶段用224x224x3的图作为模型输入，经过5组卷积和池化，最后到7x7x512维度，最后经过无论是三个卷积或者三个全连接，维度都会到1x1x4096->1x1x4096->1x1x1000，而使用 384x384x3 的图做模型输入，到五组卷积和池化做完（即$2^5=32$），那么feature map变为12x12x512，经过三个由全连接变的三个卷积，即feature map 经历了 6x6x4096->6x6x4096->6x6x1000 的变化过程后，再把这个 6x6x1000 的 feature map 最终交给SoftMax进行分类。

此外，我有想到四个问题：

文中说对 class score 做 average，但并未说这个 class score 是在 softmax 前还是后得到的。具体而言，作者在这里没有具体说明是将6x6x1000的 feature map 先做average到 1x1x1000 的维度后再做 SoftMax，还是先给 SoftMax 分类，得到 6x6x1000 的结果，再对每个结果进行average？因为作者没有说清楚，不过我觉得两个都可以试试，看哪种效果好用哪个。后来我想到 softmax 前必须是1k维的，因为 softmax 只是一个 soft-max，具体可以看看softmax的公式，这一来如果是 6x6x1000 的 feature map 需要在 softmax 前做 average 到 1x1x1000 才行；
直接把训练阶段的全连接参数当做测试阶段的卷积参数，不需要做参数微调嘛？做和不做，哪个效果更好？不过我可以想来如果用同样数据，效果可能不好或者持平，但是解决不同的问题或许再做 fine-tune，效果说不定会更好；
有实验表明将最后所有FC层转为CONV后，比方 384x384x3 的图，最后得到 6x6x1000 的feature map 与不转换 fc 为 conv 的单个网络跑36次，效果会更好嘛？
单个网络模型下，同样或者不同尺寸的图输入到转换前和转换后的网络，全卷积网络的性能更好吗？

以上问题都需要做实验才能得出，最近懒得动，也就捂脸不多说了。

4. 分类实验

12年到14年的挑战赛都使用的是 1000 个类别的ILSVRC-2012数据集（Large Scale Visual Recognition Challenge），其中：

训练集：130万张图片；
验证集：5万张图片；
测试集：10万张图片，这组数据的label没有给出（with held-out class labels）。

两个性能评估准则：top-1 和 top-5 error。前一个是多类分类错误率，错分的图像的比率。后一个是ILSVRC中主要的评估指标，计算的是预测出来的top5的类别里没有ground truth的比率，即top-5 error。

因为作者自己在下面实验的缘故，当然没有测试集的 ground truth 类别，所以作者就用验证集当做测试集来观察模型性能。这里作者使用两种方式来评估模型在测试集（实际的验证集）的性能表现：single scale evaluation 和 multi-scale evaluation。

4.1 单尺度评估

对每个网络（总共六个）进行单独评估，测试图像尺寸依训练时的尺寸设定分为两种情况：

训练图像的尺寸S固定时，设置训练图像尺寸S等于测试图像尺寸Q；
训练图像尺寸S是介于$[S_{min}, S_{max}]$时，设置测试图像尺寸$Q=0.5(S_{min}+S_{max})$。

作者发现，即使是单一尺度（Scale），训练时进行尺度随机（scale jittering）resize再crop图像（$S \in [256; 512]$）的方式比固定最小边后crop图片（S=256或者S=384）去训练的效果好。也再次印证了对训练图像以scale jittering的方式做augmentation（捕捉多尺度信息上）是有效果的。

实验结论：

LRN层无性能增益（A和A-LRN）。作者通过网络A和A-LRN发现AlexNet曾经用到的LRN层（local response normalization，LRN是一种跨通道去normalize像素值的方法）没有性能提升，因此在后面的4组网络中均没再出现LRN层。
当然我也感觉没啥用，想到 max-pooling 比 average-pooling 效果好，我就感觉这个LRN没啥用，不过如果把 LRN 改成跨通道的 max-normal，我感觉说不定会有性能提升。特征得到retain更明显。
深度增加，分类性能提高（A、B、C、D、E）。从11层的A到19层的E，网络深度增加对top1和top5的error下降很明显，所以作者得出这个结论，但其实除了深度外，其他几个网络宽度等因素也在变化，depth matters 的结论不够 convincing。
conv1x1的非线性变化有作用（C和D）。C和D网络层数相同，但D将C的3个conv3x3换成了conv1x1，性能提升。这点我理解是，跨通道的信息交换/融合，可以产生丰富的特征易于分类器学习。conv1x1相比conv3x3不会去学习local的局部像素信息，专注于跨通道的信息交换/融合，同时为后面全连接层（全连接层相当于global卷积）做准备，使之学习过程更自然。
多小卷积核比单大卷积核性能好（B）。作者做了实验用B和自己一个不在实验组里的较浅网络比较，较浅网络用conv5x5来代替B的两个conv3x3。多个小卷积核比单大卷积核效果好，换句话说当考虑卷积核大小时：depths matters。
非常非常感谢严谨的Ant同学，这里第四个结论的描述不够严谨及结论表述不清导致的这个错误。原文中说到：在同样感受野范围下，用5×5的卷积去等效替代3×3卷积的网络性能下降。因而我得出“多小卷积核比单大卷积核性能好”这一结论。这一结论我描述的不够严谨，应该改为：“多个小卷积核的堆叠比有同样感受野规模的大卷积性能好。”

然而另一点是我没有仔细看原文造成的。在原文中刚刚那个结论后的描述前有一句：it is also important to capture spatial context by using conv. filters with non-trivial receptive fields (D is better than C).，也就是说，还有一组实验是同样深度为16层的网络C和网络D的比较。网络C在5个组卷积的后3个组卷积中，每个组卷积中的最后一个卷积都是1×1卷积（而网络D均为3×3卷积），性能不如网络D。这恰恰是一个1×1的卷积核性能要比3×3的大卷积性能差的对照组。与我先前得出的结论是相反的，但需要注意的是这组实验若参照上一组的结论（多个小卷积核的堆叠比有同样感受野规模的大卷积性能好）可以发现感受野不同因而没有可比性。但因层数相同（也是非线性变化相同），我们可以勉强得到另一个初步结论：层数（非线性变换）相同下，小卷积核性能不如大卷积核。因为其他有关卷积的超参数存在，还需要进一步做更多的实验来验证这个结论。最后再一次非常感谢Ant同学！

4.2 多尺度评估

也就是对输入图像在一定范围内的随机尺度缩放，模型最终的结果，是基于不同尺度（赌赢多个不同值的Q）且是crop后的图像跑网络得到的softmax结果的平均。

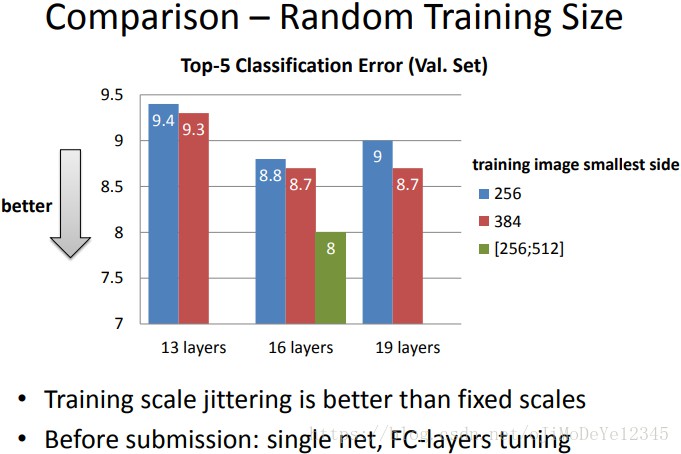
用固定大小的尺度S训练的模型，用三种尺寸Q去评估，其中$Q=[S – 32, S, S + 32]$ ；
用尺度S随机的方式训练模型，$S \in [S_{min}; S_{max}]$，评估使用更大的尺寸范围$Q=\{S_{min}, 0.5(S_{min}+S_{max}), S_{max}\}$。

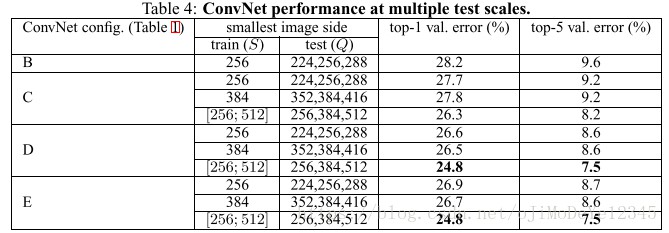
多尺度评估结果如上表所示，C、D、E这三组有随机尺度训练，发现效果比固定尺度训练的模型带来的性能更好。但我认为也很有可能是尺寸大带来的结果，之前我在跑120类狗分类数据集时，尺寸设置224和512分别训练，训练集和验证集的准确率基本收敛时，分辨率224×224的top1
accuracy 在30%左右，而分辨率512×512的top1 accuracy在50%~60%。所以我觉得这个实验不够说明随机 scale 带来的性能优势，因为固定尺寸的最大尺寸（384）比随机尺寸的最大尺寸（512）要小很多。当然，仍旧是深度随着递增越来越深（C、D、E，也要考虑宽度）的网络性能越好。

4.3 多crop评估

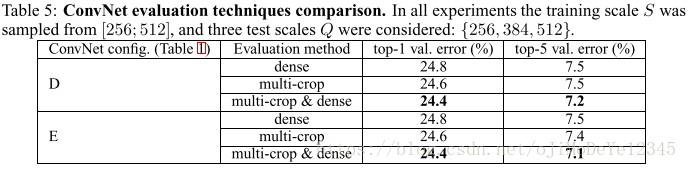
作者比较了dense ConvNet evaluation 和 multi-crop evaluation。发现multi-crop比dense ConvNet 的 evaluation 性能稍好，二者通过 averaging softmax output 结合起来使用效果比二者之一要好。作者得到这样的结论有假定，这句话：

As noted above, we hypothesize that this is due to a different treatment of convolution boundary conditions.

没看懂这里的 convolution boundary conditions 是指什么，另外，关于dense crop/application/evaluation，这是在OverFeat有讲到的、偏工程刷比赛的做法，没什么实质性意义，经常刷比赛的同学可以去查查 OverFeat 中的 dense evaluation。

4.4 卷积网络融合（ConvNet Fusion）

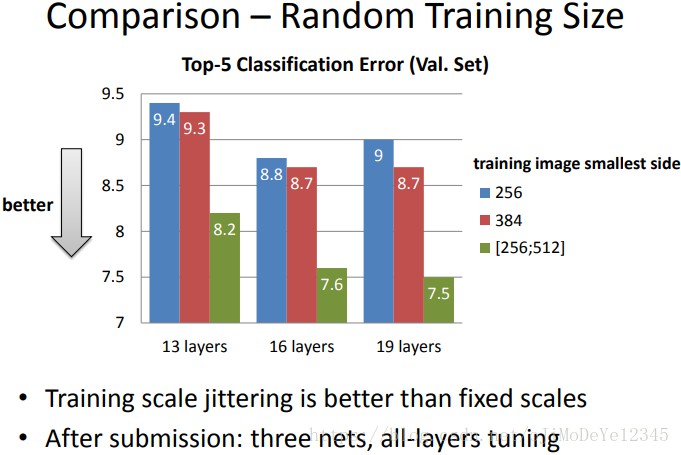
多模型融合是基于多个网络softmax输出的结果的平均，该方法在AlexNet和OverFeat中也有用到。

融合多卷积网络前，作者单尺度或者多尺度训练了模型，七个模型ensemble后的性能可以达到7.3%的top-5 error。最终作者选出两个最好的多尺度模型（D、E）融合，并使用dense和multi-crop的evaluation，top-5 error降到7.0%。最好的单模型是E，top-5 error为7.1%。

4.5 与其他SOTA模型比较

与其他state of the art的模型比较来看，单模型里最好的还是VGG，比GoogLeNet最好的单模型也要少0.9%的top-5 error。作者认为自己只是继承了1989年LeNet的卷积架构的基础上，主要就是加深了深度带来如此性能提升，当然我觉得这样说不合理，前面已经说过了，略。

5. Localization

作者在结论部分就是说模型在其他数据及上的性能也不错，另外就是深度matters。好了不说这些了，下面看看VGGNet是如何做到Localization第一的。

首先说一下localization，这是object detection的一种特例：

It can be seen as a special case of object detection, where a single object bounding box should be predicted for each of the top-5 classes, irrespective of the actual number of objects of the class.

预测出一个物体边界框，框需要给出top-5类别的每个边界框，而无需关注具体类别。在这里，作者采用的方法和2014年OverFeat（Sermanet et al获得ILSVRC-2013的localisation冠军）所使用的方法基本一致，略有修改。

物体定位也是使用卷积网络来实现，只是把最后原本分类的类别分数预测换成检测框的位置坐标预测。预测的检测框是一个4-D的向量，存储了中心点的坐标以及该检测框的宽度和高度，总共4个值。此外，对检测框预测的类别数也可以进行选择，这样就会有两种：

单类回归（single-class regression，SCR），OverFeat作者提出；
每类回归（class-specific regression，也就是per-class regression，PCR）。

第一种单类回归，最后的预测输出是4-D，而第二种最后的预测输出因为数据包含了1000个类别，所以是4000-D。作者使用在分类任务中表现最好的16层的VGG（D网络）来做这个任务。

5.1 训练

与前文所述的分类训练基本相同，主要不同在于将分类的逻辑斯特回归的目标函数换成了欧氏距离损失（Euclidean loss）：
$\frac 1 {2N} \sum_{i=1}^N | x^1_i – x^2_i |_2^2$

Header: ./include/caffe/layers/euclidean_loss_layer.hpp
CPU implementation: ./src/caffe/layers/euclidean_loss_layer.cpp
CUDA GPU implementation: ./src/caffe/layers/euclidean_loss_layer.cu

上面是来自caffe文档的欧氏距离损失，可以看一下cpu的实现：

template
void EuclideanLossLayer::Forward_cpu(const vector<Blob*>& bottom,
const vector<Blob*>& top) {
int count = bottom[0]->count();
caffe_sub(
count,
bottom[0]->cpu_data(),
bottom[1]->cpu_data(),
diff_.mutable_cpu_data());
Dtype dot = caffe_cpu_dot(count, diff_.cpu_data(), diff_.cpu_data());
Dtype loss = dot / bottom[0]->num() / Dtype(2);
top[0]->mutable_cpu_data()[0] = loss;
}

用caffe_sub来实现预测值和真实值相减，再用caffe_cpu_dot实现差值的平方最后把结果保存在dot变量里，并除以2N后将loss保存。

作者训练了两个不同尺度S的模型：S=256、S=384。因为ImageNet比赛 deadline缘故，没有做训练图像的尺度随机（scale jittering）resize的 augmentation。训练初始化是用对应的分类模型（同样尺度规模），初始学习率为0.001。作者尝试了fine-tune所有层以及前两个全连接层两种，OverFeat也曾使用过的方法。最后一个全连接层随机初始化并从头训练。作者正文写的是VGG用于分类的描述，这里区别是将最后一个SoftMax层（SoftMax就是逻辑斯特回归的更一般形式，虽名为回归，但实际一般是用于分类问题，“逻辑”我的理解是最后的值映射范围在零与一之间的小数，即逻辑值。上图的Sigmoid即S型函数，也是逻辑回归函数的形式，这一形式包括Tanh也是传统的激活函数的形式）换成欧氏距离等可以衡量距离的损失/目标函数的形式。

这里检测框的信息是通过欧氏距离度量来计算误差，得到损失函数并去优化，进行参数更新迭代。除了欧氏距离，其他关于距离度量的函数还有曼哈顿距离、切比雪夫距离、闵可夫斯基距离、标准化欧氏距离、马氏距离、汉明距离、杰卡德距离&杰卡德相似系数，当然还可以用相关系数&相关距离来计算，另外我查到还有信息熵也可以用于相似性度量，那么我想用于决策树特征分叉的基尼系数也是可以的咯！关于更多有关度量学习，可以参考这个CMU的Liu Yang做的Matlab工具箱DistLearnKit和其综述：

A Matlab Toolkit for Distance Metric Learning
http://www.cs.cmu.edu/~liuy/distlearn.htm

5.2 测试

作者使用两种测试方法：

crop resize 到Q尺度的图像的中间区域，然后喂给网络回归出4-D的检测框结果；
对全图使用 localisation 的卷积网络做dense evaluation。与分类任务类似，不同在于将最后一个用于产生类别分数特征的全连接层换成检测框预测的特征。拿到最后的检测框预测是通过贪心合并的过程（Sermanet等人2014年的OverFeat），该过程会首先通过平均某些坐标值来合并时空接近的预测，之后再基于卷积网络算出的类别分数来排序。当使用多个localisation网络，我们先把所有预测出的检测框结果进行贪心合并过程（和刚刚说的方法一样，通过平均坐标来合并空间临近的预测结果）。作者没有使用OverFeat所使用的 Multiple pooling offsets technique，该方法类似非最大值抑制，可以增加预测出来的检测框的spatial resolution和结果性能，没理解这里说的spatial resolution是什么，感觉像是空间辨识能力，毕竟该方法和最大值抑制，应该是筛掉一些结果，使得预测的检测框更具突出（差异性，或许也就是作者所说的spatial resolution）。

5.3 Localization实验

作者使用第一种测试评估的方法确定 Localization 的设定，我的理解是某些超参数的设定。之后再次使用第二种测试评估方法，即 fully-fledged。定位的误差是根据ILSVRC标准确定的（Russakovsky等人2014），例如预测的检测框与ground-truth检测框的IOU（intersection-over-union）大于0.5就视为预测正确。

5.3.1 参数设定

因为有在测试时根据预测的类别数，分为两种测试方法：第一种单类回归（SCR），最后的预测输出是4-D，而第二种每类回归（PCR），最后的预测输出包含了1000个类别即4000-D。作者比较发现单类回归效果比多类要好，这和OverFeat实验得出的结论相反。

其实我的理解更倾向于OverFeat 的结论：单类回归（PCR）比每类回归（SCR）结果好。是可能单类回归（SCR）的效果更好，我认为单类相比每类回归，无论是模型参数的分布抑或学习目标都是基于4-D的，学习压力会小许多，而让模型一次考虑太多如1000类，反而可能在考虑太多类的情况下去平衡每个类，网络学到的参数可能并不好。当然，因为我并没做实验，只是根据RCNN中用SVM来分类而不是SoftMax这一个点的感性的理解，RCNN认为用 SVM 相比 SoftMax 的优势在于：1. 收敛快（跑1个epoch后，SVM基本就收敛）；2. 效果好（比SoftMax好，这也是最主要的）。

此外，作者还发现 fine-tune 所有层后的性能要比仅 fine-tune 全连接层拿到的结果好。这是对于作者用CNN做Localization来说的（其它分类任务时，CNN只是用来提取特征，用SVM来做分类）。

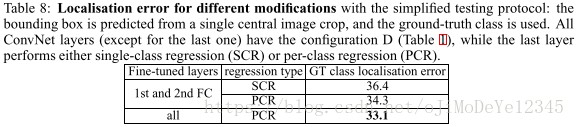
上图是作者根据下面的参数设定得到的性能结果，比较流程如下：

比较单类回归（SCR）和每类回归（PCR）的性能。发现每类回归效果好；
对比在 Localization 任务中，fine-tune所有层比仅fine-tune全连接层拿到的模型性能好（这点和OverFeat得出的结论一样）；
图像的训练尺寸。这点其实和选择的 pre-trained 模型有关，作者发现最短边S=384或者256性能差不多（the result with S=256 exhibit the same behavior and are not shown for brevity）。但仍然选择的是S=384的pre-trained模型；
全面评估（fully-fledged evaluation）。和正文里分类时类似， Localization 用了densely-computed bounding box预测，同时将预测得比较临近的检测框使用 OverFeat 的方法进行检测框的合并。同时作者发现，用整幅图比用图中心的 crop 来回归，得出的性能好，此外作者还使用了不同的scale去测试，而且还通过结合多个网络的预测结果，得到了更好的性能。

5.3.2 与其他SOTA比较

作者拿到2014年 localization 问题的第一名，相比前一年的冠军OverFeat，VGG用了更少的scale并且没有使用分辨率增强技术（resolution enhancement technique）。当然作者也认为如果用上了这样的技术，VGG模型的性能会更好，又再一次强调了模型深度带来更好的localization性能，尽管是一个比较简单的localization方法，但特征的表达非常卓越。其实说白了，还是看特征提取的好不好，所以我想，总结出来那就是：性能不好、特征不够，变换多尺度多模型来凑。

6. 评价

最后贴出CS231n的评价：

The runner-up in ILSVRC 2014 was the network from Karen Simonyan and Andrew Zisserman that became known as the VGGNet. Its main contribution was in showing that the depth of the network is a critical component for good performance. Their final best network contains 16 CONV/FC layers and, appealingly, features an extremely homogeneous architecture that only performs 3×3 convolutions and 2×2 pooling from the beginning to the end. Their pretrained model is available for plug and play use in Caffe. A downside of the VGGNet is that it is more expensive to evaluate and uses a lot more memory and parameters (140M). Most of these parameters are in the first fully connected layer, and it was since found that these FC layers can be removed with no performance downgrade, significantly reducing the number of necessary parameters.

我这里对其简单总结下：

深度提升性能；
最佳模型：VGG16，从头到尾只有3×3卷积与2×2池化。简洁优美；
开源pretrained model。与开源深度学习框架Caffe结合使用，助力更多人来学习；
卷积可代替全连接。整体参数达1亿4千万，主要在于第一个全连接层，用卷积来代替后，参数量下降（这里的说法我认为是错的，替代前后用同样的输入尺寸，网络参数量、feature map、计算量三者没有变化）且无精度损失。

参考

以下是一些参考文献，虽然不少地方引用了，但是偷懒没有在文中具体标明。老实说，有时间能看原汁原味的东西就不要看别人吃过的，即使我写的这篇，看原版的东西我觉得收获更大一些。

Last modification：January 6th, 2021 at 10:34 am

暂无相关推荐

论文理解 - VGGNet - Very Deep Convolutional Networks for Large-Scale Image Recognition[转]

AIHGF • 2018 年 05 月 22 日

原文 - Very deep convolutional networks for large-scale image recognition
论文: Very Deep Convolutional Networks for Large-Scale Image Recognition
一篇对 VGGNet 理解比较详细的博客，很长很详尽，十分受用.
转载并非常感谢原博主 - Yuens's Blog.

GoogLeNet和VGG的Classification模型从原理上并没有与传统的CNN模型有太大不同。大家所用的Pipeline也都是：训练时候：各种数据Augmentation（剪裁，不同大小，调亮度，饱和度，对比度，偏色），剪裁送入CNN模型，Softmax，Backprop。测试时候：尽量把测试数据又各种Augmenting（剪裁，不同大小），把测试数据各种Augmenting后在训练的不同模型上的结果再继续Averaging出最后的结果.
参考：如何评价今年的 ILSVRC 2014 结果？ | 知乎
https://www.zhihu.com/question/24904450/answer/29400634

继承了AlexNet不少网络结构（基于它加深层数和修改所有卷积核为3×3的小卷积），最后三个fc层基本算是平移AlexNet的到VGGNet上；
继承了OverFeat在Localization任务中的做法（we adopt the approach of Sermanet et al. (2014)，没记错的话OverFeat拿了2013年Localization任务的第一名.）

这篇文章的主要特别的地方是前两点（换句话说，抄的不是很明显）：

卷积核变小。作者做的6组实验中，卷积核全部替换为3×3（极少用了1×1），选用更小卷积核的motivation是作者受到这两篇文章（Zeiler & Fergus, 2013; Sermanet et al., 2014）启发，使用更小的卷积核尺寸和stride得到性能提升；
层数更深更宽（11层、13层、16层、19层）。我认为作者是觉得：既然小卷积核带来性能提升，那么不妨试试深度对性能的影响，反正参数量我的gpu可以cover住。作者的实验也发现层数越深，带来的分类结果也越好，但并没有提到channel变宽这一个因素：6组实验中channel数都是逐层加宽的，如果单说深度对性能的影响而忽略宽度（这里宽度不是feature map的width而是depth），我觉得并不够convincing，应该再加入一下对宽度（channel）数分析对比的实验；
池化核变小且为偶数。AlexNet中的max-pool全是3×3的，但VGGNet中都是2×2的。作者没有说明选择这种size的考量（现在stride=2、以及2×2和3×3的pooling kernel选择的主流），我认为主要是2×2带来的信息损失相比3×3的比较小，相比3×3更容易捕获细小的特征变化起伏，此外或许是发现2×2的实验效果确实比3×3的好吧（毕竟这也是直接原因）；
网络测试阶段将训练阶段的三个全连接替换为三个卷积。对于训练和测试一样的输入维度下，网络参数量没有变化，计算量也没有变化，思想来自OverFeat，1×1的卷积思想则来自NIN。优点在于全卷积网络可以接收任意尺度的输入（这个任意也是有前提的，长和宽都要满足：$a\times2^n$，n是卷积与池化做stride=2的下采样的次数）；
刷比赛的小技巧。其实没什么意思，比方输入图片的尺寸对于训练和测试阶段的处理方式不同，single和multi-scale的问题（具体见后文）。

下面我将会任务背景开始说明，最后我会再次引用CS231n对于VGG的中肯评价进行总结。

1. 任务背景

小卷积核。在第一个卷积层用了更小的卷积核和卷积stride（Zeiler & Fergus, 2013; Sermanet et al., 2014）；
多尺度。训练和测试使用整张图的不同尺度（Sermanet et al., 2014; Howard, 2014）。

1.1 优秀的特征提取器和泛化能力

1.1.1 特征提取器

（Supervised pre-training）用12年的分类数据去pre-train模型，CNN后接1k-way softmax
（Domain-specific fine-tuning）用当年20类检测数据集生成分类数据（根据检测数据通过selective search生成小图，然后计算IOU大于0.5视为该类图像），去fine-tune模型，CNN后接20-way softmax；
（Object category classifier）CNN参数固定，训练SVM。输入SVM的数据是CNN处理后的feature map，如果是20类那么对应20个，即分类20类的二分类SVM。其中对于某一类的SVM来说，正样本是proposal和ground-truth的框IOU大于0.3的（交叉验证得到的），其余视为负样本；
（Bounding-box regression）这里原图没有画出，其实在检测这里既有对proposal进行分类，再有对proposal的中心点和宽和高这四个值进行回归的过程，当然这个regressor的参数是训练拿到的。

数据量小的新任务。可以把前面的大部分层参数freeze，保留前面的卷积层和部分卷积层，以获取在ImageNet上得到的提取特征的能力，作为特征提取器，而只训练最后一层的全连接层。
数据量中等的新任务。则需要更多的可变的层来拟合新任务的数据，freeze前面的层，留出更多的层去拟合新数据。

不过可以发现，无论网络深浅，最后一层（或几层）总是对应类别的轮廓，即语义信息。

1.1.2 在其它数据集上的泛化性

一开始在量级大且多样性广的数据集（如ImageNet）上pre-train，不严谨地说，新问题的小数据只是当初pre-train时所用数据集的一个子集，换句话说，pre-trained模型的参数已经避开了用小数据train-from-scratch的一些局部最优；
一开始在足够大的数据上pre-train，模型已经见识过了广阔的样本空间，这会带来了更广阔和丰富的特征空间，因而模型在小数据上学习时不会太过纠结于比较片面或者偏斜的样本带来的影响（还是类似第一点，初始化足够好）。

$$ x’_{i,j} = \frac{x_{i,j}}{\sqrt{ \sum_{i=0}^{height-1} \sum_{j=0}^{width-1} x_{i,j}^2 }} $$

2. ConvNet Configurations

为了方便分析，先把VGGNet16的结构图放出来，即将说到的内容会跟下面这幅图有很密切的关系：

结合这张图，我们有网络D的参数表格（参数来自CS231n的计算，我这里重新排版）：

参数太少。像relu、pool这样的层参数量太少，有的甚至如激活层relu不保存中间结果直接给下一层；
计算量小。相比conv甚至fc，pool这些层的计算量太少。

2.1 卷积

但似乎这里的公式写错了，应该写成：
$f[x,y] \ast g[x,y] = \sum_{n_1=-\infty }^{\infty} \sum_{n_2=-\infty }^{\infty} f[n_1,n_2] \cdot g[n_1-x, n_2-y]$

在知乎的“如何通俗的理解卷积？”这个问题下，找到一个比贾扬清的回答更易于理解的一个回答，下面是该回答中的计算过程示意图：

但需要注意的是，input matrix通常都是带有深度，或者说是厚度的（depth/channel），这个动态地在不同位置处卷积的过程也可用下图表示：

既然知道了卷积的做法，那么下面我将分析：

卷积核尺寸；
feature map的维度变化（height，width，depth）；
卷积组（相比AlexNet的变化及个人没有实验的感性分析）。

2.1.1 卷积核尺寸

说VGGNet的kernel size前，不妨先来看看AlexNet的kernel size，AlexNet的结构如下：

input=8，3层conv3x3后，output=2，等同于1层conv7x7的结果；
input=8，2层conv3x3后，output=2，等同于2层conv5x5的结果。

上图是用2个stride=1、padding=0的conv3x3来代替1个stride=2的conv5x5的例子。此外，作者在3个conv3x3代替1个conv7x7的做法上，认为有以下三点优势：

3个激活函数（ReLU）去代替1个，可使决策函数更加具有辨别能力，此外就卷积本身的作用而言，3×3 比 7×7 就足以捕获特征的变化：3×3的9个格子，最中间的格子是一个感受野中心，可以捕获上下左右以及斜对角的特征变化。主要在于3个堆叠起来后，三个3×3近似一个7×7，网络深了两层且多出了两个非线性ReLU函数，（特征多样性和参数参数量的增大）使得网络容量更大（关于model capacity，AlexNet的作者认为可以用模型的深度和宽度来控制capacity），对于不同类别的区分能力更强（此外，从模型压缩角度也是要摒弃7×7，用更少的参数获得更深更宽的网络，也一定程度代表着模型容量，后人也认为更深更宽比矮胖的网络好）；

以下是个人的深层思考：网络更深带来了更多变化，更好的特征多样性，就好比是数据增强虽然引来方差是好的，我们想在变化中寻找不变的映射关系。但是，网络更深带来特征更多真的好嘛？我觉得更多的特征和更深的网络，不一定都是有助于、有贡献于正确梯度下降寻找最优或者局部最优的方向，我们真正需要的是可以正确建立映射关系的特征。
反倒是层数越深，特征更多，会有更多局部最优。但为此，我们又在减少因引入特征多样性带来的高方差的影响，不论是在随机梯度下降中引入动量，还是各种正则化的手段，又尝试减少更深网络带来更多特征造成的影响。一方面我们在增大方差，又在减少方差。这样看，似乎这是矛盾的。
网络由于有着本身的更新策略，可以正确建立映射关系。但网络更深却在影响映射关系的建立，把这个建立的过程变得更加曲折，甚至无法建立出好的、正确的、有效的映射关系。
我想了想，感觉这是一个平衡，重要是多了可以筛选：
一方面，我们希望有更多特征，在于我们可以筛选。本身的更新策略可以指导映射关系的建立。但是学习的东西多了，必然会造成学习出现问题，因为要在其中筛选。但是所有的基于部分样本的优化带来的梯度估计，必然会学出的权重都有一点不正确。
另一方面，我们又在减少影响，减少不正确性带来的影响，就有这些正则化来去筛选。有的正则化起到筛选的作用，而有的则是减缓、减小高方差带来错误下降方向的影响的作用。
我觉得重点在于这个特征筛选做的好不好，现在大多情况都不缺数据。其实这样看来，即使是深度学习，又回到了以前的问题，特征工程、特征选择。似乎深度学习带来了更深的网络，表面上看给我们造成没有必要做特征工程的假象，但其实我们做了这个过程，在网络结构设计、模块选择、网络的训练（优化）trick里。
无论是特征跨 depth 的 cross（resnet），还是跨channel的cross（lrn、shufflenet）。这几年的网络都是在网络更dense的前提（比方mobilenet）下，基于各自的module做特征工程，引入更多特征，一方面特征 diverse 方差加大，一方面又用正则等手段钝化平滑方差。我认为，大家认为深度学习玄学的一个原因可能是不可估量的方差的 tradeoff 造成的。
有小伙伴也提到，玄学也是因为现在的文章中说到的方法其实并不是work的，你按照他说的这么调整就是不对。

conv filter的参数减少。相比5×5、7×7和11×11的大卷积核，3×3明显地减少了参数量。作者还使用了1×1的卷积核，认为1×1卷积核是channel级别的线性变换（毕竟一组channel用对应的一样的卷积核在这一组channel上扫描，一组channel不是指这一层feature map的所有channel）。比方input channel数和output channel数均为C，那么3层conv3x3卷积所需要的卷积层参数是：3x(Cx3x3xC)=27C^2 ，而一层conv7x7卷积所需要的卷积层参数是：Cx7x7xC=49C^2。conv7x7的卷积核参数比conv3x3多了(49-27)/27×100% ≈ 81%；
小卷积核代替大卷积核有正则作用。作者用三个conv3x3代替一个 conv7x7，认为可以进一步分解（decomposition）原本用7×7大卷积核提到的特征.

This can be seen as imposing a regularisation on the 7 × 7 conv. ﬁlters,
forcing them to have a decomposition through the 3 × 3 ﬁlters (with
non-linearity injected in between).

我没看明白，关于正则化在《Deep Learning》这本书的Chapter 7 Regularization for Deep Learning中是这么定义的：

In section 5.2.2, we deﬁned regularization as “any modiﬁcation we make
to a learning algorithm that is intended to reduce its generalization
error but not its training error.”

此外，搜了些相关资料，简单总结下1×1卷积的特点（就不说加入非线性这个conv自带的特点了）：

专注于跨通道的特征组合：conv1x1 根本不考虑单通道上像素的局部信息（不考虑局部信息），专注于那一个卷积核内部通道的信息整合。conv3x3 既考虑跨通道，也考虑局部信息整合；
对 feature map 的channel级别降维或升维：例如224x224x100的图像（或feature map）经过20个conv1x1的卷积核，得到 224x224x20 的 feature map。尤其当卷积核（即filter）数量达到上百个时，3×3 或 5×5 卷积的计算会非常耗时，所以 1×1 卷积在 3×3 或 5×5 卷积计算前先降低 feature map 的维度。

然而，分类性能上同样的单模型，VGGNet比GoogLeNet在top5的错分率要低，而多模型下，同样七个网络的VGGNet不如GoogLeNet。

2.1.2 feature map的维度变化

2.1.3 卷积组

前两组卷积形式一样，每组都是：conv-relu-conv-relu-pool；
中间三组卷积形式一样，每组都是：conv-relu-conv-relu-conv-relu-pool；
最后三个组全连接fc层，前两组fc，每组都是：fc-relu-dropout；最后一个fc仅有fc。

多出的relu对网络中层进一步压榨提炼特征。结合一开始单张 feature map 的 local 信息更多一些，还没来得及把信息分摊到 channel 级别上，那么往后就慢慢以增大 conv filter 的形式递增地扩大channel数，等到了网络的中层，channel数升得差不多了（信息分摊到channel上得差不多了），那么还想抽 local 的信息，就通过再加一个[conv-relu]的形式去压榨提炼特征。有点类似传统特征工程中，已有的特征在固定的模型下没有性能提升了，那就用更多的非线性变换对已有的特征去做变换，产生更多的特征的意味；
多出的conv对网络中层进一步进行学习指导和控制不要将特征信息漂移到channel级别上。
1. 上一点更多的是relu的带来的理解，那么多出的[conv-relu]中 conv 的意味就是模型更强的对数据分布学习过程的约束力/控制力，做到信息backprop可以回传回来的学习指导。本身多了relu特征变换就加剧（权力释放），那么再用一个 conv 去控制（权力回收），也在指导网络中层的收敛；
2. 其实 conv 本身关注单张feature map上的局部信息，也是在尝试去尽量平衡已经失衡的channel 级别（depth）和local级别（width、height）之间的天平。这个conv控制着特征的信息量不要过于向着channel级别偏移。

关于卷积组（Layer pattern），CS231n的博客给出如下观点：

串联和串联中带有并联的网络架构。近年来，GoogLeNet在其网络结构中引入了Inception模块，ResNet中引入了Residual Block，这些模块都有自己复杂的操作，上图就是Inception模块。换句话说，传统一味地去串联网络可能并不如这样串联为主线，带有一些并联同类操作但不同参数的模块可能在特征提取上更好。
所以我认为这里本质上依旧是在做特征工程，只不过把这个过程放在里 block 或者 module 的小的网络结构里，毕竟 kernel、stride、output 的大小等等超参数都要自己设置，目的还是产生更多丰富多样的特征。
用在 ImageNet 上 pre-trained 过的模型。设计自己模型架构很浪费时间，尤其是不同的模型架构需要跑数据来验证性能，所以不妨使用别人在 ImageNet 上训练好的模型，然后在自己的数据和问题上在进行参数微调，收敛快精度更好。
我认为只要性能好精度高，选择什么样的模型架构都可以，但是有时候要结合应用场景，对实时性能速度有要求的，可能需要多小网络，或者分级小网络，或者级联的模型，或者做大网络的知识蒸馏得到小网络，甚至对速度高精度不要求很高的，可以用传统方法。

2.1.4 Layer Sizing Patterns

要说到layer pattern，不得不提到 sizing pattern，这也是CS231n里所讲到的。对于每种层，有不同的默认设定：

输入层：大都是 2 的N次方，这和网络中卷积或者池化层出现的 stride 为 2 的次数有关，比方VGGNet中每个 pattern 的卷积不会对 feature map 的宽度和高度有改变，而每个pattern结束前总会做一个 stride 为 2 的下采样，因为有 5 组，那么做 5 次就是 32，所以VGGNet网络input大小一般都是 32 的倍数，即 $a \times 2^n$，$n$ 是下采样的次数，$a$ 是最终卷积和池化得到的feature map大小，如224或者384。

其实对于边界问题的处理，主要有4种方法：

用0填充，相当于黑色，卷积核对应位置相乘也是0；
用边界的邻近像素扩展；
把图当做一个循环，同一行最右边的填补使用最左边的像素；
舍弃无法卷积的部分。

卷积层：现在常用的是小卷积核如 3×3 或者 1×1。卷积为了保留feature map不变，通常会采取 pad 为 1 的操作，其实具体来说应该是：为了保证卷积后的 feature map的宽度和高度不变，那么有 $pad=(F-1)/2$，但我觉得这个有点问题，可以改成更一般的形式，不过首先可以看看计算下一层feature map宽高的公式：
$W_2 = (W_1 – F + 2P) / S + 1$

池化层：常见2×2的max-pooling，少见3×3或者更大的kernel。更大的kernel带来的问题是信息丢失带来的信息损失，此外，stride通常为2；其实按照以上的设定看来，也是有好处的。卷积专注于保留空间信息前提下的channel变换，而池化则专注于空间信息的变换（下采样）.

2.2 池化

VGGNet 中的 max-pool 均采用kernel为2×2的尺寸，stride为2的设定。这里和AlexNet有区别，AlexNet使用的max-pool的kernel为3×3大小，stride为2的pool。

max：反向过程会记录当时正向时最大值的位置，反向则最大值位置不变，其他位置填补0；
average：反向过程会将正向的平均值，以平均的形式分摊到每个位置；
stochastic：反向一样记录正向时时被随机选中的位置，该位置值不变，其他位置填补0。

2.3 全连接

形式上完全平移AlexNet的最后三层，VGGNet后面三层（三个全连接层）为：

FC4096-ReLU6-Drop0.5，FC为高斯分布初始化（std=0.005），bias常数初始化（0.1）
FC4096-ReLU7-Drop0.5，FC为高斯分布初始化（std=0.005），bias常数初始化（0.1）
FC1000（最后接SoftMax1000分类），FC为高斯分布初始化（std=0.005），bias常数初始化（0.1）

2.4 其它

3. 训练和测试

3.1 训练阶段

除了对训练图像的多尺度后的crop进行采样训练，其它和AlexNet基本一致：

优化方法：带动量（momentum）的小批量梯度下降
batch size：256
learning rate：0.01
和AlexNet一样，当val-acc 不下降则学习率缩小十倍，训练过程缩小了三次
momentum：0.9
weight decay（$L_2$惩罚乘子）：$5 \times 10^{-4}$
dropout rate（前两个全连接层）：0.5
目标函数：多项式逻辑斯特回归（SoftMax）
迭代次数：37万次iteration（74 epochs）后，停止训练

尽管模型参数量是AlexNet的3倍多且层数深，但跑的epochs比AlexNet少收敛快，作者认为是以下两点原因：

正则化：dropout和小卷积核的使用。关于dropout，我记得AlexNet有写道：前两个全连接层用到了dropout，若没有dropout模型必然会过拟合，但是有dropout后，收敛大约需要原本两倍的 iteration 次数。我对 dropout 的理解是模型 ensemble，每次iteration对原网络dropout 一些神经元后的模型可视为一个单独的模型，最后test时则是ensemble的模型，效果必然好于单模型。参数越多越容易过拟合，比方全连接层比卷积层要容易过拟合，全连接层因为参数量大，好比一个多元高次函数，而卷积层好比简单的函数，多元高次的函数肯定在捕捉细节特征上会比简单函数好，但代价就是训练时间更长，需要正则化等方法去平衡。对于收敛更快，我认为主要是小卷积核带来的优势，小卷积核参数少，从训练样本中需要拟合/学习的参数自然少，而且backprop的时候涉及到前面的范围也比较小，因而似乎会收敛快（但我不认为这是 VGG 比 AlexNet 收敛快的根本原因）；
pre-initialisation，相当于预训练。为了防止不好的初始化会导致训练过程中停止学习，作者把A实验的模型的前四个卷积层和三个全连接层的参数拿来作为模型的初始化参数，中间层的初始值从均值为0，方差为0.01的正态分布中采样得到，bias初始化为0，学习率设定和训练A（相当于pre-train）时的一样。虽然作者没有承认pre-initialisation是预训练，但本质上就是。好处主要两点：性能比train-from-scratch有提高，且收敛更。

其实我想说，收敛更快的主要原因很可能就是预训练，说小卷积核和dropout有点扯，感觉正则只会延长训练过程。另外在知乎看到一个观点很有意思：

便也要纠正一下在提到CNN的时候经常出现的错误：“CNN的参数太多，造成学习困难。”
其实CNN相比较于以前的模型，参数并不见得多：在CNN之前，NEC Labs 采用 sparse SIFT＋Pyramid Pooling的方法取得过ILSVRC的冠军，在这些模型中，最后线性SVM的输入特征在160K 到 260K不等。因为一共有1000类，所以SVM的总参数是160M－260M左右。Alex 2012年的模型只有60M参数，而我们今年的模型大概只有7M。（补充编辑：这些图像特征一般都是稀疏的，但是SVM的参数并不稀疏。）
所以，其实我们应该说的是，CNN的优化是一个非凸（non-convex）的问题，所以才比较困难.
参考：如何评价今年的 ILSVRC 2014 结果？
https://www.zhihu.com/question/24904450

3.1.1 训练图像尺寸

作者使用两种方法设置训练图像的尺度S：

固定训练图像的最短边S，用这种单一尺度去训练。即使是短边固定了，但依然对原图 crop 得到多种尺度的信息。作者使用S=256（借鉴AlexNet等人）和S=384。作者先用 S=256 crop出的图像去训练网络，之后再用 S=384 crop出的图像去fine-tune网络（该过程用了比S=256时更小的学习率0.001）；
多种短边尺度S训练。给定S的一个范围，作者使用[256, 512]。这样带来的好处是需要分类或者 localize 的物体本身在图像上的像素就不同，这样在训练中就把这一因素考虑进去。这也可以看做是 data augmentation 里的尺度扩增（scale jittering），这样训练同一个模型时是基于不同尺度的图像进行的。作者依然是为了speed reason（太假了，明显是因为fine-tine效果好，还不承认），基于model A 去 fine-tune了所有层。但是pre-train mode是采用固定尺寸384的最短边的训练图像crop出的224的图，去train-from-scratch的.

3.2 测试阶段

3.2.1 全连接转为卷积

下面这段来自作者原文test小节的具体流程：

At test time, given a trained ConvNet and an input image, it is classified in the following way.
First, it is isotropically rescaled to a pre-defined smallest image side, denoted as Q (we also refer to it as the test scale). We note that Q is not necessarily equal to the training scale S (as we will show in Sect. 4, using several values of Q for each S leads to improved performance).
Then, the network is applied densely over the rescaled test image in a way similar to (Sermanet et al., 2014). Namely, the fully-connected layers are first converted to convolutional layers (the first FC layer to a 7 × 7 conv. layer, the last two FC layers to 1 × 1 conv. layers). The resulting fully-convolutional net is then applied to the whole (uncropped) image. The result is a class score map with the number of channels equal to the number of classes, and a variable spatial resolution, dependent on the input image size.
Finally, to obtain a fixed-size vector of class scores for the image, the class score map is spatially averaged (sum-pooled).
We also augment the test set by horizontal flipping of the images; the soft-max class posteriors of the original and flipped images are averaged to obtain the final scores for the image.

其中比较特别的一点在这句：

Namely, the fully-connected layers are first converted to convolutional layers (the first FC layer to a 7 × 7 conv. layer, the last two FC layers to 1 × 1 conv. layers).

此外，我有想到四个问题：

文中说对 class score 做 average，但并未说这个 class score 是在 softmax 前还是后得到的。具体而言，作者在这里没有具体说明是将6x6x1000的 feature map 先做average到 1x1x1000 的维度后再做 SoftMax，还是先给 SoftMax 分类，得到 6x6x1000 的结果，再对每个结果进行average？因为作者没有说清楚，不过我觉得两个都可以试试，看哪种效果好用哪个。后来我想到 softmax 前必须是1k维的，因为 softmax 只是一个 soft-max，具体可以看看softmax的公式，这一来如果是 6x6x1000 的 feature map 需要在 softmax 前做 average 到 1x1x1000 才行；
直接把训练阶段的全连接参数当做测试阶段的卷积参数，不需要做参数微调嘛？做和不做，哪个效果更好？不过我可以想来如果用同样数据，效果可能不好或者持平，但是解决不同的问题或许再做 fine-tune，效果说不定会更好；
有实验表明将最后所有FC层转为CONV后，比方 384x384x3 的图，最后得到 6x6x1000 的feature map 与不转换 fc 为 conv 的单个网络跑36次，效果会更好嘛？
单个网络模型下，同样或者不同尺寸的图输入到转换前和转换后的网络，全卷积网络的性能更好吗？

以上问题都需要做实验才能得出，最近懒得动，也就捂脸不多说了。

4. 分类实验

12年到14年的挑战赛都使用的是 1000 个类别的ILSVRC-2012数据集（Large Scale Visual Recognition Challenge），其中：

训练集：130万张图片；
验证集：5万张图片；
测试集：10万张图片，这组数据的label没有给出（with held-out class labels）。

4.1 单尺度评估

对每个网络（总共六个）进行单独评估，测试图像尺寸依训练时的尺寸设定分为两种情况：

训练图像的尺寸S固定时，设置训练图像尺寸S等于测试图像尺寸Q；
训练图像尺寸S是介于$[S_{min}, S_{max}]$时，设置测试图像尺寸$Q=0.5(S_{min}+S_{max})$。

实验结论：

LRN层无性能增益（A和A-LRN）。作者通过网络A和A-LRN发现AlexNet曾经用到的LRN层（local response normalization，LRN是一种跨通道去normalize像素值的方法）没有性能提升，因此在后面的4组网络中均没再出现LRN层。
当然我也感觉没啥用，想到 max-pooling 比 average-pooling 效果好，我就感觉这个LRN没啥用，不过如果把 LRN 改成跨通道的 max-normal，我感觉说不定会有性能提升。特征得到retain更明显。
深度增加，分类性能提高（A、B、C、D、E）。从11层的A到19层的E，网络深度增加对top1和top5的error下降很明显，所以作者得出这个结论，但其实除了深度外，其他几个网络宽度等因素也在变化，depth matters 的结论不够 convincing。
conv1x1的非线性变化有作用（C和D）。C和D网络层数相同，但D将C的3个conv3x3换成了conv1x1，性能提升。这点我理解是，跨通道的信息交换/融合，可以产生丰富的特征易于分类器学习。conv1x1相比conv3x3不会去学习local的局部像素信息，专注于跨通道的信息交换/融合，同时为后面全连接层（全连接层相当于global卷积）做准备，使之学习过程更自然。
多小卷积核比单大卷积核性能好（B）。作者做了实验用B和自己一个不在实验组里的较浅网络比较，较浅网络用conv5x5来代替B的两个conv3x3。多个小卷积核比单大卷积核效果好，换句话说当考虑卷积核大小时：depths matters。
非常非常感谢严谨的Ant同学，这里第四个结论的描述不够严谨及结论表述不清导致的这个错误。原文中说到：在同样感受野范围下，用5×5的卷积去等效替代3×3卷积的网络性能下降。因而我得出“多小卷积核比单大卷积核性能好”这一结论。这一结论我描述的不够严谨，应该改为：“多个小卷积核的堆叠比有同样感受野规模的大卷积性能好。”

4.2 多尺度评估

用固定大小的尺度S训练的模型，用三种尺寸Q去评估，其中$Q=[S – 32, S, S + 32]$ ；
用尺度S随机的方式训练模型，$S \in [S_{min}; S_{max}]$，评估使用更大的尺寸范围$Q=\{S_{min}, 0.5(S_{min}+S_{max}), S_{max}\}$。

4.3 多crop评估

As noted above, we hypothesize that this is due to a different treatment of convolution boundary conditions.

4.4 卷积网络融合（ConvNet Fusion）

多模型融合是基于多个网络softmax输出的结果的平均，该方法在AlexNet和OverFeat中也有用到。

4.5 与其他SOTA模型比较

5. Localization

作者在结论部分就是说模型在其他数据及上的性能也不错，另外就是深度matters。好了不说这些了，下面看看VGGNet是如何做到Localization第一的。

首先说一下localization，这是object detection的一种特例：

It can be seen as a special case of object detection, where a single object bounding box should be predicted for each of the top-5 classes, irrespective of the actual number of objects of the class.

单类回归（single-class regression，SCR），OverFeat作者提出；
每类回归（class-specific regression，也就是per-class regression，PCR）。

5.1 训练

Header: ./include/caffe/layers/euclidean_loss_layer.hpp
CPU implementation: ./src/caffe/layers/euclidean_loss_layer.cpp
CUDA GPU implementation: ./src/caffe/layers/euclidean_loss_layer.cu

上面是来自caffe文档的欧氏距离损失，可以看一下cpu的实现：

template
void EuclideanLossLayer::Forward_cpu(const vector<Blob*>& bottom,
const vector<Blob*>& top) {
int count = bottom[0]->count();
caffe_sub(
count,
bottom[0]->cpu_data(),
bottom[1]->cpu_data(),
diff_.mutable_cpu_data());
Dtype dot = caffe_cpu_dot(count, diff_.cpu_data(), diff_.cpu_data());
Dtype loss = dot / bottom[0]->num() / Dtype(2);
top[0]->mutable_cpu_data()[0] = loss;
}

用caffe_sub来实现预测值和真实值相减，再用caffe_cpu_dot实现差值的平方最后把结果保存在dot变量里，并除以2N后将loss保存。

A Matlab Toolkit for Distance Metric Learning
http://www.cs.cmu.edu/~liuy/distlearn.htm

5.2 测试

作者使用两种测试方法：

crop resize 到Q尺度的图像的中间区域，然后喂给网络回归出4-D的检测框结果；
对全图使用 localisation 的卷积网络做dense evaluation。与分类任务类似，不同在于将最后一个用于产生类别分数特征的全连接层换成检测框预测的特征。拿到最后的检测框预测是通过贪心合并的过程（Sermanet等人2014年的OverFeat），该过程会首先通过平均某些坐标值来合并时空接近的预测，之后再基于卷积网络算出的类别分数来排序。当使用多个localisation网络，我们先把所有预测出的检测框结果进行贪心合并过程（和刚刚说的方法一样，通过平均坐标来合并空间临近的预测结果）。作者没有使用OverFeat所使用的 Multiple pooling offsets technique，该方法类似非最大值抑制，可以增加预测出来的检测框的spatial resolution和结果性能，没理解这里说的spatial resolution是什么，感觉像是空间辨识能力，毕竟该方法和最大值抑制，应该是筛掉一些结果，使得预测的检测框更具突出（差异性，或许也就是作者所说的spatial resolution）。

5.3 Localization实验

5.3.1 参数设定

上图是作者根据下面的参数设定得到的性能结果，比较流程如下：

比较单类回归（SCR）和每类回归（PCR）的性能。发现每类回归效果好；
对比在 Localization 任务中，fine-tune所有层比仅fine-tune全连接层拿到的模型性能好（这点和OverFeat得出的结论一样）；
图像的训练尺寸。这点其实和选择的 pre-trained 模型有关，作者发现最短边S=384或者256性能差不多（the result with S=256 exhibit the same behavior and are not shown for brevity）。但仍然选择的是S=384的pre-trained模型；
全面评估（fully-fledged evaluation）。和正文里分类时类似， Localization 用了densely-computed bounding box预测，同时将预测得比较临近的检测框使用 OverFeat 的方法进行检测框的合并。同时作者发现，用整幅图比用图中心的 crop 来回归，得出的性能好，此外作者还使用了不同的scale去测试，而且还通过结合多个网络的预测结果，得到了更好的性能。

5.3.2 与其他SOTA比较

6. 评价

最后贴出CS231n的评价：

The runner-up in ILSVRC 2014 was the network from Karen Simonyan and Andrew Zisserman that became known as the VGGNet. Its main contribution was in showing that the depth of the network is a critical component for good performance. Their final best network contains 16 CONV/FC layers and, appealingly, features an extremely homogeneous architecture that only performs 3×3 convolutions and 2×2 pooling from the beginning to the end. Their pretrained model is available for plug and play use in Caffe. A downside of the VGGNet is that it is more expensive to evaluate and uses a lot more memory and parameters (140M). Most of these parameters are in the first fully connected layer, and it was since found that these FC layers can be removed with no performance downgrade, significantly reducing the number of necessary parameters.

我这里对其简单总结下：

深度提升性能；
最佳模型：VGG16，从头到尾只有3×3卷积与2×2池化。简洁优美；
开源pretrained model。与开源深度学习框架Caffe结合使用，助力更多人来学习；
卷积可代替全连接。整体参数达1亿4千万，主要在于第一个全连接层，用卷积来代替后，参数量下降（这里的说法我认为是错的，替代前后用同样的输入尺寸，网络参数量、feature map、计算量三者没有变化）且无精度损失。

1. 任务背景

1.1 优秀的特征提取器和泛化能力

1.1.1 特征提取器

1.1.2 在其它数据集上的泛化性

2. ConvNet Configurations

2.1 卷积

2.1.1 卷积核尺寸

2.1.2 feature map的维度变化

2.1.3 卷积组

2.1.4 Layer Sizing Patterns

2.2 池化

2.3 全连接

2.4 其它

3. 训练和测试

3.1 训练阶段

3.1.1 训练图像尺寸

3.2 测试阶段

3.2.1 全连接转为卷积

4. 分类实验

4.1 单尺度评估

4.2 多尺度评估

4.3 多crop评估

4.4 卷积网络融合（ConvNet Fusion）

4.5 与其他SOTA模型比较

5. Localization

5.1 训练

5.2 测试

5.3 Localization实验

5.3.1 参数设定

5.3.2 与其他SOTA比较

6. 评价

参考

※相关文章推荐※

※最新文章推荐※

Leave a Comment Cancel reply

论文理解 - VGGNet - Very Deep Convolutional Networks for Large-Scale Image Recognition[转]

1. 任务背景

1.1 优秀的特征提取器和泛化能力

1.1.1 特征提取器

1.1.2 在其它数据集上的泛化性

2. ConvNet Configurations

2.1 卷积

2.1.1 卷积核尺寸

2.1.2 feature map的维度变化

2.1.3 卷积组

2.1.4 Layer Sizing Patterns

2.2 池化

2.3 全连接

2.4 其它

3. 训练和测试

3.1 训练阶段

3.1.1 训练图像尺寸

3.2 测试阶段

3.2.1 全连接转为卷积

4. 分类实验

4.1 单尺度评估

4.2 多尺度评估

4.3 多crop评估

4.4 卷积网络融合（ConvNet Fusion）

4.5 与其他SOTA模型比较

5. Localization

5.1 训练

5.2 测试

5.3 Localization实验

5.3.1 参数设定

5.3.2 与其他SOTA比较

6. 评价

参考