原文： 超详细的语义分割中Loss盘点 - 2020.01.23

作者：GiantPandaCV - 微信公众号

主要涉及图像语义分割任务中所涉及到的目标损失函数.

1. CrossEntropy Loss

CrossEntropyLoss：

$$ L = -\sum_{c=1}^{M} y_c log(p_c) $$

其中，$M$ 表示类别数，$y_c$ 是一个 one-hot 向量，元素只有 0 和 1 两种取值. 如果该类别和样本的类别相同则取值 1，否则为 0. $p_c$ 表示预测样本属于类别 $c$ 的概率.

当 $M=2$ 时，上式就变为二值交叉熵损失函数.

Pytorch - 官方损失函数汇总 - 3/4/6

机器学习 - 交叉熵Cross Entropy - AIUAI

交叉熵损失函数适用于大多数语义分割场景中. 但其一个明显缺点是：对于只分割前景和背景时，当前景像素的数量远远小于背景像素的数量时，即$y=0$ 的数量远大于 $y=1$ 的数量时，数据样本严重不均衡，损失函数中$y=0$ 的背景占据主导作用，导致模型严重偏向于背景，导致效果不好.

Pytorch 示例：

import torch
import torch.nn as nn
import torch.nn.functional as F

#二值交叉熵，这里输入要经过sigmoid处理
nn.BCELoss(F.sigmoid(input), target)

#多分类交叉熵, 用这个 loss 前面不需要加 Softmax 层
nn.CrossEntropyLoss(input, target)

2. Weights CrossEntropy Loss

Weights CrossEntropyLoss：

$$ L = -\sum_{c=1}^{M} w_c y_c log(p_c) $$

该loss 是在 CrossEntropyLoss 的基础上，为每一个类别添加了一个权重参数 $w_c$. 其中，$w_c = \frac{N-N_c}{N}$. $N$ 表示像素总数，$N_c$ 表示类别 $c$ 的像素数.

相比于 CrossEntropyLoss，Weights CrossEntropyLoss 能够对于样本数量不均衡的场景获得更好的效果.

3. Focal Loss

Focal Loss 是在 RetinaNet 论文中提出来解决难易样本数量不均衡问题的.

Focal Loss 论文理解及公式推导 - AIUAI

简单回顾下，

One-Stage的目标检测器通常会产生 10k 数量级的框，但只有极少数是正样本，正负样本数量非常不平衡. 在计算分类的时候常用的交叉熵损失函数的公式如下：

$$ CE(x, y) = \begin{cases} -log(p) &\text{if } y=1 \\ -log(1-p) &\text{otherwise } \end{cases} $$

为了解决正负样本不平衡的问题，往往在二值交叉熵损失函数前加一个权重参数 $\alpha$:

$$ CE = \begin{cases} -\alpha log(p) &\text{if } y=1 \\ -(1-\alpha)log(1-p) &\text{if } y=0 \end{cases} $$

虽然权重参数 $\alpha$ 能够平衡正负样本的数量，但实际上在目标检测中大量的候选目标都是易分样本. 这些样本的损失值很低，但由于数量的极端不平衡，易分样本的数量相对太多，最终占据总损失函数的主导地位.

RetinaNet 论文认为 易分样本(即，置信度高的样本)对模型的提升效果非常小，模型应该主要关注与那些难分样本 . 所以提出只需将高置信度样本的损失降低一些即可. 即 Focal Loss：

$$ FL = \begin{cases} -(1-p)^{\gamma} log(p) &\text{if } y=1 \\ -p^{\gamma}log(1-p) &\text{if } y=0 \end{cases} $$

以 $\gamma=2$ 为例，如果 $p=0.9$，则 $(1-p)^2 = 0.001$，损失函数降低了 1000 倍.

进一步的，结合公式 (4)，同时利用公式(5) 的难易样本的不均衡和公式(4)正负样本的不均衡，得到如下 Focal Loss：

$$ FL = \begin{cases} -\alpha(1-p)^{\gamma} log(p) &\text{if } y=1 \\ -(1-\alpha)p^{\gamma}log(1-p) &\text{if } y=0 \end{cases} $$

如 RetinaNet 的图中展示了 FocalLoss取不同的 $\gamma$ 值时的损失函数下降情况：

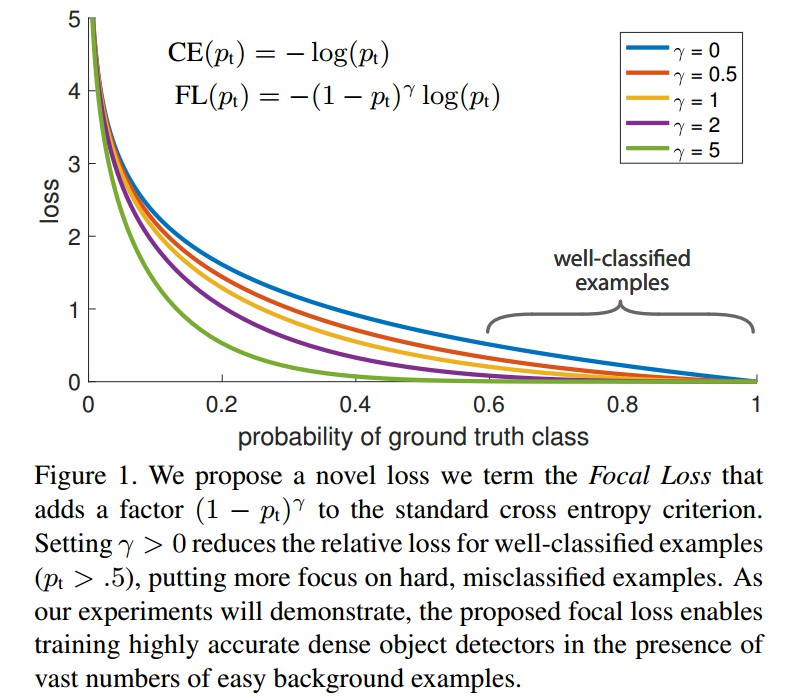
实验结果表明，$\gamma=2, \alpha=0.75$ 时，效果最好. 这样损失函数训练的过程中关注的样本优先级就是正难>负难>正易>负易.

虽然在RetinaNet中取是最好的，但是不代表这个参数在分割任务和其他样本上是最好的. 需要手动调整这个参数，另外Focal Loss在分割任务上似乎是只适合于二分类的情况.

Focal Loss的Pytorch代码实现如下：

class FocalLoss(nn.Module):
    def __init__(self, gamma=0, alpha=None, size_average=True):
        super(FocalLoss, self).__init__()
        self.gamma = gamma
        self.alpha = alpha
        if isinstance(alpha,(float,int,long)): 
            self.alpha = torch.Tensor([alpha,1-alpha])
        if isinstance(alpha,list): 
            self.alpha = torch.Tensor(alpha)
        self.size_average = size_average

    def forward(self, input, target):
        if input.dim()>2:
            # N,C,H,W => N,C,H*W
            input = input.view(input.size(0),input.size(1),-1) 
            # N,C,H*W => N,H*W,C
            input = input.transpose(1,2)   
            # N,H*W,C => N*H*W,C
            input = input.contiguous().view(-1,input.size(2))
        target = target.view(-1,1)

        logpt = F.log_softmax(input)
        logpt = logpt.gather(1,target)
        logpt = logpt.view(-1)
        pt = Variable(logpt.data.exp())

        if self.alpha is not None:
            if self.alpha.type()!=input.data.type():
                self.alpha = self.alpha.type_as(input.data)
            at = self.alpha.gather(0,target.data.view(-1))
            logpt = logpt * Variable(at)

        loss = -1 * (1-pt)**self.gamma * logpt
        if self.size_average: 
            return loss.mean()
        else: 
            return loss.sum()

4. Dice Loss

医学图像分割之 Dice Loss - AIUAI

[1] - Dice系数

Dice系数是用来度量集合相似度的度量函数，通常用于计算两个样本的相似度(值范围为 [0, 1])：

$$ s = \frac{2|X \bigcap Y|}{|X \bigcup Y|} $$

针对图像分割任务来说，$X$ 表示的就是Ground Truth分割图像，$Y$ 表示的是预测的分割图像.

此外，Dice 系数还可以表示为：

$$ s = \frac{2TP}{2TP+FN+FP} $$

其中，$TP$、$FP$ 和 $FN$ 分别代表真阳性，假阳性，假阴性的像素数.

[2] - DiceLoss

$$ Loss = 1 - \frac{2|X \bigcap Y|}{|X \bigcup Y|} $$

Dice Loss使用与样本极度不均衡的情况，如果一般情况下使用Dice Loss会回反向传播有不利的影响，使得训练不稳定.

[3] - 训练分割网络，例如FCN，UNet是选择交叉熵Loss还是选择Dice Loss?

(1) - 假设用 $p$ 表示预测值，$t$ 表示真实标签值，那么交叉熵损失函数关于的梯度形式类似于 $p-t$；而Dice Loss的值是 $1 - \frac{2pt}{p^2 + t^2}$ 或 $1 - \frac{2pt}{p + t}$，其关于 $p$ 的梯度形式为 $\frac{2t^2}{(p+t)^2}$ 或 $\frac{2t(t^2-p^2)}{(p^2+t^2)^2}$. 可以看到在极端情况下即 $p$ 和 $t$ 都很小的时候，计算得到的梯度值可能会非常大，即会导致训练十分不稳定.

(2) - 另外一种解决类别不平衡的方法是简单的对每一个类别根据赋予不同的权重因子(如对数量少的类别赋予较大的权重因子)，使得样本数量不均衡问题得到缓解(上面已经介绍过了，就是带权重的交叉熵Loss).

这两种处理方式，哪种更好，还是建议尝试下.

DiceLoss 的实现：

import torch.nn as nn
import torch.nn.functional as F

class SoftDiceLoss(nn.Module):
    def __init__(self, weight=None, size_average=True):
        super(SoftDiceLoss, self).__init__()
 
    def forward(self, logits, targets):
        num = targets.size(0)
        #为了防止除0的发生
        smooth = 1
        
        probs = F.sigmoid(logits)
        m1 = probs.view(num, -1)
        m2 = targets.view(num, -1)
        intersection = (m1 * m2)
 
        score = 2. * (intersection.sum(1) + smooth) / (m1.sum(1) + m2.sum(1) + smooth)
        score = 1 - score.sum() / num
        return score

5. IoU Loss

IoU Loss 和 Dice Loss 一样，属于 metric learning 的衡量方式，其定义：

$$ L = 1 - \frac{A \bigcap B}{A \bigcup B} $$

IoU Loss 和 Dice Loss 一样存在训练过程中不稳定的问题.

IoU Loss 在图像分割任应用较少. IoU Loss 的代码只需在 Dice Loss 的基础上修改下分母部分即可.

将IOU loss应用到FCN上在VOC 2010上的实验结果：

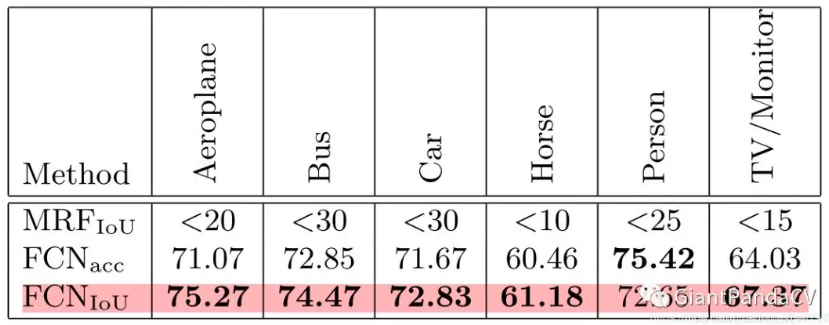
可以看到IOU Loss是对大多数类别的分割结果有一定改善的，但是对Person类却性能反而下降了.

6. Tversky Loss

论文：https://arxiv.org/pdf/1706.05721.pdf

实际上Dice Loss只是Tversky loss的一种特殊形式而已.

Tversky 系数的定义，它是 Dice系数和 Jaccard系数（就是IOU系数，即$\frac{A \bigcap B}{A \bigcup B}$）的广义系数, 公式为：

$$ T(A, B) = \frac{A \bigcap B}{A \bigcap B + \alpha |A - B| + \beta |B-A|} $$

其中，$A$ 和 $B$ 分别表示预测值和真值. 当 $\alpha=\beta=0.5$ 时，即为 Dice 系数. 当 $\alpha=\beta=1$ 时，即为 Jaccard系数。

其中，$A-B$ 表示 FP(假阳性), $|B - A|$ 表示FN (假阴性). 通过调整 $\alpha$ 和 $\beta$ 参数来控制两者之间的平衡, 进而影响召回率等指标.

下表展示了对FCN使用 Tversky Loss 进行病灶分割，并且取不同的和参数获得的结果，其中Sensitivity代表召回率Recall，而Specificity表示准确率Precision：

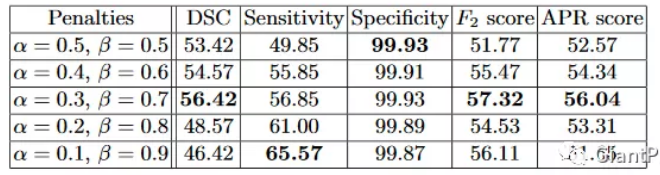
在极小的病灶下的分割效果图如下：

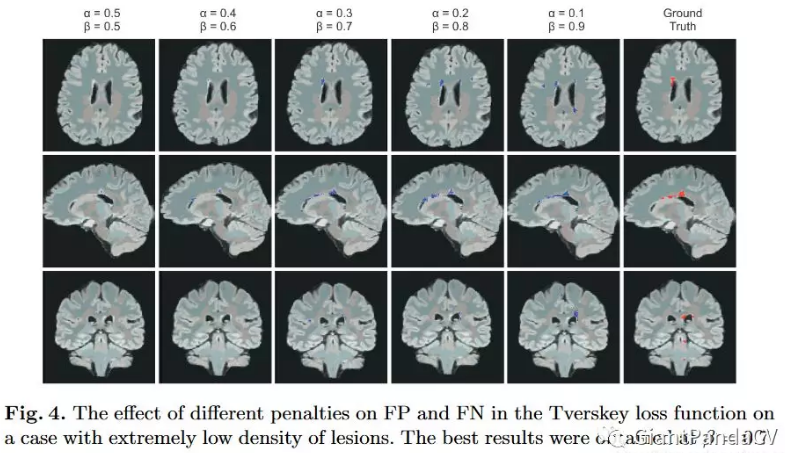
而在较大的病灶下的分割效果图如下：

Keras 实现如：

def tversky(y_true, y_pred):
    y_true_pos = K.flatten(y_true)
    y_pred_pos = K.flatten(y_pred)
    true_pos = K.sum(y_true_pos * y_pred_pos)
    false_neg = K.sum(y_true_pos * (1-y_pred_pos))
    false_pos = K.sum((1-y_true_pos)*y_pred_pos)
    alpha = 0.7
    return (true_pos + smooth)/(true_pos + alpha*false_neg + (1-alpha)*false_pos + smooth)

def tversky_loss(y_true, y_pred):
    return1 - tversky(y_true,y_pred)

7. Generalized Dice loss

论文：Generalized Overlap Measures for Evaluation and Validation in Medical Image Analysis

Generalized Dice loss 代码实现：https://github.com/keras-team/keras/issues/9395

刚才分析过 Dice Loss对小目标的预测是十分不利的，因为一旦小目标有部分像素预测错误，就可能会引起Dice系数大幅度波动，导致梯度变化大训练不稳定.

另外从上面的代码实现可以发现，Dice Loss针对的是某一个特定类别的分割的损失. 当类似于病灶分割有多个场景的时候一般都会使用多个Dice Loss，所以Generalized Dice loss就是将多个类别的Dice Loss进行整合，使用一个指标作为分割结果的量化指标.

GDL Loss在类别数为2时公式如下：

$$ GDL = 1-2\frac{\sum_{l=1}^2 w_l \sum_n r_{ln} p_{ln}}{\sum_{l=1}^2 w_l \sum_n r_{ln} + p_{ln}} $$

其中，$r_{ln}$ 表示类别 $l$ 在第 $n$ 个位置的真实像素类别；$p_{ln}$ 表示对应的预测概率值. $w_l$ 表示每个类别的权重. $w_l = \frac{1}{\sum_{i=1}^n r_{ln}^2}$.

Keras 实现：

def generalized_dice_coeff(y_true, y_pred):
    Ncl = y_pred.shape[-1]
    w = K.zeros(shape=(Ncl,))
    w = K.sum(y_true, axis=(0,1,2))
    w = 1/(w**2+0.000001)
    # Compute gen dice coef:
    numerator = y_true*y_pred
    numerator = w*K.sum(numerator,(0,1,2,3))
    numerator = K.sum(numerator)
    denominator = y_true+y_pred
    denominator = w*K.sum(denominator,(0,1,2,3))
    denominator = K.sum(denominator)
    gen_dice_coef = 2*numerator/denominator
    return gen_dice_coef

def generalized_dice_loss(y_true, y_pred):
    return1 - generalized_dice_coeff(y_true, y_pred)

8. BCE + Dice Loss

将BCE Loss和Dice Loss进行组合，在数据较为均衡的情况下有所改善，但是在数据极度不均衡的情况下交叉熵Loss会在迭代几个Epoch之后远远小于Dice Loss，这个组合Loss会退化为Dice Loss.

9. Focal Loss + Dice Loss

这个Loss的组合应该最早见于腾讯医疗AI实验室2018年在《Medical Physics》上发表论文:

https://arxiv.org/pdf/1808.05238.pdf

腾讯医疗AI实验室和美国加州大学联合发布最新研究 - 2018.11.15

论文提出了使用Focal Loss和Dice Loss来处理小器官的分割问题。公式如下：

$$ TP_p(c) = \sum_{n=1}^N p_n(c) g_n(c) $$

$$ FN_p(c) = \sum_{n=1}^N (1 - p_n(c)) g_n(c) $$

$$ FP_p(c) = \sum_{n=1}^N p_n(c)(1 - g_n(c)) $$

$$ \mathcal{L} = \mathcal{L}_{Dice} + \lambda \mathcal{L}_{Focal} $$

$$ \mathcal{L} = C - \sum_{c=0}^{C-1} \frac{TP_p(c)}{TP_p(c) + \alpha FN_p(c) + \beta FP_p(c)} - \lambda \frac{1}{N} \sum_{c=0}^{C-1} \sum_{n=1}^{N}g_n(c)(1 - p_n(c))^2log(p_n(c)) $$

其中，$TP_p(c)$， $FN_p(c)$, $FP_p(c)$ 分别表示对于类别 $c$ 的真阳性，假阴性，假阳性.

可以看到这里使用Focal Loss的时候，里面的两个参数直接用对于类别 $c$ 的正样本像素个数来代替. 具体实验细节和效果可以去看看原论文.

10. Exponential Logarithmic loss

MICCAI 2018 论文 3D Segmentation with Exponential LogarithmicLoss for Highly Unbalanced Object Sizes 所提出来的. 其结合了 Focal Loss以及Dice loss:

$$ L_{Exp} =w_{Dice}L_{Dice} + w_{Cross}L_{Cross} $$

新增了两个权重参数：$w_{Dice}$ 和 $w_{Cross}$. $L_{Dice}$ 表示指数 log Dice 损失，$L_{Cross}$ 表示指数交叉熵损失.

$$ L_{Dice} = \mathbf{E}[(-ln(Dice_i))^{\gamma Dice}] $$

$$ Dice_i = \frac{2(\sum_{\mathbf{x}}\sigma_{il}(\mathbf{x})p_i(\mathbf{x})) + \epsilon}{(\sum_{\mathbf{x}}\sigma_{il}(\mathbf{x}) + p_i(\mathbf{x})) + \epsilon} $$

$$ L_{Cross} = \mathbf{E}[w_l(-ln(p_l(\mathbf{x})))^{\gamma Cross}] $$

其中，$x$ 表示像素位置，$i$ 表示类别标签, $l$ 表示像素位置 $x$ 处的 groundtruth 类别, $p_i(x)$ 表示经过 Softmax 操作后的概率值.

其中，$w_l = (\frac{\sum_k f_k}{f_l})^{0.5}$. $f_k$ 表示类别标签 $k$ 出现的概率，该参数可以减少出现频率较高的类别权重.

其中，$\gamma Dice$ 和 $\gamma Cross$ 可以提升函数的非线性. 如图：

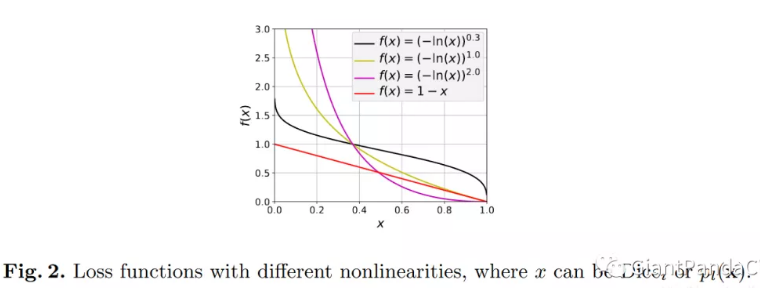
11. Lovasz-Softmax Loss

CVPR2018 论文 The Lovasz-Softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks 中所提出的，Kaggle 神器.

Github - LovaszSoftmax 给出了Pytorch 和 Tensorflow 的实现.

HomePage - LovaszSoftmax

Lovasz-Softmax Loss是对 Jaccard(IOU) Loss进行 Lovaze扩展，表现更好.

12. 补充 - Softmax 梯度计算

Softmax 函数，如：

$$ S_i = \frac{e^{z_i}}{\sum_k e^{z_k}} $$

全连接层输出，如：

$$ z_i = \sum_{ij} x_{ij} + b $$

全连接层输出加Softmax函数，如：

$$ a_i = \frac{e^{z_i}}{\sum_k e^{z_k}} $$

交叉熵函数：

$$ C = -\sum_i y_i ln a_i $$

其中，$y_i$ 表示真实的标签值.

CS231N 给出一份代码实现：

#coding=utf-8
import numpy as np

def softmax_loss_native(W, X, y, reg):
    '''
    Softmax_loss的暴力实现，利用for循环
    输入的维度是D，有C个分类类别，在有N个例子的batch上进行操作
    输入:
    - W: 一个numpy array，形状是(D, C)，代表权重
    - X: 一个形状为(N, D)为numpy array，代表输入数据
    - y: 一个形状为(N,)的numpy array，代表类别标签
    - reg: (float)正则化参数
    f返回:
    - 一个浮点数代表Loss
    - 和W形状一样的梯度
    '''
    loss = 0.0
    dW = np.zeros_like(W) #dW代表W反向传播的梯度
    num_classes = W.shape[1]
    num_train = X.shape[0]
    for i in xrange(num_train):
        scores = X[i].dot(W)
        shift_scores = scores - max(scores) #防止数值不稳定
        loss_i = -shift_scores[y[i]] + np.log(sum(np.exp(shift_scores)))
        loss += loss_i
        for j in xrange(num_classes):
            softmax_output = np.exp(shift_scores[j]) / sum(np.exp(shift_scores))
            if j == y[i]:
                dW[:, j] += (-1 + softmax_output) * X[i]
            else:
                dW[:, j] += softmax_output * X[i]
    loss /= num_train
    loss += 0.5 * reg * np.sum(W * W)
    dW = dW / num_train + reg * W
    return loss, dW

def softmax_loss_vectorized(W, X, y, reg):
    loss = 0.0
    dW = np.zeros_like(W)
    num_class = W.shape[1]
    num_train = X.shape[0]
    scores = X.dot(W)
    shift_scores = scores - np.max(scores, axis=1).reshape(-1, 1)
    softmax_output  = np.exp(shift_scores) / np.sum(np.exp(shift_scores), axis=1).reshape(-1, 1)
    loss = -np.sum(np.log(softmax_output[range(num_train), list(y)]))
    loss /= num_train
    loss += 0.5 * reg * np.sum(W * W)
    dS = softmax_output.copy()
    dS[range(num_train), list(y)] += -1
    dW = (x.T).dot(dS)
    dW = dW/num_train + reg*W
    return loss, dW