论文: Deep Metric Learning via Lifted Structured Feature Embedding - CVPR2016
作者: Hyun Oh Song, Yu Xiang, Stefanie Jegelka, Silvio Savarese
团队: Stanford University, MIT
样本间距离度量方法, 特征学习
出发点:
[1] - 学习样本语义特征嵌入,使得在语义嵌入空间中,相似样本映射距离更接近,不相似样本映射距离更远.
[2] - 更好的利用网络训练中 batch 训练的优势,提出将一个 batch 内样本的成对距离向量升级为成对距离矩阵(lifting the vector of pairwise distances within the batch to the matrix of pairwise distances).
[3] - 问题被转化为了一个 multiclass label 问题.
1. Introduction
度量学习和降维技术,旨在学习语义距离度量和嵌入,以使相似的样本被映射为流形中邻近点,不相似的样本被映射为距离较远的点.
给定输入图像的标签标注信息,通过训练神经网络结构,直接学习输入图像到低维嵌入之间的非线性映射函数. 网络的优化目标是将不同类的样本间的距离变大,相同类的样本间的距离变小. 判别地训练的网络模型对特征表示和语义嵌入联合训练,对类间变化更加鲁棒.
现有方法不能充分利用网络 mini-batch SGD 训练中 training batches 的优势. 主要是首先随机采样 pairs 或 triplets,以构建 training batch,再对 training batch 中各独立的 pairs 或 triplets 计算 loss.
本文方法将 training batch 内的成对距离向量转化为成对距离矩阵,并设计一种新的结构化损失函数.
首先回顾了基于判别性网络训练来学习语义嵌入的方法.
1.1. Contrastive embedding
对比嵌入是在成对数据 ${ {(\pmb{x_i}, \pmb{x_j}, y_{ij})} }$ 上进行训练的.
contrastive training 最小化相同类别的成对样本间的距离,惩罚 negative 成对距离小于边缘参数 ${ \alpha }$ .
代价函数定义:
$$ { J = \frac{1}{m} \sum_{(i, j)}^{m/2} y_{i, j} D_{i, j}^2 + (1-y_{i,j})[\alpha- D_{i, j}]_{+}^2 } $$
其中,
m - batch 内图片数,即batchsize.
${ f(\cdot) }$ - 网络输出的特征嵌入.
${ D_{i, j} = ||f(\pmb{x}_i)- f(\pmb{x}_j)||_2 }$
${ y_{i, j} \in {0, 1} }$ - 表示一对样本 ${ (\pmb{x}_i, \pmb{x}_j) }$ 是否是同类样本.
${ [\cdot]_+ }$ - 表示 hinge 函数 ${ max(0, \cdot) }$ 操作.
1.2 Triplet embedding
三元组嵌入是在三元组数据 $\lbrace(\pmb{x}_a^{(i)}, \pmb{x}_p^{(i)}, \pmb{x}_n^{(i)})\rbrace$,其中 $\lbrace (\pmb{x}_a^{(i)}, \pmb{x}_p^{(i)})\rbrace$ 是相同类, $\lbrace (\pmb{x}_a^{(i)}, \pmb{x}_n^{(i)}) \rbrace$ 是不同类. ${ {\pmb{x}_a^{(i)}} }$ 是一个三元组中的参考项(anchor).
triplet training 寻找一个语义嵌入,使得 $\lbrace (\pmb{x}_a^{(i)}, \pmb{x}_n^{(i)}) \rbrace$ 间的距离大于 $\lbrace (\pmb{x}_a^{(i)}, \pmb{x}_p^{(i)}) \rbrace$ 间的距离加上一个边缘参数 ${ \alpha }$.
代价函数定义:
$$ { J = \frac{3}{2m} \sum_{i}^{m/3} [D_{ia, ip} ^2- D_{ia, in}^2 + \alpha]_{+} } $$
其中,
$$ { D_{ia, ip} = ||f(\pmb{x}_i^a)- f(\pmb{x}_j^p)|| } $$
$$ { D_{ia, ip} = ||f(\pmb{x}_i^a)- f(\pmb{x}_i^n)|| } $$
如图 Fig2(a) 和 (b).

Figure 2. 六个样本的 training batch 的不同训练例示. 红色线和蓝色线分别表示相似和不相似的样本. 对比而言,Lifted structured embedding 能够考虑 batch 内所有的成对距离.

Figure 3. 不同嵌入方法的训练网络例示. m 表示 batch 内图片数,即batchsize. 绿色框表示一个 batch 的一个样本.
(a) 网络采用二值labels作为输入;
(b) 网络不需要 label 输入,anchor , positive 和 negetive 的顺序编码了 label 信息;
(c) 网络采用 multiclass label 作为输入.
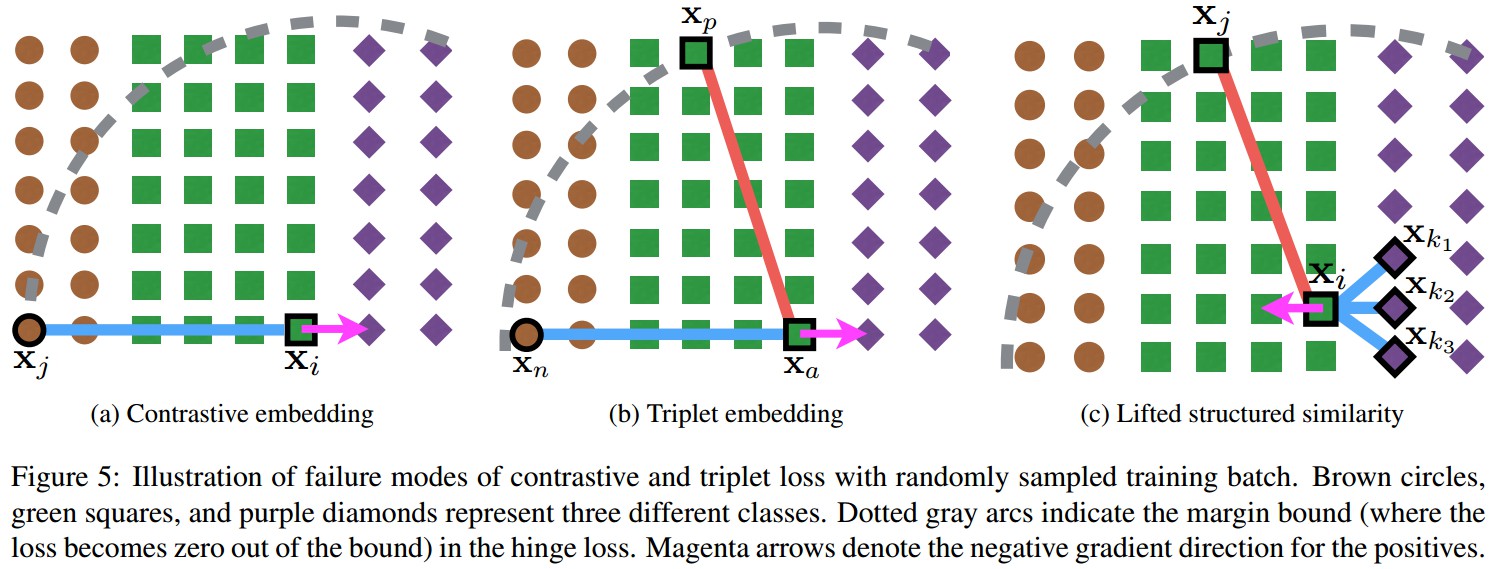
Figure5. 随机对 training batch 采样,采用contrastive loss 和 triplet loss 失败的情况. 这里以三类为例,分别对应棕色圆、绿色方块和紫色棱形. 虚线灰色弧线表示在 hinge loss 中的边界(超出边界后,loss变为0). 品红色箭头表示对于 positives 的 negative 梯度方向.
(a)当随机采样的 negative ${ (\pmb{x}_j) }$ 与其它类的样本共线时,Contrastive embedding 会失败;
(b)当随机采样的 negative ${ (\pmb{x}_n) }$ 相对于 positive ${ (\pmb{x}_p) }$ 和 anchor ${ (\pmb{x}_a) }$,在边界内时,Triplet embedding 会失败;
2. Lifted structured feature embedding
基于训练集中的所有 positive 和 negetive 样本定义 loss 函数: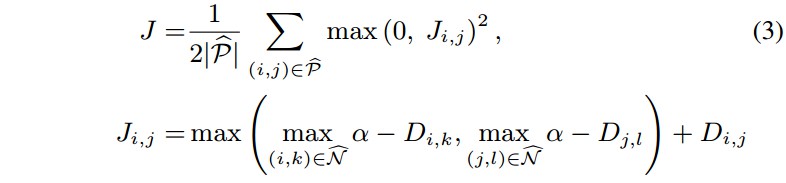
其中,
${ \check{P} }$ - 训练集中的 positive 样本对 集合
${ \check{N} }$ - 训练集中的 negative 样本对 集合
该 loss 函数面临的计算上的挑战:
- 非平滑
- 函数的估计和其 subgradient 的计算需要对所有的样本对进行多次最小化.
解决方案:
- 1 - 对函数的平滑上边界进行优化;
- 2 - 采用随机(stochastic)方法对大数据集处理.
启发点:
- 1 - 偏向于对“困难”样本对,正如 $J_{i,j}$ 的 subgradient 计算 采用的接近的 negative pairs. (it biases the sample towards including “difficult” pairs, just like a subgradient of Ji;j would use the close negative pairs).
- 2 - 对一次采样的 mini-batch 内的所有样本信息进行利用,而不仅是单独的样本对.
key idea:
- 加速 mini-batch 的优化,以充分利用 batch 内的全部 $O(m^2)$ 对样本信息 .
给定 batch 的 c 维特征 ${ X \in R^{m×c} }$,及 batch内各元素的二次方范数列向量 ${ \check{\pmb{x}} = [||f(\pmb{x}_1)||_2^2, ..., ||f(\pmb{x}_m)||_2^2]^T }$
即可构建密集平方距离对矩阵(dense pairwise squared distance matrix):
${ D^2 = \check{\pmb{x}} \pmb{1}^T + \pmb{1} \check{\pmb{x}}^T- 2XX^T }$
${ D_{ij}^2 = ||f(\pmb{x}_i)- f(\pmb{x}_j)||_2^2 }$
需要注意的是,随机采样的样本对的 negative edges 具有有限的信息.
这里提出的方法并不是完全随机采样的,而是引入重要性采样元素. 随机的采样一些 positive 样本对,再对其添加一些 difficult neighbors 来训练 mini-batch. 这种处理添加了 subgradient 采用的相关信息.
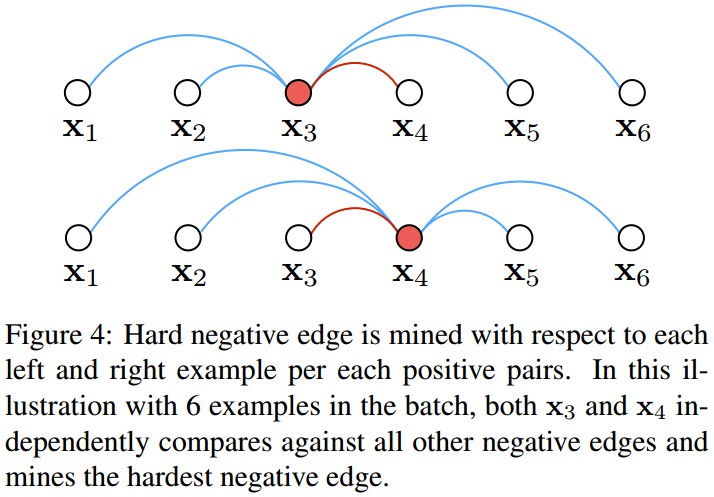
Figure 4. 对于各 positive pairs的每个样本,找出其左右的 hard negative edge. batch内有 6 个样本,x3 和 x4 分别与所有的其它 negative edges进行比较,以找到 hardest negative edge.
由于采用嵌套的 max 函数来寻找单个 hardest negative 往往导致网络收敛到一个 bad 局部最优解. 因此,这里采取优化其平滑上界 ${ \check{J}(D(f(\pmb{x}))) }$. 针对各 batch, loss 函数定义如下: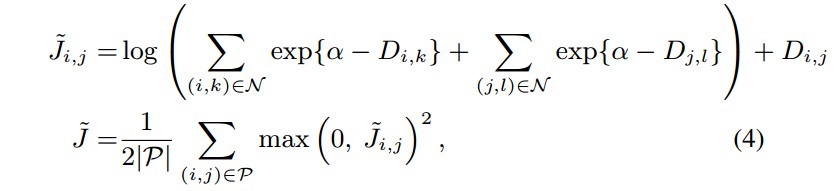
BP计算过程:
其中,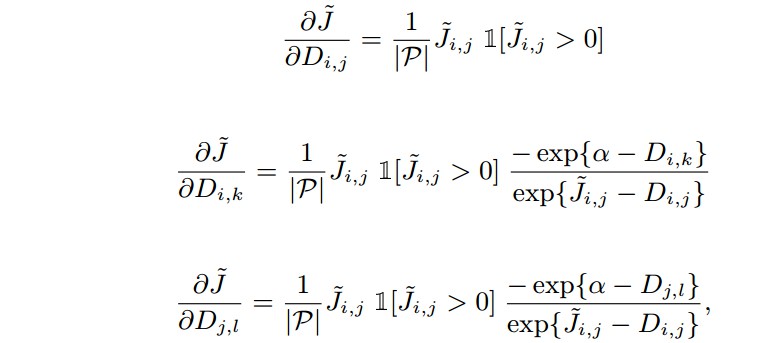
3. Results
成功的:
失败的:
Reference
[1] - Learning visual similarity for product design with convolutional neural networks
[2] - Dimensionality reduction by learning an invariant mapping
[3] - Facenet: A unified embedding for face recognition and clustering