Hingeloss 用于计算 one-of-many 分类任务.

<h2>1. Hinge Loss 概念</h2>

定义为：

${E(z) = max(0, 1-z)}$

常用在SVM的最大化间隔分类中.

对于期望输出 ${t=&#92;{+1,-1&#92;}}$和分类器 ${y}$， 预测值 ${\hat{y}}$ 的 hinge loss 为：

${y = max(0, 1-t&#42;y)}$

这里，y 应该是分类器决策函数的原是输出，而不是预测的最终类别结果.

例如，线性SVMs，${y=w&#42;x+b}$，其中 (w,b) 是超平面的参数，x为待分类的点.

当 t 和 y 符号相同(即 y预测到正确的类别)和 ${|y|>=1}$ 时， hinge loss: ${l(y)=0}$；

当 t 和 y 符号相反时，hinge loss ${l(y)}$ 则随着 y的增加而线性增加(one-side error).

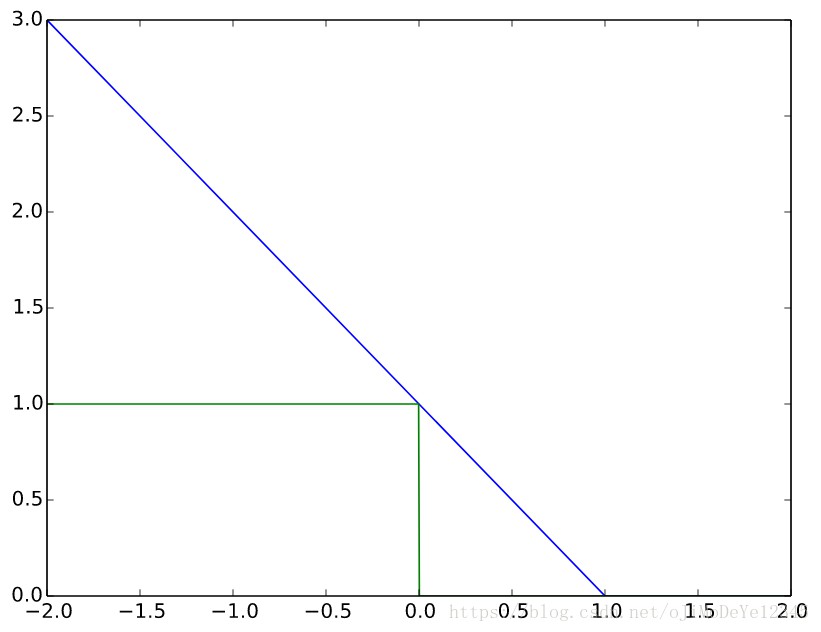
$t=1时，针对变量 y，其hinge loss(蓝色线) vs. zero-one loss(青色，misclassification).

Note that the hinge loss penalizes predictions y < 1, corresponding to the notion of a margin in a support vector machine(SVM).

<h2>2. Caffe HingeLossLayer 参数</h2>

输入 Blob 向量(2 个)

• bottom[0] - (NxCxHxW), 预测值 t，其各值表示 K=CHW 类中的每一个类别的预测分数.

在SVM中，t 是 D-维特征 ${X \in R^{D×K}} $ 和学习超平面参数 ${W \in R^{D×K}} $ 作为输入，进行内积计算 $ {X^TW}$ 得到的结果， 故 HingeLossLayer 采用 InnerProductLayer(num_output=D)的预测值作为输入，不需要再学习参数及其它loss计算，即等价于线性SVM(一个全连接层加上一个Hingeloss相当于一个线性SVM).

• bottom[1] - (Nx1x1x1), labels ${t}$，其值为整数，${l_n=[0,1,2,...,K-1]}$，分别表示所对应的 K 个类别中正确的类别标签.

输出 Blob 向量(1 个)

• top[0] - (1x1x1x1)，计算得到的 hinge loss：

${E = \frac{1}{N}\sum_{n=1}^N\sum_{k=1}^K[max(0, 1- \sigma(l_n=k)*t_{nk})]^p }$

其中, ${L^p}$ 范数，p=1 - L1 范数；p=2 - L2 范数，类似于 L2-SVM；
如果 condition 为 True， 即条件成立， 则 ${\sigma(condition) = 1}$；否则，${\sigma(condition) = -1}$.

<h2>3. Caffe prototxt定义</h2>

......
layer {
  name: "fc8voc"
  type: "InnerProduct"
  bottom: "fc7"
  top: "fc8voc"
  param {
    lr_mult: 10
    decay_mult: 1
  }
  param {
    lr_mult: 2
    decay_mult: 0
  }
  inner_product_param {
    num_output: 20
    weight_filler {
      type: "gaussian"
      std: 0.01
    }
    bias_filler {
      type: "constant"
      value: 0
    }
  }
}

layer {
  name: "loss"
  type: "HingeLossMultiLabel"
  bottom: "fc8voc"
  bottom: "label"
  top: "loss"
}

<h2>Reference</h2>

[0] - Hinge loss - wikipedia
[1] - HingeLossLayer - Caffe
[2] - Analyzing Classifiers: Fisher Vectors and Deep Neural Networks [caffemode] [prototxt]