1. 可分离卷积提出背景
传统的卷积神经网络在计算机视觉领域已经取得了非常好的成绩,但是依然存在一个待改进的问题—计算量大。
当卷积神经网络应用到实际工业场景时,模型的参数量和计算量都是十分重要的指标,较小的模型可以高效地进行分布式训练,减小模型更新开销,降低平台体积功耗存储和计算能力的限制,方便部署在移动端。
因此,为了更好地实现这个需求,在卷积运算的基础上,学者们提出了更为高效的可分离卷积。
2. 空间可分离卷积
空间分离卷积(spatial separable convolutions),顾名思义就是在空间维度将标准卷积运算进行拆分,将标准卷积核拆分成多个小卷积核。例如可以将卷积核拆分成两个(或多个)向量的外积:
$$ \left[\begin{array}{ccc} 3 & 6 & 9 \\ 4 & 8 & 12 \\ 5 & 10 & 15 \end{array}\right] = \left[\begin{array}{ccc} 3 \\ 4 \\ 5 \end{array}\right] \times \left[\begin{array}{ccc} 1 \quad 2 \quad 3 \end{array}\right] $$
此时,对于一副输入图像而言,就可以先用$3\times1$的kernel做一次卷积,再用$1\times3$的kernel做一次卷积,从而得到最终结果。具体操作如 图1 所示。
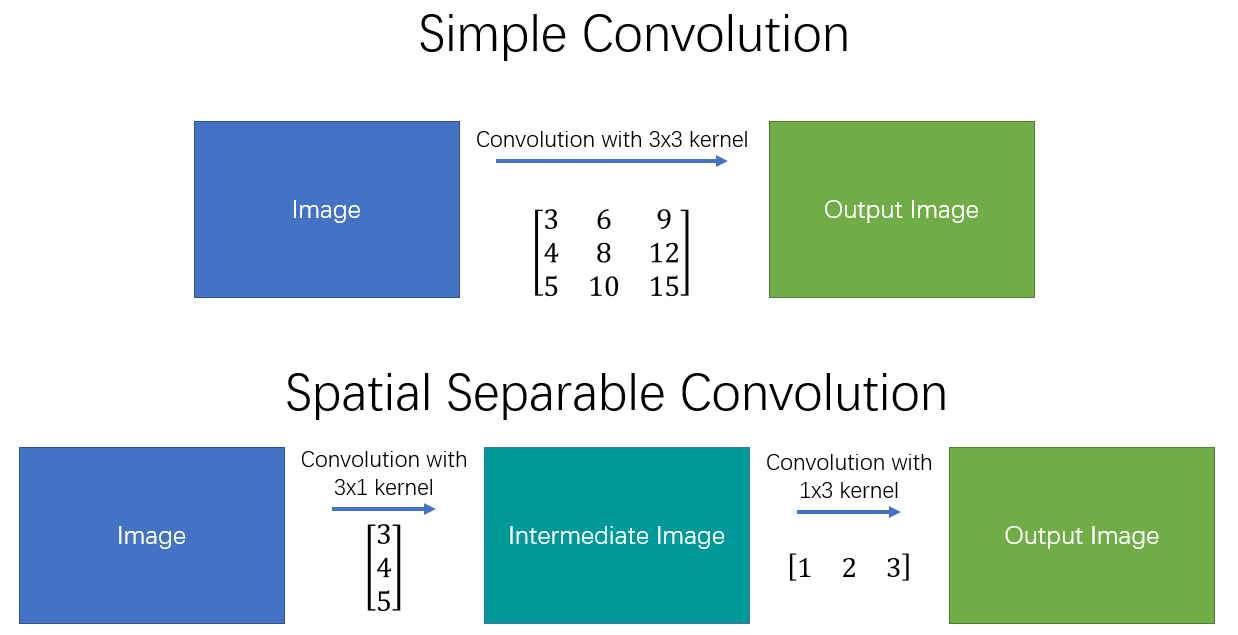
图1 空间可分离卷积
这样,将原始的卷积进行拆分,本来需要9次乘法操作的一个卷积运算,就变为了两个需要3次乘法操作的卷积运算,并且最终效果是不变的。可想而知,乘法操作减少,计算复杂性就降低了,网络运行速度也就更快了。
但是空间可分离卷积也存在一定的问题,那就是并非所有的卷积核都可以拆分成两个较小的卷积核。 所以这种方法使用的并不多。
2.1. 应用示例
空间可分离卷积在深度学习中应用较少,在传统图像处理领域比较有名的是可用于边缘检测的sobel算子,分离的sobel算子计算方式如下:
$$ \left[\begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right] = \left[\begin{array}{ccc} 1 \\ 2 \\ 1 \end{array}\right] \times \left[\begin{array}{ccc} -1 \quad 0 \quad 1 \end{array}\right] $$
3. 深度可分离卷积
深度可分离卷积(depthwise separable convolutions)的不同之处在于,其不仅仅涉及空间维度,还涉及深度维度(即 channel 维度)。通常输入图像会具有3个channel:R、G、B。在经过一系列卷积操作后,输入特征图就会变为多个channel。对于每个channel而言,我们可以将其想成对该图像某种特定特征的解释说明。例如输入图像中,“红色” channel 解释描述了图像中的“红色”特征,“绿色” channel 解释描述了图像中的“绿色”特征,“蓝色” channel 解释描述了图像中的“蓝色”特征。又例如 channel 数量为64的输出特征图,就相当于对原始输入图像的64种不同的特征进行了解释说明。
类似空间可分离卷积,深度可分离卷积也是将卷积核分成两个单独的小卷积核,分别进行2种卷积运算:深度卷积运算和逐点卷积运算。 首先,看看正常的卷积是如何工作的。
3.1. 标准卷积
假设我们有一个 $12\times 12\times 3$ 的输入图像,即图像尺寸为 $12\times 12$,通道数为3,对图像进行 $5\times 5$ 卷积,没有填充(padding)且步长为1。如果我们只考虑图像的宽度和高度,使用 $5\times 5$ 卷积来处理 $12\times 12$ 大小的输入图像,最终可以得到一个 $8\times 8$ 的输出特征图。然而,由于图像有3个通道,我们的卷积核也需要有3个通道。 这就意味着,卷积核在每个位置进行计算时,实际上会执行 $5\times 5\times 3=75$ 次乘法。如 图2 所示,我们使用一个 $5\times 5\times 3$ 的卷积核进行卷积运算,最终可以得到 $8\times 8\times 1$ 的输出特征图。
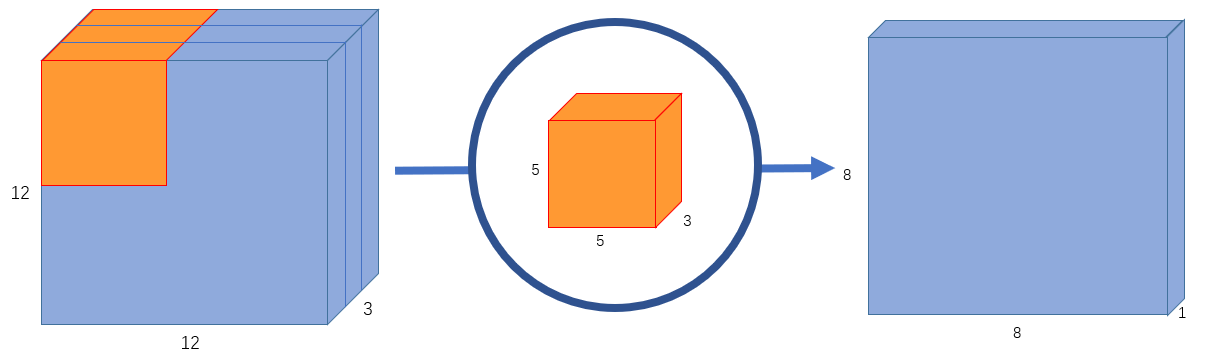
图2 输出通道为1的标准卷积
如果我们想增加输出的 channel 数量让网络学习更多种特征呢?这时我们可以创建多个卷积核,比如256个卷积核来学习256个不同类别的特征。此时,256个卷积核会分别进行运算,得到256个 $8\times 8\times 1$ 的输出特征图,将其堆叠在一起,最终可以得到 $8\times 8\times 256$ 的输出特征图。如 图3 所示。
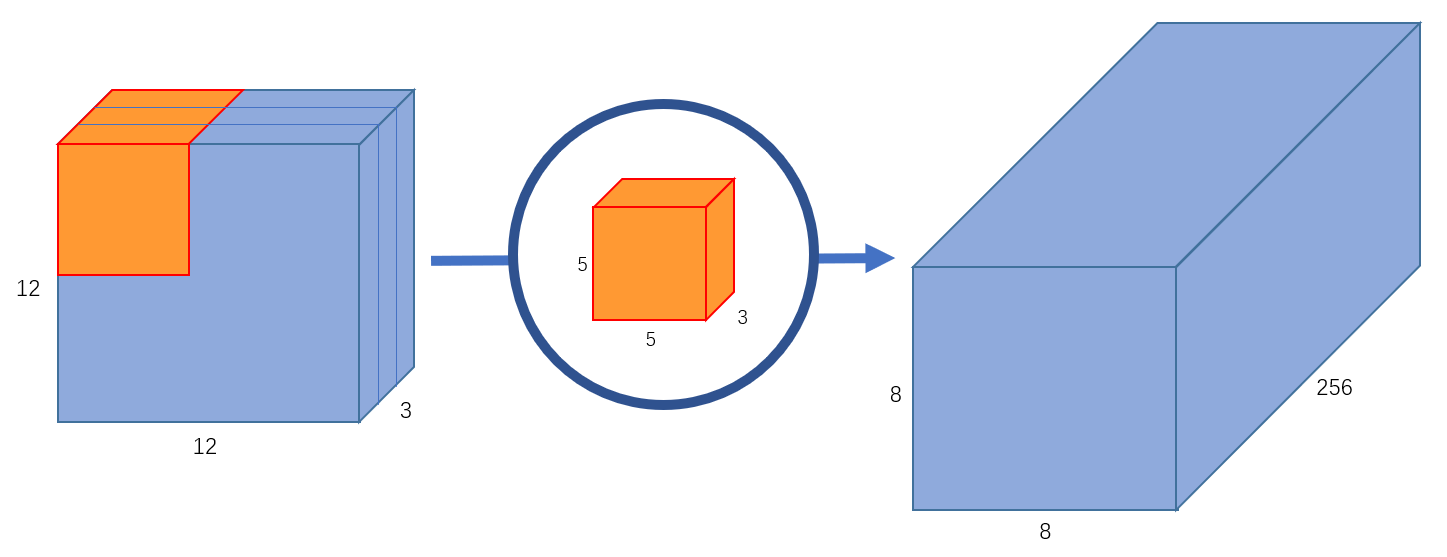
图3 输出通道为256的标准卷积
接下来,再来看一下如何通过深度可分离卷积得到 $8\times 8\times 256$ 的输出特征图。
3.2. 深度卷积运算
首先,我们对输入图像进行深度卷积运算,这里的深度卷积运算其实就是逐通道进行卷积运算。对于一幅 $12\times 12\times 3$ 的输入图像而言,我们使用大小为 $5\times 5$ 的卷积核进行逐通道运算,计算方式如 图4 所示。
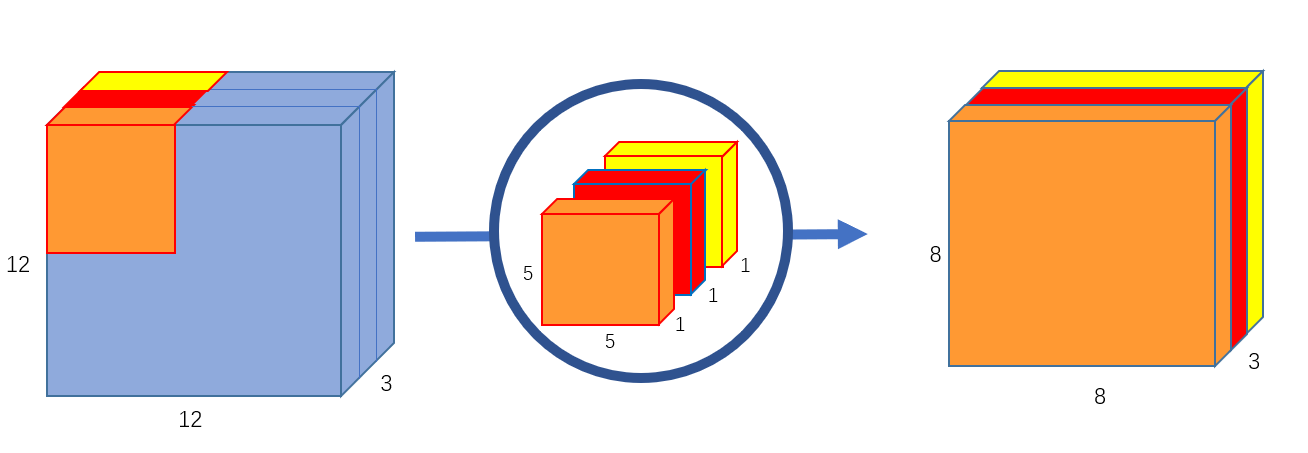
图4 深度卷积运算
这里其实就是使用3个 $5\times 5\times 1$ 的卷积核分别提取输入图像中3个 channel 的特征,每个卷积核计算完成后,会得到3个 $8\times 8\times 1$ 的输出特征图,将这些特征图堆叠在一起就可以得到大小为 $8\times 8\times 3$ 的最终输出特征图。这里我们可以发现深度卷积运算的一个缺点,深度卷积运算缺少通道间的特征融合 ,并且运算前后通道数无法改变。
因此,接下来就需要连接一个逐点卷积来弥补它的缺点。
3.3. 逐点卷积运算
前面我们使用深度卷积运算完成了从一幅 $12\times 12\times 3$ 的输入图像中得到 $8\times 8\times 3$ 的输出特征图,并且发现仅使用深度卷积无法实现不同通道间的特征融合,而且也无法得到与标准卷积运算一致的 $8\times 8\times 256$ 的特征图。那么,接下来就让我们看一下如何使用逐点卷积实现这两个任务。
逐点卷积其实就是 $1\times 1$ 卷积,因为其会遍历每个点,所以我们称之为逐点卷积。 $1\times 1$ 卷积在前面的内容中已经详细介绍了,这里我们还是结合上边的例子看一下它的具体作用。
我们使用一个3通道的 $1\times 1$ 卷积对上文中得到的 $8\times 8\times 3$ 的特征图进行运算,可以得到一个 $8\times 8\times 1$ 的输出特征图。如 图5 所示。此时,我们就使用逐点卷积实现了融合3个通道间特征的功能。
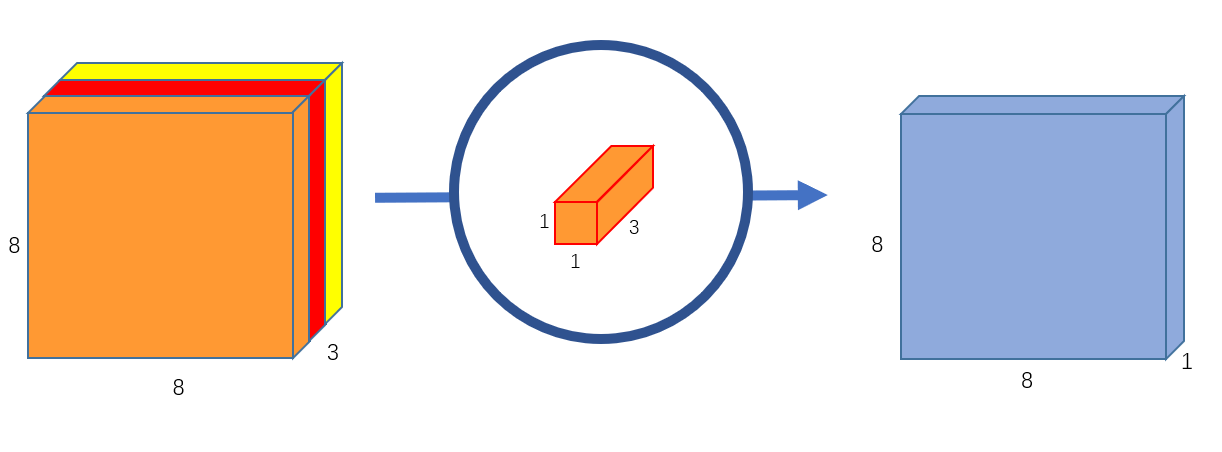
图5 输出通道为1的逐点卷积
此外,我们可以创建256个3通道的 $1\times 1$ 卷积对上文中得到的 $8\times 8\times 3$ 的特征图进行运算,这样,就可以实现得到与标准卷积运算一致的 $8\times 8\times 256$ 的特征图的功能。如 图6 所示。
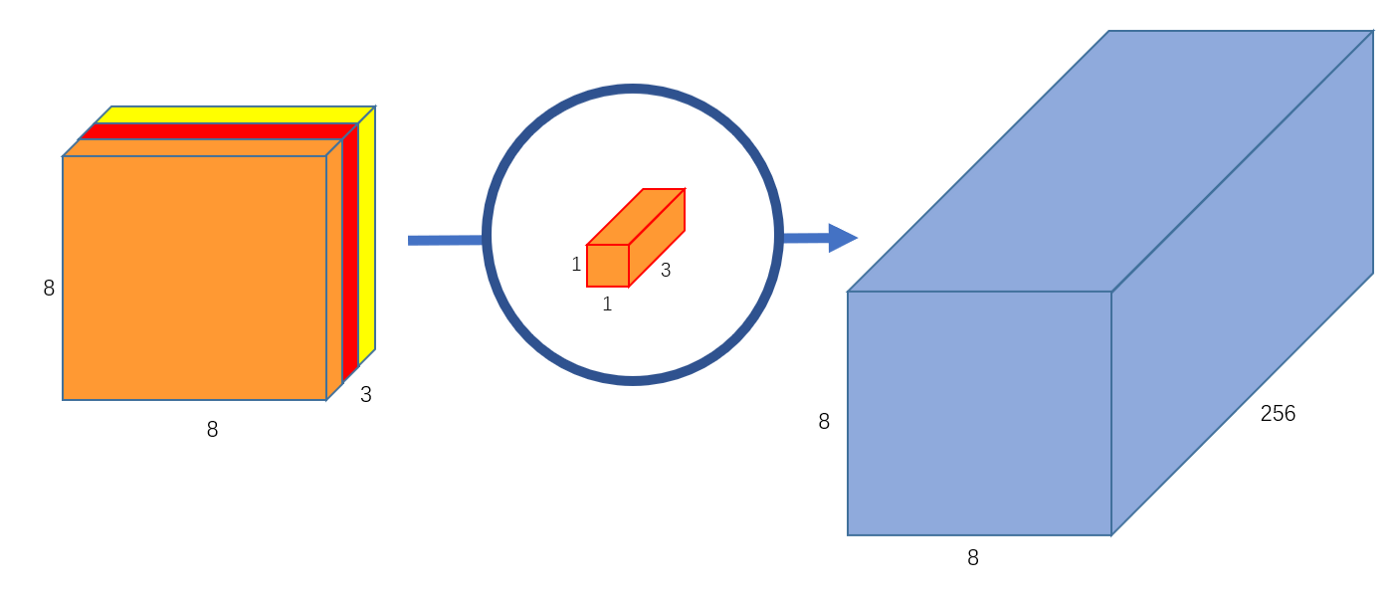
图6 输出通道为256的逐点卷积
3.4. 深度可分离卷积的意义
上文中,我们给出了深度可分离卷积的具体计算方式,那么使用深度可分离卷积代替标准卷积有什么意义呢?
这里我们看一下上文例子中标准卷积的乘法运算个数,我们创建了256个 $5\times 5\times 3$ 的卷积核进行卷积运算,每个卷积核会在输入图片上移动 $8\times 8$ 次,因此总的乘法运算个数为:
$$ 256 \times 3 \times 5 \times 5 \times 8 \times 8=1228800 $$
而换成深度可分离卷积后,在深度卷积运算时,我们使用3个 $5\times 5\times 1$ 的卷积核在输入图片上移动 $8\times 8$ 次,此时乘法运算个数为:
$$ 3 \times 5 \times 5 \times 8 \times 8=4800 $$
在逐点卷积运算时,我们使用256个 $1\times 1\times 3$ 的卷积在输入特征图上移动 $8\times 8$ 次,此时乘法运算个数为:
$$ 256 \times 1 \times 1 \times 3 \times 8 \times 8=49152 $$
将这两步运算相加,即可得到,使用深度可分离卷积后,总的乘法运算个数变为:53952。可以看到,深度可分离卷积的运算量相较标准卷积而言,计算量少了很多。
3.5. 应用示例
MobileNetv1[1]中使用的深度可分离卷积如 图7 右侧所示。相较于左侧的标准卷积,其进行了拆分,同时使用了BN层以及RELU激活函数穿插在深度卷积运算和逐点卷积运算中。
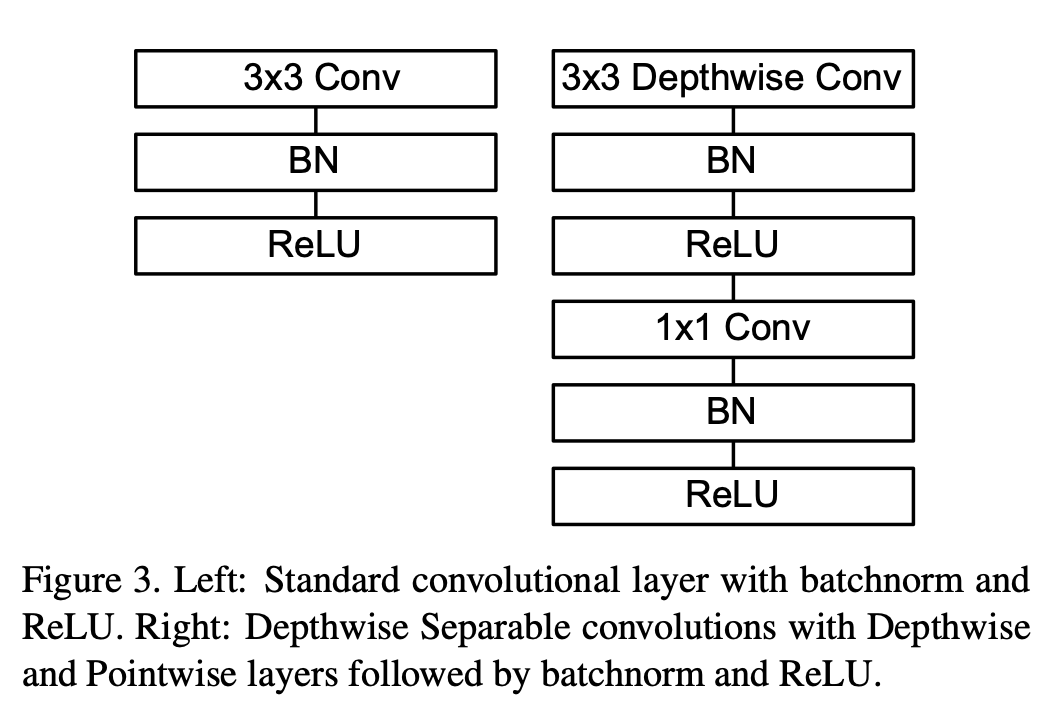
图7 MobileNetv1中的可分离卷积
参考文献
[1] - MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications