1. 什么是激活函数
- 激活函数是人工神经网络的一个极其重要的特征;
- 激活函数决定一个神经元是否应该被激活,激活代表神经元接收的信息与给定的信息有关;
- 激活函数对输入信息进行非线性变换,然后将变换后的输出信息作为输入信息传给下一层神经元。
2. 激活函数的作用
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,最终的输出都是输入的线性组合。
激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数。
3. 激活函数的种类
3.1. identity
函数定义:
$$f(x)=x$$
导数:
$${ f }^{ ' }(x)=1$$
函数图形如 图1 所示:
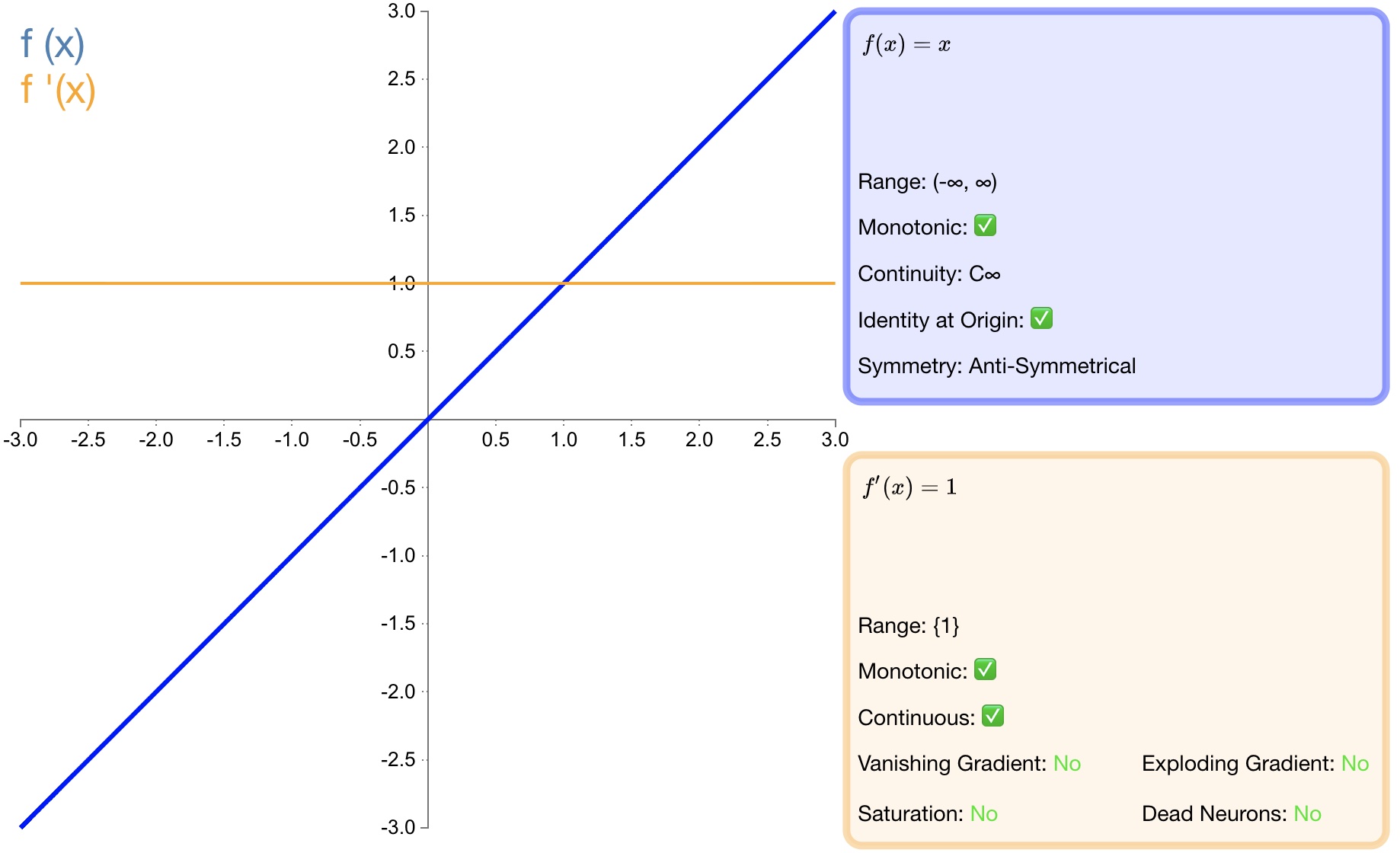
图1 identity
优点:适合于潜在行为是线性(与线性回归相似)的任务。
缺点:无法提供非线性映射,当多层网络使用identity激活函数时,整个网络就相当于一个单层模型。
3.2. step
函数定义:
$$ { f }(x)=\begin{cases} \begin{matrix} 0 & x<0 \end{matrix} \\ \begin{matrix} 1 & x\ge 0 \end{matrix} \end{cases}$$
导数:
$$ { f }^{ ' }(x)=\begin{cases} \begin{matrix} 0 & x\neq 0 \end{matrix} \\ \begin{matrix} ? & x=0 \end{matrix} \end{cases}$$
函数图形如 图2 所示:
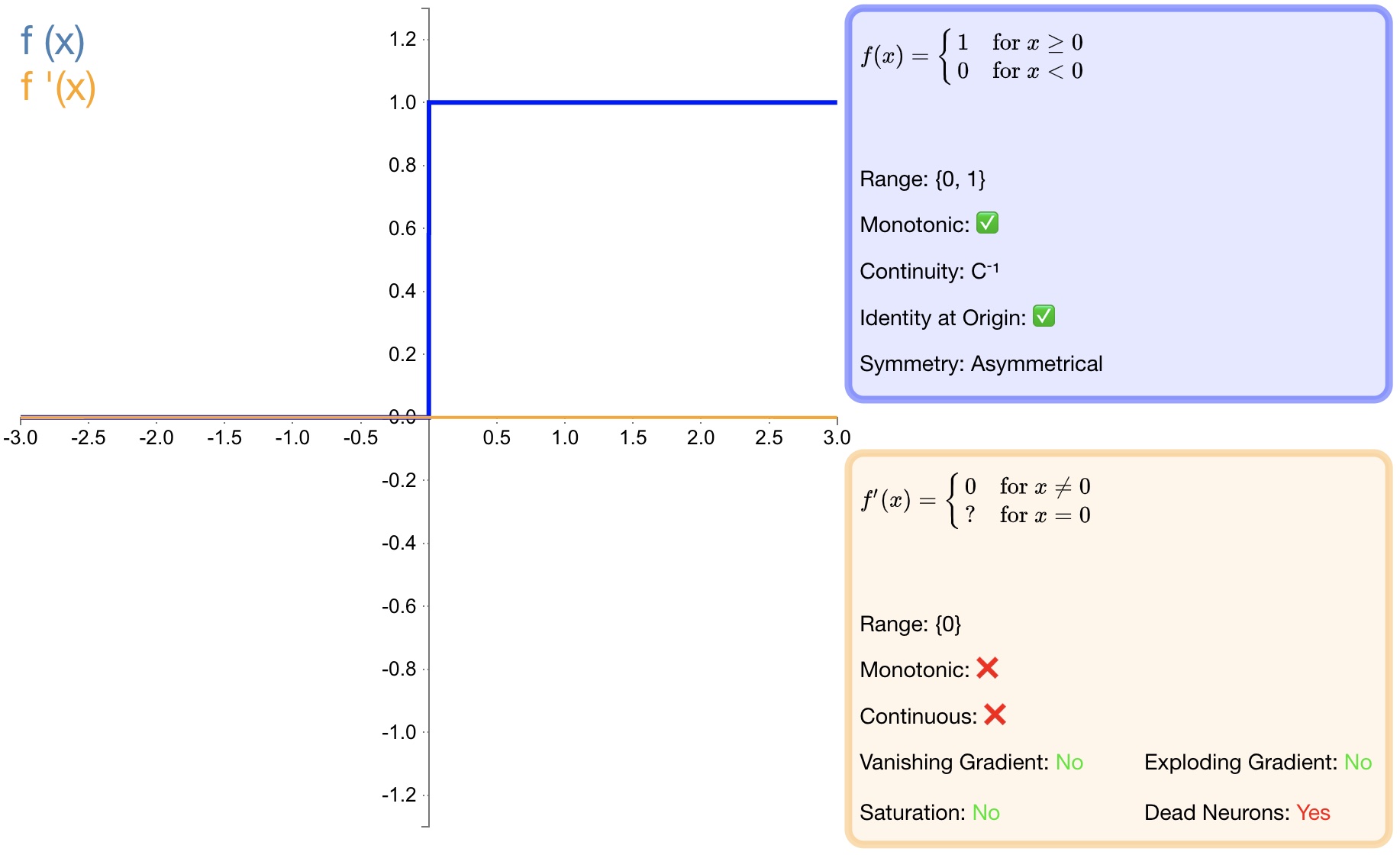
图2 step
优点:激活函数 $Step$ 更倾向于理论而不是实际,它模仿了生物神经元要么全有要么全无的属性。
缺点:它无法应用于神经网络因为其导数是 $0$(除了零点导数无定义以外),这意味着基于梯度的优化方法并不可行。
3.3. sigmoid
函数定义:
$${ f }(x)=\sigma (x)=\frac { 1 }{ 1+{ e }^{ -x } } $$
导数:
$${ f }^{ ' }(x)=f(x)(1-f(x))$$
函数图形如 图3 所示:
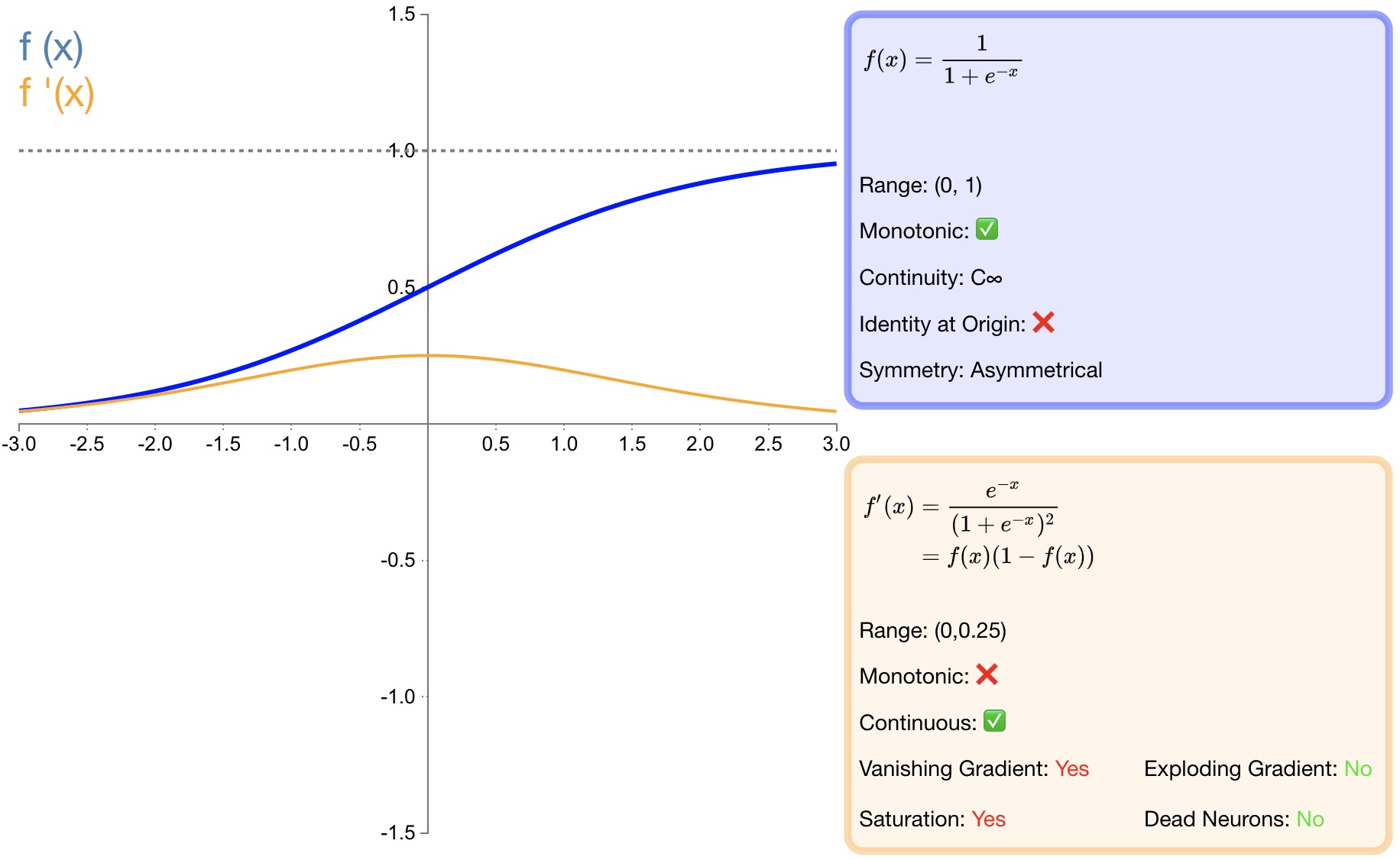
图3 sigmoid
优点:
[1] - $sigmoid$ 函数的输出映射在 $(0,1)$ 之间,单调连续,输出范围有限,优化稳定,可以用作输出层;
[2] - 求导容易;
缺点:
[1] - 由于其软饱和性,一旦落入饱和区梯度就会接近于0,根据反向传播的链式法则,容易产生梯度消失,导致训练出现问题;
[2] - 其输出并不是以 $0$ 为中心的,假设输入均为正数(或负数),那么对w的导数总是正数(或负数),这样在反向传播过程中要么都往正方向更新,要么都往负方向更新,导致有一种捆绑效果,使得收敛缓慢;
[3] - 计算时,由于具有幂运算,计算复杂度较高,运算速度较慢。
3.4. tanh
函数定义:
$${ f }(x)=tanh(x)=\frac { { e }^{ x }-{ e }^{ -x } }{ { e }^{ x }+{ e }^{ -x } }$$
导数:
$${ f }^{ ' }(x)=1-f(x)^{ 2 }$$
函数图形如 图4 所示:
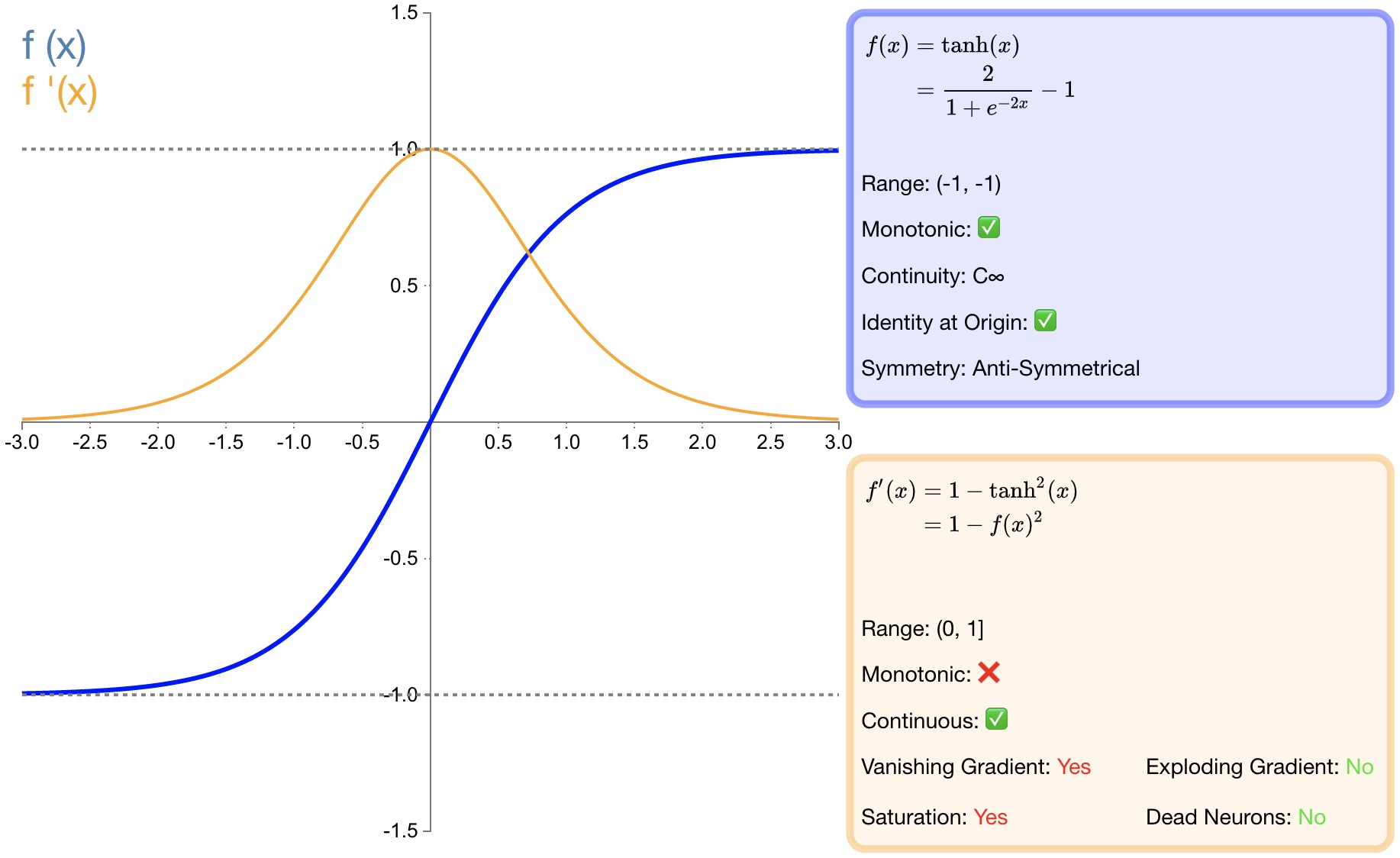
图4 tanh
优点:
[1] - $tanh$ 比 $sigmoid$ 函数收敛速度更快;
[2] - 相比 $sigmoid$ 函数,$tanh$ 是以 $0$ 为中心的;
缺点:
[1] - 与 $sigmoid$ 函数相同,由于饱和性容易产生的梯度消失;
[2] - 与 $sigmoid$ 函数相同,由于具有幂运算,计算复杂度较高,运算速度较慢。
3.5. ReLU
函数定义:
$$f(x)=\begin{cases} \begin{matrix} 0 & x<0 \end{matrix} \\ \begin{matrix} x & x\ge 0 \end{matrix} \end{cases}$$
导数:
$${ { f }(x) }^{ ' }=\begin{cases} \begin{matrix} 0 & x<0 \end{matrix} \\ \begin{matrix} 1 & x\ge 0 \end{matrix} \end{cases}$$
函数图如 图5 所示:
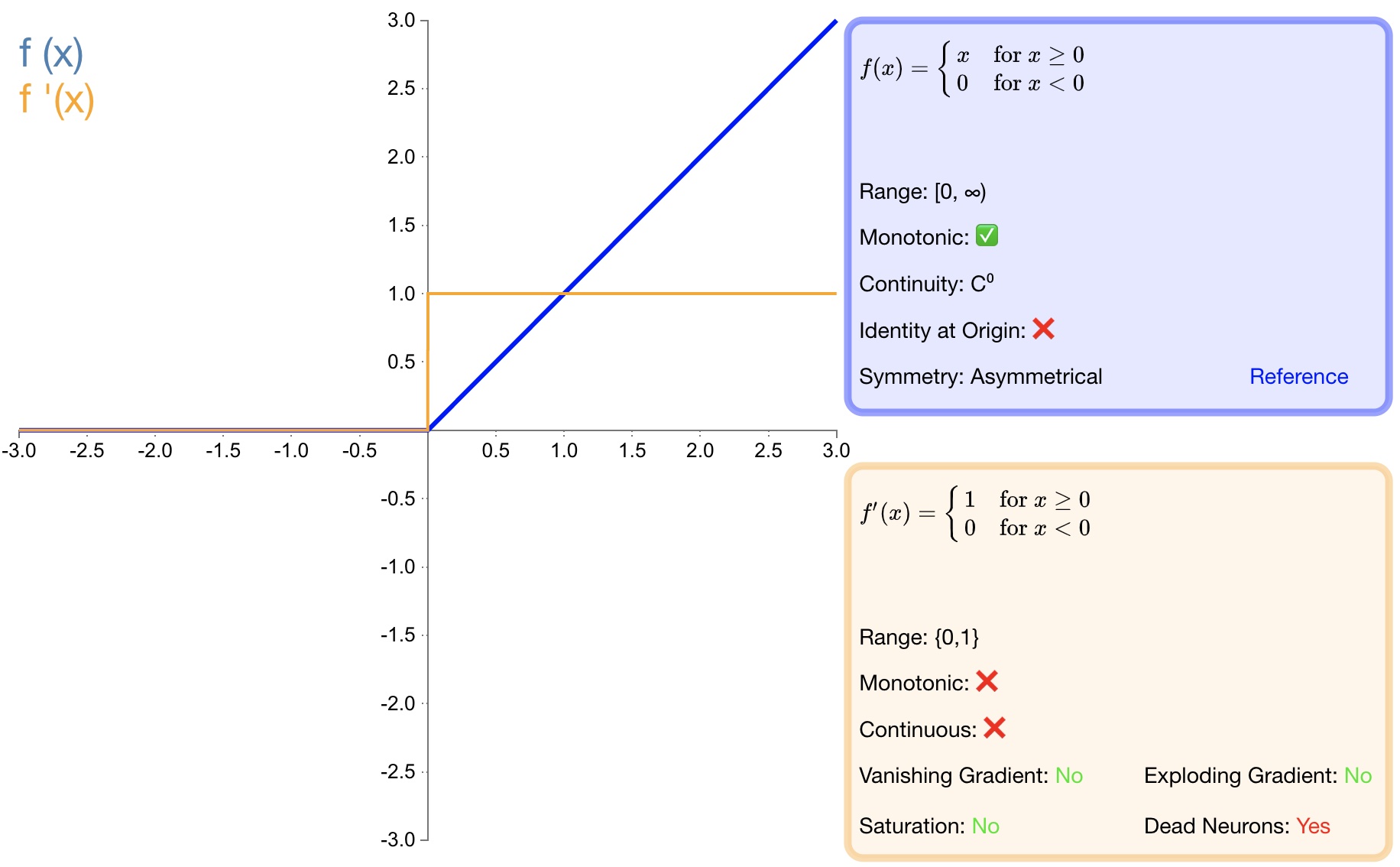
图5 ReLU
优点:
[1] - 收敛速度快;
[2] - 相较于 $sigmoid$ 和 $tanh$ 中涉及了幂运算,导致计算复杂度高, ReLU可以更加简单的实现;
[3] - 当输入 $x>=0$ 时,ReLU 的导数为常数,这样可有效缓解梯度消失问题;
[4] - 当 $x<0$ 时,ReLU 的梯度总是 $0$,提供了神经网络的稀疏表达能力;
缺点:
[1] - ReLU 的输出不是以 $0$ 为中心的;
[2] - 神经元坏死现象,某些神经元可能永远不会被激活,导致相应参数永远不会被更新;
[3] - 不能避免梯度爆炸问题;
3.6. LReLU
函数定义:
$$ f(x)=\begin{cases} \begin{matrix} \alpha x & x<0 \end{matrix} \\ \begin{matrix} x & x\ge 0 \end{matrix} \end{cases}$$
导数:
$${ { f }(x) }^{ ' }=\begin{cases} \begin{matrix} \alpha & x<0 \end{matrix} \\ \begin{matrix} 1 & x\ge 0 \end{matrix} \end{cases}$$
其中,$\alpha$ 常设置为0.01。函数图如 图6 所示:
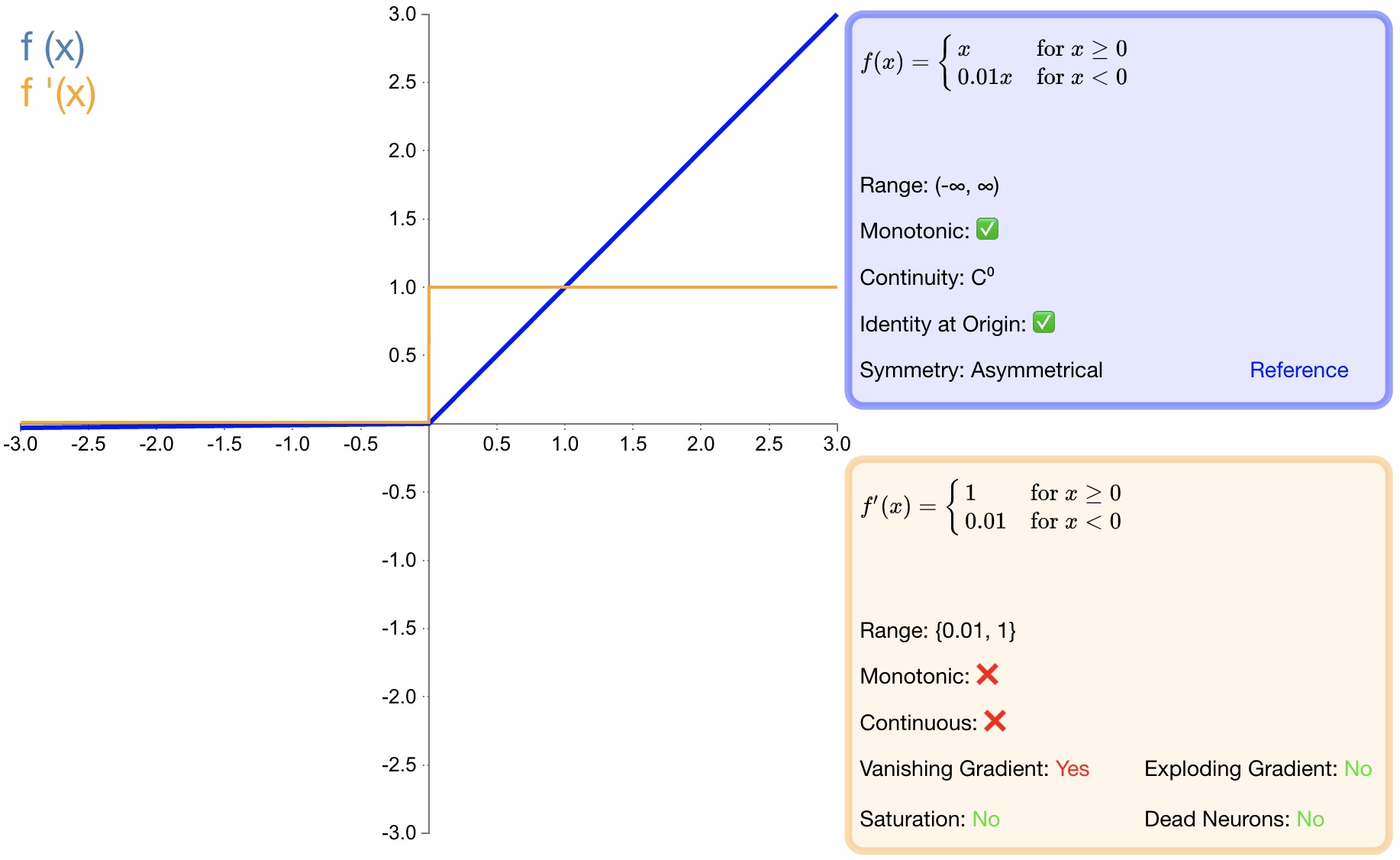
图6 LReLU
优点:
[1] - 避免梯度消失;
[2] - 由于导数总是不为零,因此可减少死神经元的出现;
缺点:
[1] - LReLU 表现并不一定比 ReLU 好;
[2] - 无法避免梯度爆炸问题;
3.7. PReLU
函数定义:
$$f(\alpha ,x)=\begin{cases} \begin{matrix} \alpha x & x<0 \end{matrix} \\ \begin{matrix} x & x\ge 0 \end{matrix} \end{cases}$$
导数:
$${ { f }(\alpha ,x) }^{ ' }=\begin{cases} \begin{matrix} \alpha & x<0 \end{matrix} \\ \begin{matrix} 1 & x\ge 0 \end{matrix} \end{cases}$$
函数图如 图7 所示:
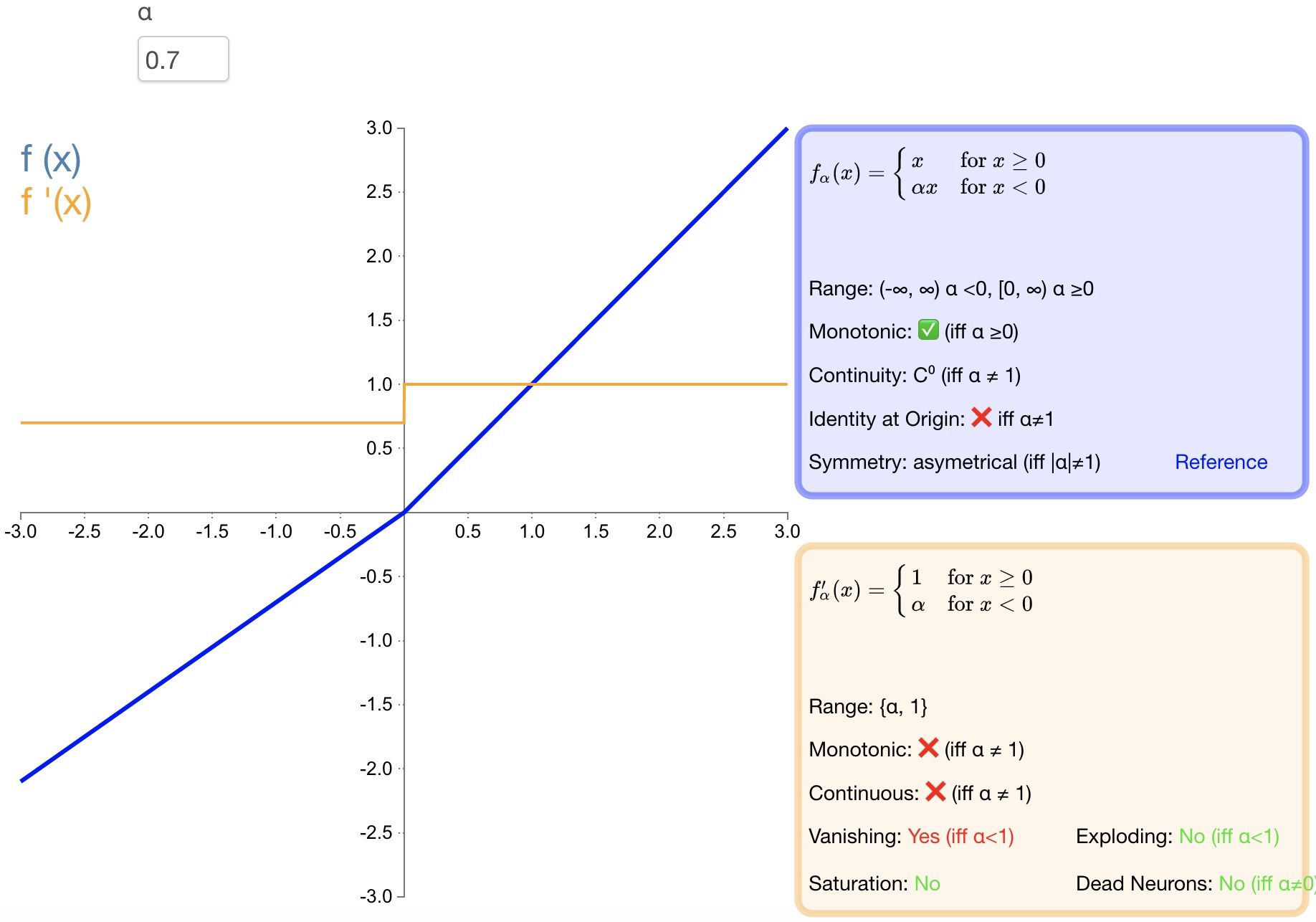
图7 PReLU
优点:
[1] - PReLU 是 LReLU 的改进,可以自适应地从数据中学习参数;
[2] - 收敛速度快、错误率低;
[3] - PReLU 可以用于反向传播的训练,可以与其他层同时优化;
3.8. RReLU
函数定义:
$$f(\alpha ,x)=\begin{cases} \begin{matrix} \alpha x & x<0 \end{matrix} \\ \begin{matrix} x & x\ge 0 \end{matrix} \end{cases}$$
导数:
$${ { f }(\alpha ,x) }^{ ' }=\begin{cases} \begin{matrix} \alpha & x<0 \end{matrix} \\ \begin{matrix} 1 & x\ge 0 \end{matrix} \end{cases}$$
函数图形如 图8 所示:
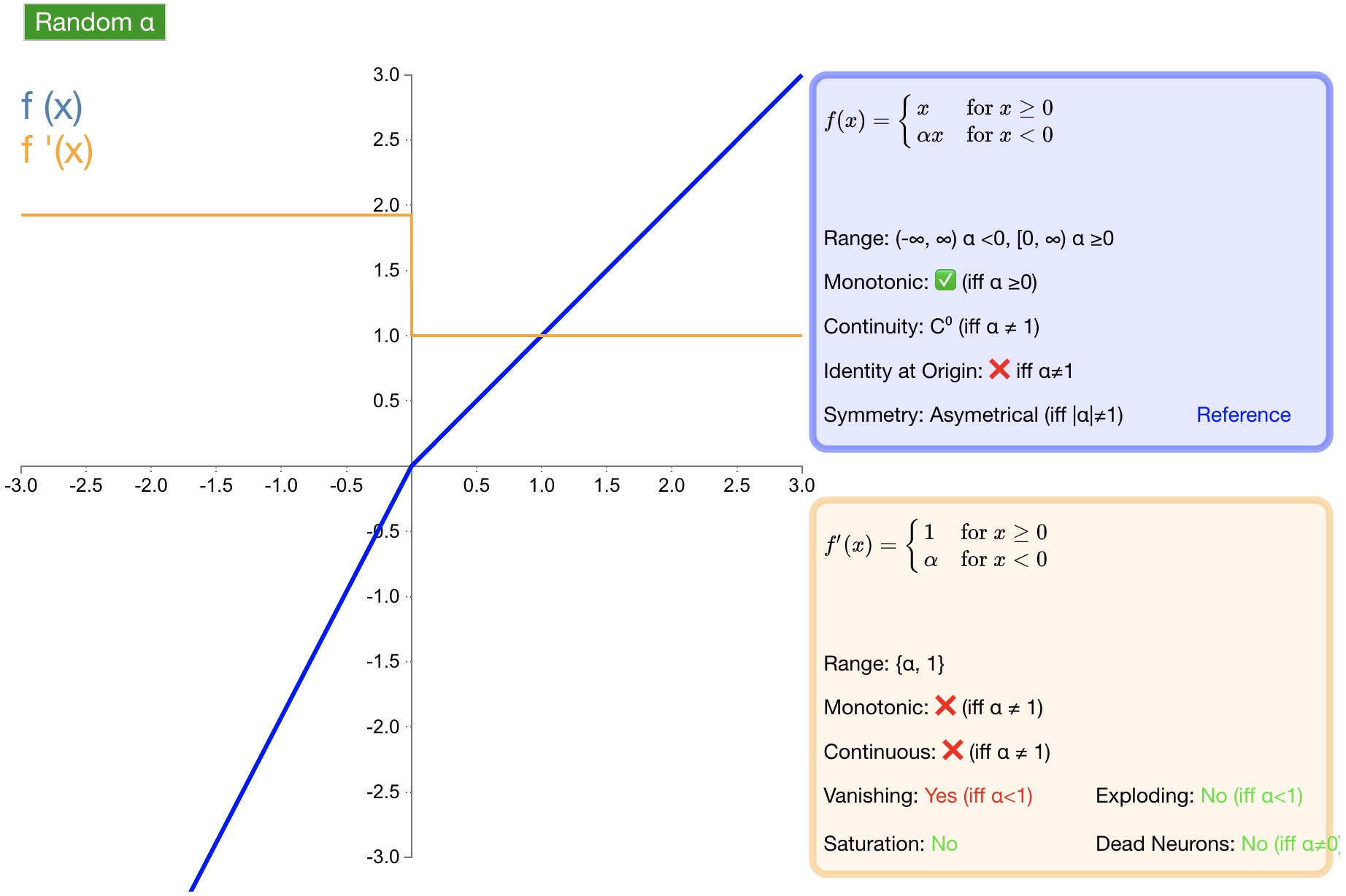
图8 RReLU
优点:为负值输入添加了一个线性项,这个线性项的斜率在每一个节点上都是随机分配的(通常服从均匀分布)。
3.9. ELU
函数定义:
$$ f(\alpha ,x)=\begin{cases} \begin{matrix} \alpha \left( { e }^{ x }-1 \right) & x<0 \end{matrix} \\ \begin{matrix} x & x\ge 0 \end{matrix} \end{cases}$$
导数:
$${ { f }(\alpha ,x) }^{ ' }=\begin{cases} \begin{matrix} f(\alpha ,x)+\alpha & x<0 \end{matrix} \\ \begin{matrix} 1 & x\ge 0 \end{matrix} \end{cases}$$
函数图形如 图9 所示:

图9 ELU
优点:
[1] - 导数收敛为零,从而提高学习效率;
[2] - 能得到负值输出,这能帮助网络向正确的方向推动权重和偏置变化;
[3] - 防止死神经元出现。
缺点:
[1] - 计算量大,其表现并不一定比 ReLU 好;
[2] - 无法避免梯度爆炸问题;
3.10. SELU
函数定义:
$$f(\alpha ,x)=\lambda \begin{cases} \begin{matrix} \alpha \left( { e }^{ x }-1 \right) & x<0 \end{matrix} \\ \begin{matrix} x & x\ge 0 \end{matrix} \end{cases}$$
导数:
$${ { f }(\alpha ,x) }^{ ' }=\lambda \begin{cases} \begin{matrix} \alpha \left( { e }^{ x } \right) & x<0 \end{matrix} \\ \begin{matrix} 1 & x\ge 0 \end{matrix} \end{cases}$$
函数图形 如图10 所示:

图10 SELU
优点:
[1] - SELU 是 ELU 的一个变种。其中 λ 和 α 是固定数值(分别为 $1.0507$ 和 $1.6726$);
[2] - 经过该激活函数后使得样本分布自动归一化到 $0$ 均值和单位方差;
[3] - 不会出现梯度消失或爆炸问题;
3.11. softsign
函数定义:
$$f(x)=\frac { x }{ \left| x \right| +1 }$$
导数:
$${ f }^{ ' }(x)=\frac { 1 }{ { (1+\left| x \right| ) }^{ 2 } } $$
函数图形如 图 11 所示:

图11 softsign
优点:
[1] - $softsign$ 是 $tanh$ 激活函数的另一个替代选择;
[2] - $softsign$ 是反对称、去中心、可微分,并返回 $-1$ 和 $1$ 之间的值;
[3] - $softsign$ 更平坦的曲线与更慢的下降导数表明它可以更高效地学习;
缺点:
[1] - 导数的计算比$tanh$ 更麻烦;
3.12. softplus
函数定义:
$$f(x)=\ln { (1+{ e }^{ x }) }$$
导数:
$${ f }^{ ' }(x)=\frac { 1 }{ 1+{ e }^{ -x } }$$
函数图形如 图12 所示:
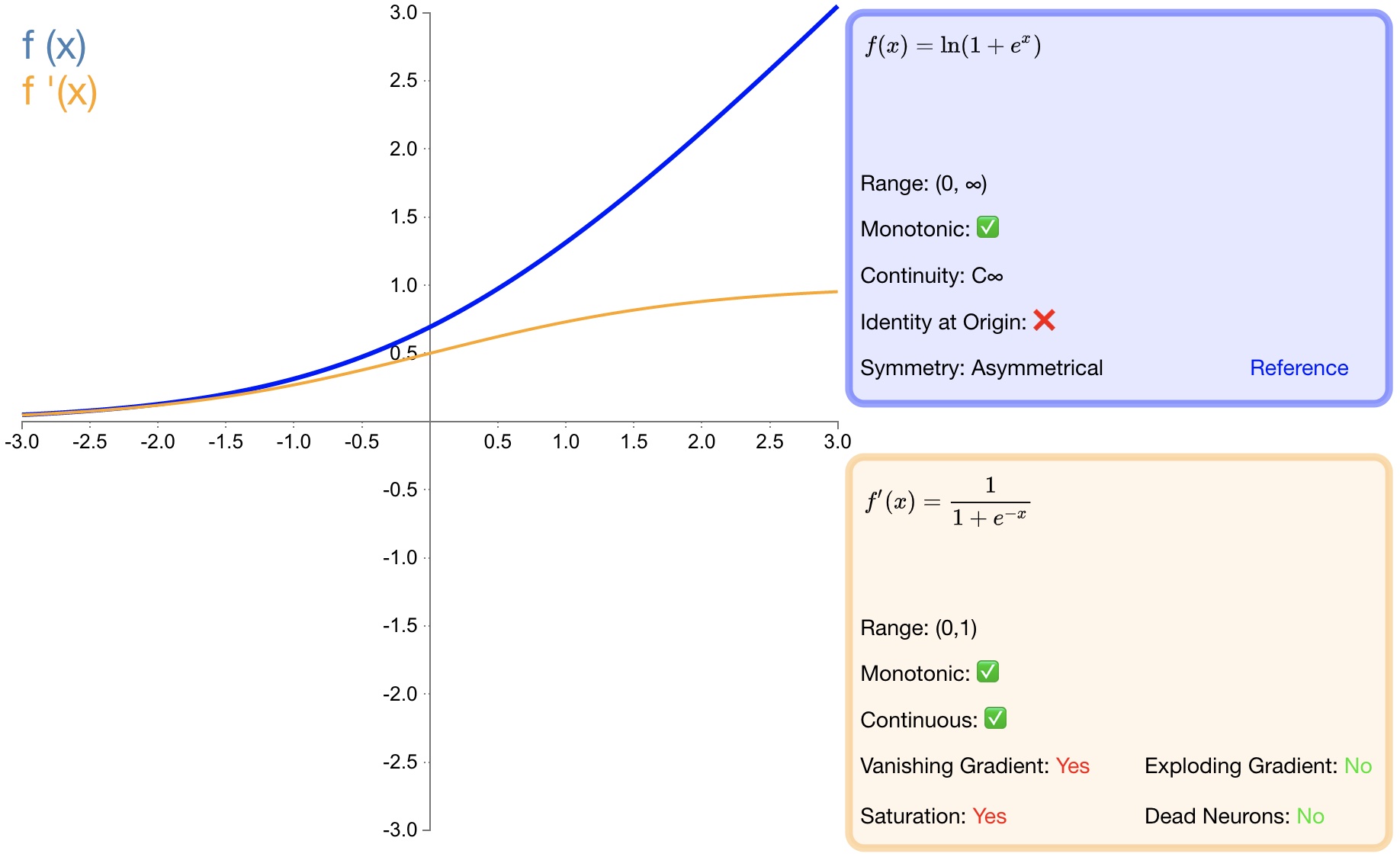
图12 softplus
优点:
[1] - 作为 $relu$ 的一个不错的替代选择,$softplus$ 能够返回任何大于 $0$ 的值。
[2] - 与 $relu$ 不同,$softplus$ 的导数是连续的、非零的,无处不在,从而防止出现死神经元。
缺点:
[1] - 导数常常小于 $1$ ,也可能出现梯度消失的问题。
[2] - $softplus$ 另一个不同于 $relu$ 的地方在于其不对称性,不以零为中心,可能会妨碍学习。
3.13. softmax
softmax 函数一般用于多分类问题中,它是对逻辑斯蒂(logistic)回归的一种推广,也被称为多项逻辑斯蒂回归模型(multi-nominal logistic mode)。假设要实现 k 个类别的分类任务,Softmax 函数将输入数据 $x_i$ 映射到第 $i$ 个类别的概率 $y_i$ 如下计算:
$$ y_i=soft\max \left( x_i \right) =\frac{e^{x_i}}{\sum_{j=1}^k{e^{x_j}}} $$
显然,$0<y_i<1$。图13 给出了三类分类问题的 softmax 输出示意图。在图中,对于取值为 4、1和-4 的 $x_1$、$x_2$ 和 $x_3$,通过 softmax 变换后,将其映射到 (0,1) 之间的概率值。
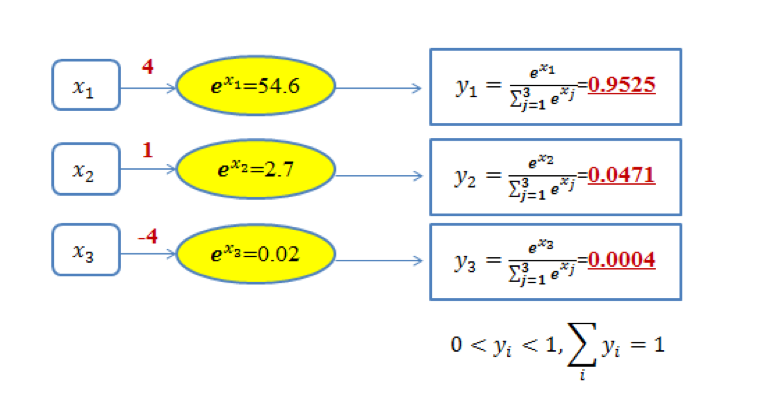
图13 三类分类问题的softmax输出示意图
由于 softmax 输出结果的值累加起来为 1,因此可将输出概率最大的作为分类目标(图 1 中被分类为第一类)。
也可以从如下另外一个角度来理解图 1 中的内容:给定某个输入数据,可得到其分类为三个类别的初始结果,分别用 $x_1$、$x_2$ 和 $x_3$ 来表示。这三个初始分类结果分别是 4、1和-4。通过 Softmax 函数,得到了三个类别分类任务中以概率表示的更好的分类结果,即分别以 95.25%、4.71%和0.04% 归属于类别1、类别2 和类别3。显然,基于这样的概率值,可判断输入数据属于第一类。可见,通过使用 Softmax 函数,可求取输入数据在所有类别上的概率分布。
3.14. swish
函数定义:
$$f\left( x \right) =x\cdot \sigma \left( x \right) $$
其中,$\sigma$ 是 $sigmoid$ 函数。
$swish$ 激活函数的图形如 图14 所示:
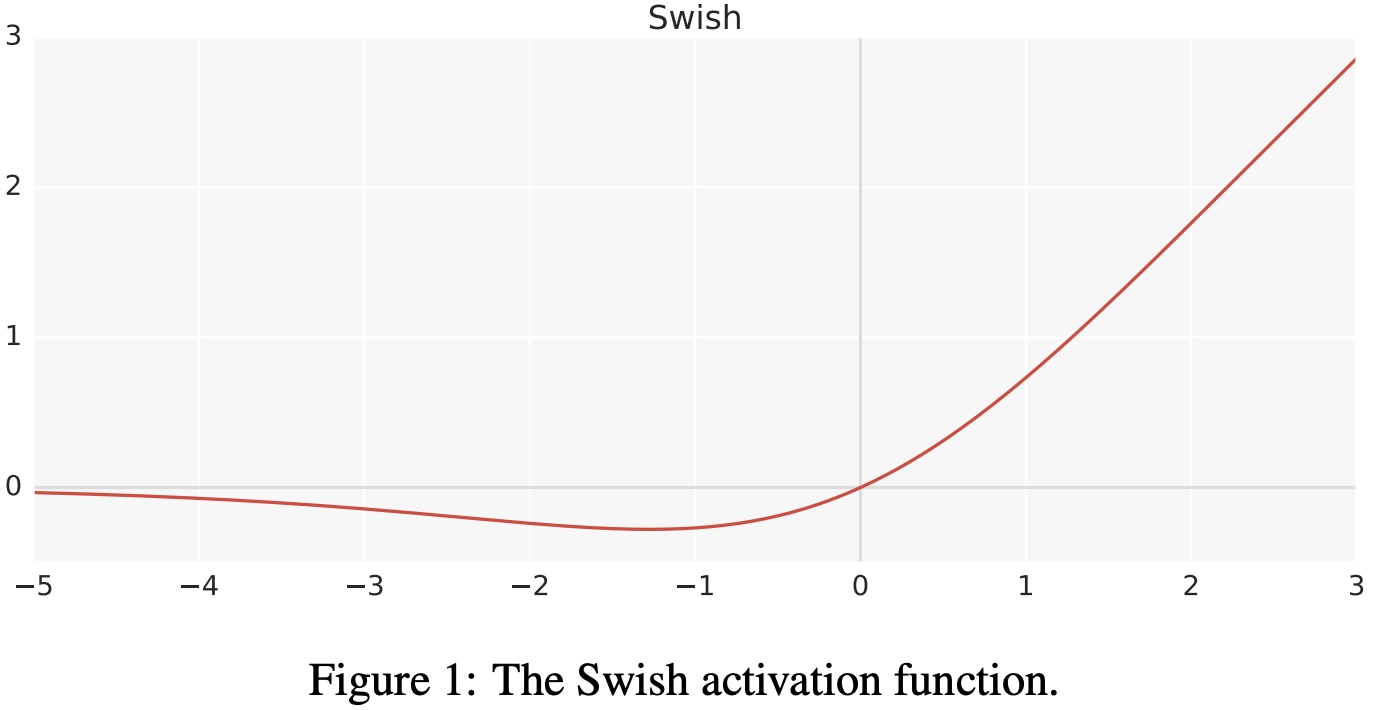
图14 swish 激活函数
$swish$ 激活函数的一阶导数如下:
$$ f^{'}\left( x \right) =\sigma \left( x \right) +x\cdot \sigma \left( x \right) \left( 1-\sigma \left( x \right) \right) $$
$$ f^{'}\left( x \right) = \sigma \left( x \right) +x\cdot \sigma \left( x \right) -x\cdot \sigma \left( x \right) ^2\\ $$
$$ f^{'}\left( x \right) = x\cdot \sigma \left( x \right) +\sigma \left( x \right) \left( 1-x\cdot \sigma \left( x \right) \right) $$
$$ f^{'}\left( x \right) =f\left( x \right) +\sigma \left( x \right) \left( 1-f\left( x \right) \right) $$
$swish$ 激活函数的一阶和二阶导数的图形如 图15 所示:
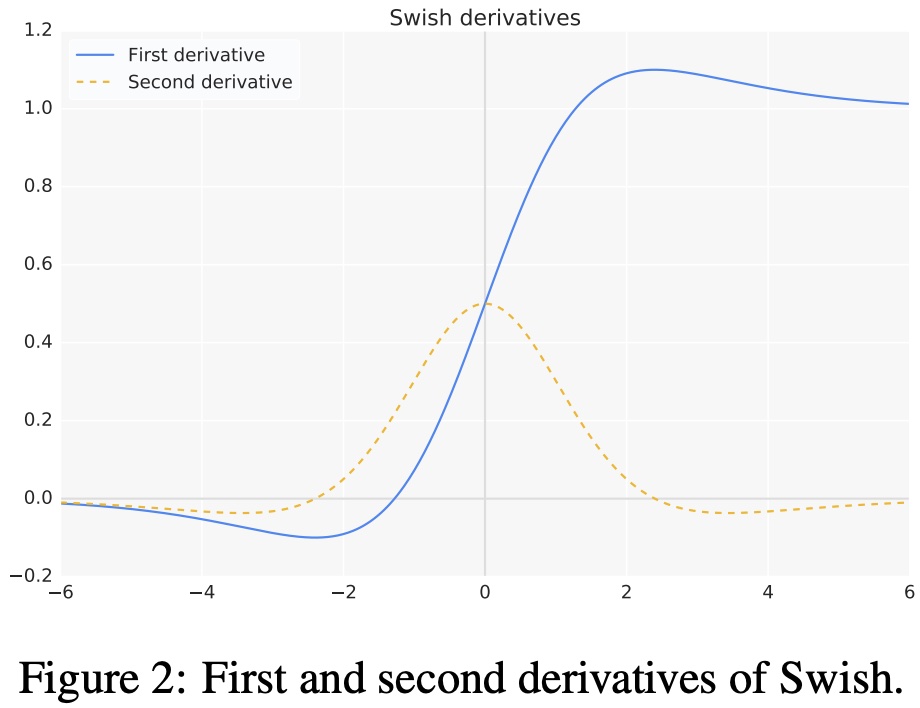
图15 swish 导数
超参数版 $swish$ 激活函数:
$$f\left( x \right) =x\cdot \sigma \left( \beta x \right)$$
其中,$\beta$ 是超参数。超参数版 $swish$ 激活函数的图形如 图16 所示:
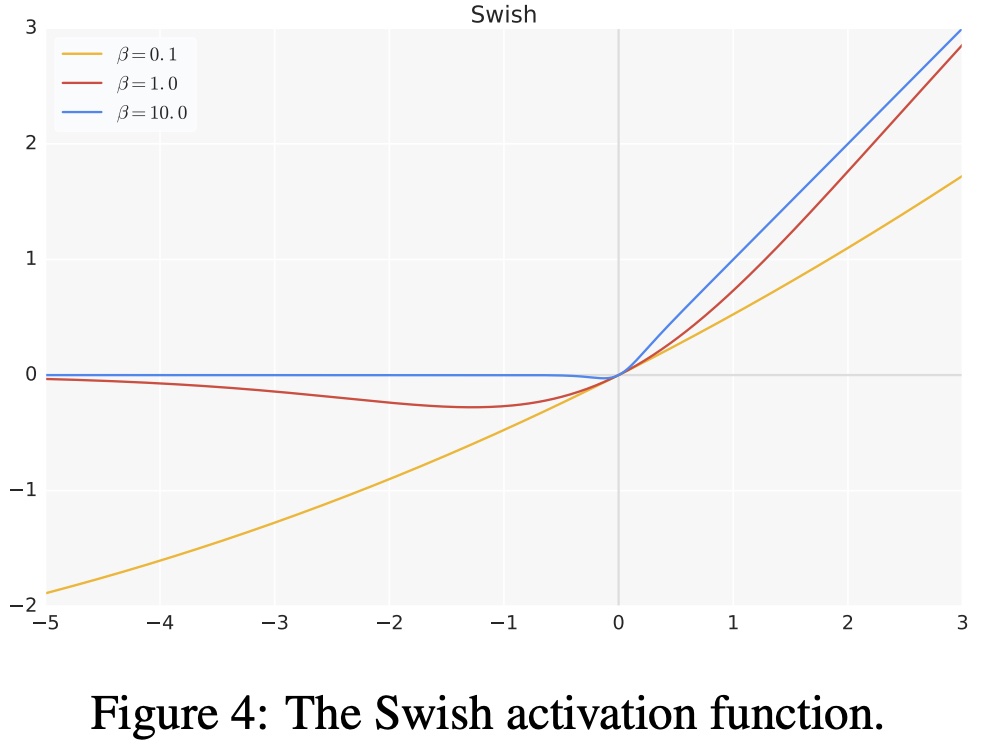
图16 swish 超参数
优点:
[1] - 当 $x>0$ 时,不存在梯度消失的情况;当 $x<0$ 时,神经元也不会像 ReLU 一样出现死亡的情况;
[2] - $swish$ 处处可导,连续光滑;
[3] - $swish$ 并非一个单调的函数;
[4] - 提升了模型的性能;
缺点:
[1] - 计算量大;
3.15. hswish
函数定义:
$$f\left( x \right) =x\frac{\text{Re}LU6\left( x+3 \right)}{6}$$
$hard \ swish$ 和 $swish$ 激活函数对比如 图17 所示:
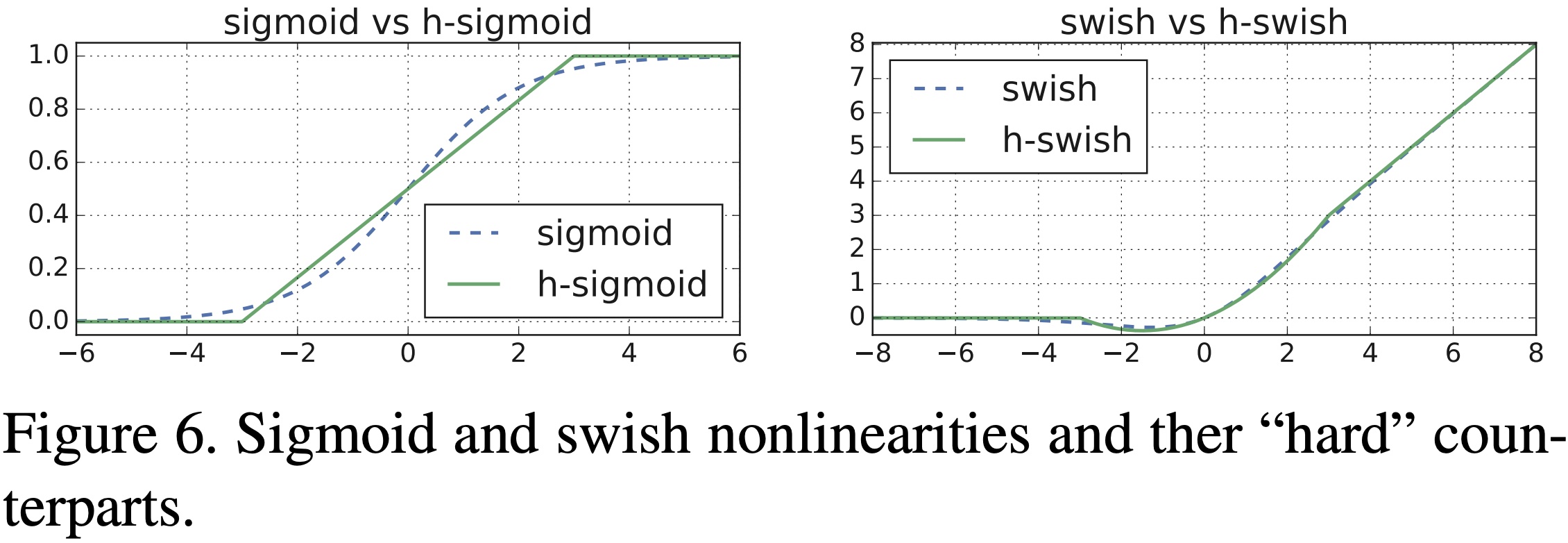
图17 Hard Swish
优点:
[1] - 与 $swish$ 相比 $hard \ swish$ 减少了计算量,具有和 $swish$ 同样的性质。
缺点:
[1] - 与 $relu6$ 相比 $hard \ swish$ 的计算量仍然较大。
4. 激活函数的选择
[1] - 浅层网络在分类器时,$sigmoid$ 函数及其组合通常效果更好。
[2] - 由于梯度消失问题,有时要避免使用 $sigmoid$ 和 $tanh$ 函数。
[3] - $relu$ 函数是一个通用的激活函数,目前在大多数情况下使用。
[4] - 如果神经网络中出现死神经元,那么 $prelu$ 函数就是最好的选择。
[5] - $relu$ 函数只能在隐藏层中使用。
[6] - 通常,可以从 $relu$ 函数开始,如果 $relu$ 函数没有提供最优结果,再尝试其他激活函数。
5. 激活函数相关问题
5.1. 为什么 $relu$ 不是全程可微/可导也能用于基于梯度的学习?
从数学的角度看 $relu$ 在 $0$ 点不可导,因为它的左导数和右导数不相等;但在实现时通常会返回左导数或右导数的其中一个,而不是报告一个导数不存在的错误,从而避免了这个问题。
5.2. 为什么 $tanh$ 的收敛速度比 $sigmoid$ 快?
$$\tan\text{h}^{'}\left( x \right) =1-\tan\text{h}\left( x \right) ^2\in \left( 0,1 \right) $$
$$s^{'}\left( x \right) =s\left( x \right) \left( 1-s\left( x \right) \right) \in \left( 0,\frac{1}{4} \right] $$
由上面两个公式可知 $tanh$ 引起的梯度消失问题没有 $sigmoid$ 严重,所以 $tanh$ 收敛速度比 $sigmoid$ 快。
5.3. sigmoid 和 softmax 有什么区别?
[1] - 二分类问题时 $sigmoid$ 和 $softmax$ 是一样的,都是求 $cross \ entropy \ loss$ ,而 $softmax$ 可以用于多分类问题。
[2] - $softmax$ 是 $sigmoid$ 的扩展,因为,当类别数 $k=2$ 时,$softmax$ 回归退化为 $logistic$ 回归。
[3] - $softmax$ 建模使用的分布是多项式分布,而 $logistic$ 则基于伯努利分布。
[4] - 多个 $logistic$ 回归通过叠加也同样可以实现多分类的效果,但是 $softmax$ 回归进行的多分类,类与类之间是互斥的,即一个输入只能被归为一类;多 $logistic$ 回归进行多分类,输出的类别并不是互斥的,即"苹果"这个词语既属于"水果"类也属于"$3C$"类别。