超像素分割,SLIC,Simple Linear Iterative Clustering,是一种迭代聚类算法. 出自 PAMI2012 论文 SLIC Superpixels Compared to State-of-the-art Superpixel Methods.
1. SLIC 算法流程
SLIC 算法流程如:

其中,主要有如下几个关键点:
[1] - 初始化图像分割块:
每个分割的图像块都是一个聚类,聚类中心称之为 superpixel,类似于 Kmeans 算法,需要手工指定聚类个数.
SLIC 算法首先将原始图像分割大小一致的图像 patch,假设图像的像素个数为 $N$,待分割的图像 patch 个数为 $k$,每个图像 patch 大小为 $ S \times S$,其中 $S = \sqrt{N/k}$.
[2] - 初始化图像块的聚类中心
对于分割后的图像块,随机采样一个像素点作为聚类中心 $C_k$.
此处,为了避免初始的采样点出现在噪声或边缘部分,采取的方式是,在采样点附近 3x3 的区域,计算临近像素点的梯度,并将临近点中梯度最小的点作为聚类中心.
[3] - 计算各像素点与聚类中心的距离
对于图像块以及对应的聚类中心,如果根据一般聚类算法,如 Kmeans 等,往往是计算每个像素点和聚类中心的距离. 显然,每个聚类中心都要和所有的图像像素点计算距离,是比较费时的.
而,SLIC 算法采用的策略是,只计算每个聚类中心周围 $2S \times 2S$ 范围内的像素点与该聚类中心的距离,可以节省很多计算量.
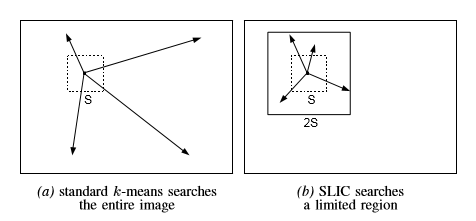
SLIC 同时考虑了空间距离和颜色距离,
$$ d_c = \sqrt{(l_j - l_i)^2 + (a_j - a_i)^2 + (b_j- b_i)^2} $$
$$ d_s = \sqrt{(x_j - x_i)^2 + (y_j - y_i)^2} $$
$$ D = \sqrt{(d_c)^2 + (\frac{d_s}{S})^2 m^2} $$
其中,论文中提到,CIELAB 空间中 $m$ 取值范围大概为 [1, 40].
[4] - 重新聚类
根据计算后的聚类,更新每个像素点所属于的图像块; 然后,将同一个图像块的像素点求平均,得到新的图像块聚类中心.
重复以上步骤,直到两次聚类中心的聚类小于某个阈值.
2. SLIC 示例
基于 scikit-image 中 skimage.segmentation.slic 的实现如下:
from skimage.segmentation import slic
from skimage.segmentation import mark_boundaries
from skimage.util import img_as_float
from skimage import io
import matplotlib.pyplot as plt
#加载图片
image = img_as_float(io.imread("image.jpg"))
#
for numSegments in (100, 200, 300):
#SLIC
segments = slic(image, n_segments = numSegments, sigma = 5)
# show the output of SLIC
fig = plt.figure("Superpixels -- %d segments" % (numSegments))
ax = fig.add_subplot(1, 1, 1)
ax.imshow(mark_boundaries(image, segments))
plt.axis("off")
# show the plots
plt.show()3. skimage.segmentation.slic 函数
skimage.segmentation.slic 函数定义如:
skimage.segmentation.slic(
image,
n_segments=100, #分割输出的标签数
compactness=10.0, #平衡颜色优先性和空间优先性. 值越大,空间优先性权重越大
max_iter=10, #Kmeans 最大迭代数
sigma=0, #图像每一维预处理的高斯核宽度
spacing=None, #
multichannel=True,
convert2lab=None,
enforce_connectivity=True,
min_size_factor=0.5,
max_size_factor=3,
slic_zero=False,
start_label=None,
mask=None)注:
[1] - 如果 sigma > 0,则在分割前,先采用高斯核平滑图像.
[2] - 如果 sigma 是标量,且提供了 spacing 参数,则,高斯核宽度会根据 spacing 对每一维进行划分. 例如,如果 sigma=1,spacing=[5, 1, 1],则有效的 sigma 是 [0.2, 1, 1]. (有助于确保 anisotropic 图像的合理平滑.)
[3] - 处理前,图像像素值被缩放到 [0, 1].
[4] - 默认是 (M, N, 3) 的2D RGB 图像.
4. skimage.segmentation.slic 源码
https://github.com/scikit-image/scikit-image/blob/main/skimage/segmentation/slic_superpixels.py
import warnings
from collections.abc import Iterable
import numpy as np
from scipy import ndimage as ndi
from scipy.spatial.distance import pdist, squareform
from scipy.cluster.vq import kmeans2
from numpy import random
from ._slic import (_slic_cython, _enforce_label_connectivity_cython)
from ..util import img_as_float, regular_grid
from ..color import rgb2lab
def _get_mask_centroids(mask, n_centroids, multichannel):
"""
Find regularly spaced centroids on a mask.
"""
# Get tight ROI around the mask to optimize
coord = np.array(np.nonzero(mask), dtype=float).T
# Fix random seed to ensure repeatability
rnd = random.RandomState(123)
# select n_centroids randomly distributed points from within the mask
idx_full = np.arange(len(coord), dtype=int)
idx = np.sort(
rnd.choice(idx_full, min(n_centroids, len(coord)),
replace=False))
# To save time, when n_centroids << len(coords), use only a subset of the
# coordinates when calling k-means. Rather than the full set of coords,
# we will use a substantially larger subset than n_centroids. Here we
# somewhat arbitrarily choose dense_factor=10 to make the samples
# 10 times closer together along each axis than the n_centroids samples.
dense_factor = 10
ndim_spatial = mask.ndim - 1 if multichannel else mask.ndim
n_dense = int((dense_factor ** ndim_spatial) * n_centroids)
if len(coord) > n_dense:
# subset of points to use for the k-means calculation
# (much denser than idx, but less than the full set)
idx_dense = np.sort(
rnd.choice(idx_full, n_dense, replace=False))
else:
idx_dense = Ellipsis
centroids, _ = kmeans2(coord[idx_dense], coord[idx], iter=5)
# Compute the minimum distance of each centroid to the others
dist = squareform(pdist(centroids))
np.fill_diagonal(dist, np.inf)
closest_pts = dist.argmin(-1)
steps = abs(centroids - centroids[closest_pts, :]).mean(0)
return centroids, steps
def _get_grid_centroids(image, n_centroids):
"""
Find regularly spaced centroids on the image.
"""
d, h, w = image.shape[:3]
grid_z, grid_y, grid_x = np.mgrid[:d, :h, :w]
slices = regular_grid(image.shape[:3], n_centroids)
centroids_z = grid_z[slices].ravel()[..., np.newaxis]
centroids_y = grid_y[slices].ravel()[..., np.newaxis]
centroids_x = grid_x[slices].ravel()[..., np.newaxis]
centroids = np.concatenate([centroids_z, centroids_y, centroids_x],
axis=-1)
steps = np.asarray([float(s.step) if s.step is not None else 1.0
for s in slices])
return centroids, steps
def slic(image, n_segments=100, compactness=10., max_iter=10, sigma=0,
spacing=None, multichannel=True, convert2lab=None,
enforce_connectivity=True, min_size_factor=0.5, max_size_factor=3,
slic_zero=False, start_label=None, mask=None):
"""
Segments image using k-means clustering in Color-(x,y,z) space.
"""
image = img_as_float(image)
use_mask = mask is not None
dtype = image.dtype
is_2d = False
if image.ndim == 2:
# 2D grayscale image
image = image[np.newaxis, ..., np.newaxis]
is_2d = True
elif image.ndim == 3 and multichannel:
# Make 2D multichannel image 3D with depth = 1
image = image[np.newaxis, ...]
is_2d = True
elif image.ndim == 3 and not multichannel:
# Add channel as single last dimension
image = image[..., np.newaxis]
if multichannel and (convert2lab or convert2lab is None):
if image.shape[-1] != 3 and convert2lab:
raise ValueError("Lab colorspace conversion requires a RGB image.")
elif image.shape[-1] == 3:
image = rgb2lab(image)
if start_label is None:
if use_mask:
start_label = 1
else:
warnings.warn("skimage.measure.label's indexing starts from 0. " +
"In future version it will start from 1. " +
"To disable this warning, explicitely " +
"set the `start_label` parameter to 1.",
FutureWarning, stacklevel=2)
start_label = 0
if start_label not in [0, 1]:
raise ValueError("start_label should be 0 or 1.")
# initialize cluster centroids for desired number of segments
update_centroids = False
if use_mask:
mask = np.ascontiguousarray(mask, dtype=bool).view('uint8')
if mask.ndim == 2:
mask = np.ascontiguousarray(mask[np.newaxis, ...])
if mask.shape != image.shape[:3]:
raise ValueError("image and mask should have the same shape.")
centroids, steps = _get_mask_centroids(mask, n_segments, multichannel)
update_centroids = True
else:
centroids, steps = _get_grid_centroids(image, n_segments)
if spacing is None:
spacing = np.ones(3, dtype=dtype)
elif isinstance(spacing, (list, tuple)):
spacing = np.ascontiguousarray(spacing, dtype=dtype)
if not isinstance(sigma, Iterable):
sigma = np.array([sigma, sigma, sigma], dtype=dtype)
sigma /= spacing.astype(dtype)
elif isinstance(sigma, (list, tuple)):
sigma = np.array(sigma, dtype=dtype)
if (sigma > 0).any():
# add zero smoothing for multichannel dimension
sigma = list(sigma) + [0]
image = ndi.gaussian_filter(image, sigma)
n_centroids = centroids.shape[0]
segments = np.ascontiguousarray(np.concatenate(
[centroids, np.zeros((n_centroids, image.shape[3]))],
axis=-1), dtype=dtype)
# Scaling of ratio in the same way as in the SLIC paper so the
# values have the same meaning
step = max(steps)
ratio = 1.0 / compactness
image = np.ascontiguousarray(image * ratio, dtype=dtype)
if update_centroids:
# Step 2 of the algorithm [3]_
_slic_cython(image, mask, segments, step, max_iter, spacing,
slic_zero, ignore_color=True,
start_label=start_label)
labels = _slic_cython(image, mask, segments, step, max_iter,
spacing, slic_zero, ignore_color=False,
start_label=start_label)
if enforce_connectivity:
if use_mask:
segment_size = mask.sum() / n_centroids
else:
segment_size = np.prod(image.shape[:3]) / n_centroids
min_size = int(min_size_factor * segment_size)
max_size = int(max_size_factor * segment_size)
labels = _enforce_label_connectivity_cython(
labels, min_size, max_size, start_label=start_label)
if is_2d:
labels = labels[0]
return labels5. 参考
[1] - 机器学习:simple linear iterative clustering (SLIC) 算法 - 2017.12.04
[2] - 计算 SLIC 超像素分割的邻接矩阵 - 2020.04.02
[3] - 【PYTHON】超像素分段【SLIC(SIMPLE LINEAR ITERATIVE CLUSTERING)简单的线性迭代聚类】