原文1：Implementing the five most popular Similarity Measures in Python - 2015.06.06

原文2：常用的相似度计算方法原理及实现 - 2017.04.11

在数据分析和数据挖掘等应用场景中，通常需要知道个体间差异的大小，进而评价个体的相似性和类别. 常见的比如数据分析中比如相关分析，数据挖掘中的分类聚类(K-Means等)算法，物品推荐时.

相似度就是比较两个事物的相似性. 一般通过计算事物的特征之间的距离，如果距离小，那么相似度大；如果距离大，那么相似度小. 比如两种水果，将从颜色，大小，维生素含量等特征进行比较相似性.

问题定义：有两个特征 向量 X, Y, 其都是 N 维特征，$X=(x_1, x_2, ..., x_n)$, $Y=(y_1, y_2, ..., y_n)$, 计算X 和 Y 的相似性. 相似性取值一般是在[0, 1]范围内. 如果 $X=Y$，则相似性值为 1，如果$X \neq Y$，则相似性值为0.

常用相似性距离计算有如下方法.

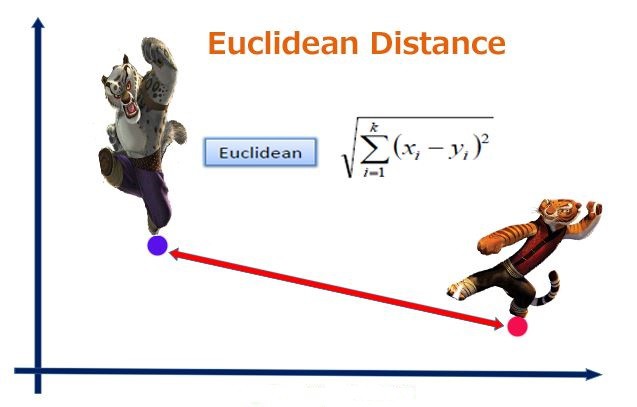
1. 欧式距离(Eucledian Distance)

欧氏距离是最常用的距离计算公式，衡量的是多维空间中各个点之间的绝对距离. 当数据很稠密并且连续时，其是一种很好的计算方式.

因为计算是基于各维度特征的绝对数值，所以欧氏度量需要保证各维度指标在相同的刻度级别，比如对身高(cm)和体重(kg)两个单位不同的指标使用欧式距离可能使结果失效.

实现：

from math import *

def euclidean_dist(x, y):
    return sqrt(sum(pow(a-b, 2) for a, b in zip(x, y)))

2. 曼哈顿距离(Manhatten Distance)

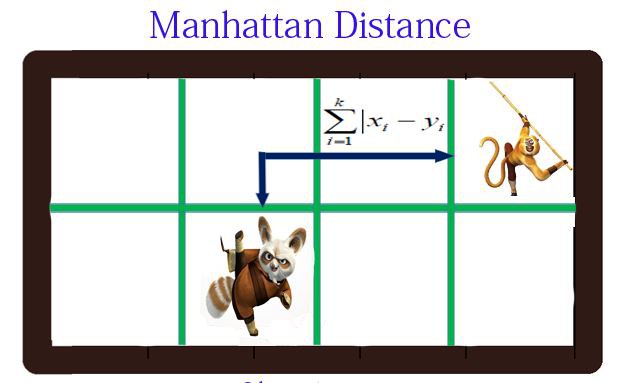
$$ Manhattan\_Distance = |x_1 - x_2| + |y_1 - y_2| $$

实现：

def manhattan_dist(x, y):
    return sum(abs(1-b) for a, b in zip(x, y))

3. 明科夫斯基距离(Minkowski Distance)

明氏距离是欧氏距离和曼哈顿的推广，是对多个距离度量公式的概括性表示，看看下图

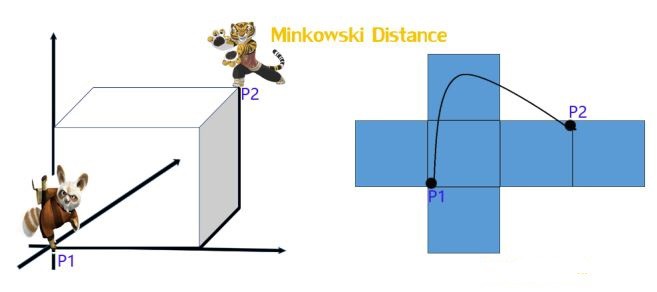
$$ Minkowski \_ Distance = (\sum_{i=1}^n |x_i - y_i|^p) ^{1/p} $$

• p=1 即为曼哈顿距离
• p=2 即为欧式距离
• p 为无穷大时即为比雪夫距离

实现：

def minikowski_dist(x, y, p):
    sumvalue = sum(pow(abs(a-b), p) for a,b in zip(x, y))
    mi = 1/float(p)
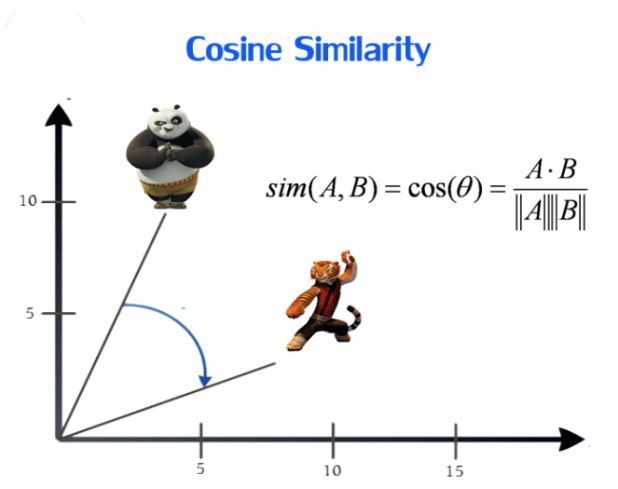
    return round(sumvalude ** mi, 4)

4. 余弦相似度(Cosine Similarity)

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小.

相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上.

实现：

import numpy as np

def cos_dist(x, y):
    num = sum(map(float, x*y))
    denom = np.linalg.norm(x) * np.linalg.norm(y)
    return round(num/float(denom), 4)

5. 雅可比相似性(Jaccard Similarity)

Jaccard 系数主要用于计算符号度量或布尔值度量的个体间的相似度，因为个体的特征属性都是由符号度量或者布尔值标识，因此无法衡量差异具 体值的大小，只能获得“是否相同”这个结果，所以Jaccard 系数只关心个体间共同具有的特征是否一致这个问题.

对于上面两个对象A和B, 我们用Jaccard计算它的相似性，公式如下

$$ Jaccard(X, Y) = \frac{X \cap Y}{X \cup Y} $$

首先计算出A和B的交集，以及A和B的并集：

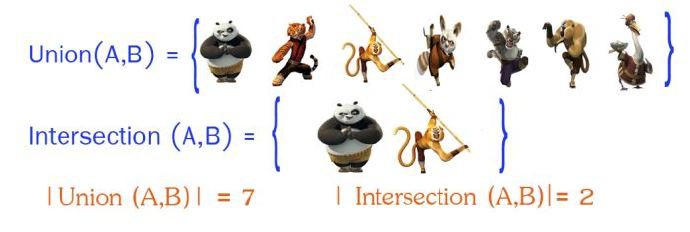
然后利用公式进行计算:

实现：

def jaccard_similarity(x, y):
    intersection_cardinality = len(set.intersection(*[set(x), set(y)]))
    union_cardinality = len(set.union(*[set(x), set(y)]))
    return intesection_cardinality/float(union_cardinality)

6. 实现汇总

similaritymeasures.py

#!/usr/bin/env python

from math import*
from decimal import Decimal

class Similarity():
    """ 
    Five similarity measures function 
    """
    def euclidean_distance(self,x,y):
        """ 
        return euclidean distance between two lists 
        """
        return sqrt(sum(pow(a-b,2) for a, b in zip(x, y)))

    def manhattan_distance(self,x,y):
        """ 
        return manhattan distance between two lists 
        """
        return sum(abs(a-b) for a,b in zip(x,y))

    def minkowski_distance(self,x,y,p_value):
        """ 
        return minkowski distance between two lists 
        """
        return self.nth_root(sum(pow(abs(a-b),p_value) for a,b in zip(x, y)),p_value)

    def nth_root(self,value, n_root):
        """ 
        returns the n_root of an value 
        """
        root_value  = 1/float(n_root)
        return round (Decimal(value) ** Decimal(root_value),3)

    def cosine_similarity(self,x,y):
        """ 
        return cosine similarity between two lists 
        """
        numerator = sum(a*b for a,b in zip(x,y))
        denominator = self.square_rooted(x)*self.square_rooted(y)
        return round(numerator/float(denominator),3)

    def square_rooted(self,x):
        """ 
        return 3 rounded square rooted value 
        """
        return round(sqrt(sum([a*a for a in x])),3)

    def jaccard_similarity(self,x,y):
        """ 
        returns the jaccard similarity between two lists 
        """
        intersection_cardinality = len(set.intersection(*[set(x), set(y)]))
        union_cardinality = len(set.union(*[set(x), set(y)]))
        return intersection_cardinality/float(union_cardinality)
    
def main():
    """ 
    main function to create Similarity class instance and get use of it 
    """
    measures = Similarity()
    print measures.euclidean_distance([0,3,4,5],[7,6,3,-1])
    print measures.jaccard_similarity([0,1,2,5,6],[0,2,3,5,7,9])

if __name__ == "__main__":
    main()

similarity_measures.py

#!/usr/bin/env python

from math import*
from decimal import Decimal

def euclidean_distance(x,y):
    return sqrt(sum(pow(a-b,2) for a, b in zip(x, y)))

def manhattan_distance(x,y):
    return sum(abs(a-b) for a,b in zip(x,y))

def minkowski_distance(x,y,p_value):
    return nth_root(sum(pow(abs(a-b),p_value) for a,b in zip(x, y)),p_value)

def nth_root(value, n_root):
    root_value  = 1/float(n_root)
    return round (Decimal(value) ** Decimal(root_value),3)

def cosine_similarity(x,y):
    numerator = sum(a*b for a,b in zip(x,y))
    denominator = square_rooted(x)*square_rooted(y)
    return round(numerator/float(denominator),3)

def square_rooted(x):
    return round(sqrt(sum([a*a for a in x])),3)

def jaccard_similarity(x,y):
    intersection_cardinality = len(set.intersection(*[set(x), set(y)]))
    union_cardinality = len(set.union(*[set(x), set(y)]))
    return intersection_cardinality/float(union_cardinality)

#print cosine_similarity([3, 45, 7, 2], [2, 54, 13, 15])
print euclidean_distance([0,3,4,5],[7,6,3,-1])
#print manhattan_distance([10,20,10],[10,20,20])
#print minkowski_distance([0,3,4,5],[7,6,3,-1],3)
#print jaccard_similarity([0,1,2,5,6],[0,2,3,5,7,9])