Caffe - Solver
Solver 通过协调网络的前向推断(forward inference) 和后向梯度(backward gradients) 进行参数更新,以进行模型优化.

网络学习可以分为:Solver 监督优化及参数更新和 Net 计算 loss 及梯度.
Caffe 提供的 Solvers 有:
- Stochastic Gradient Descent (
type: "SGD"), - AdaDelta (
type: "AdaDelta"), - Adaptive Gradient (
type: "AdaGrad"), - Adam (
type: "Adam"), - Nesterov’s Accelerated Gradient (
type: "Nesterov") and - RMSprop (
type: "RMSProp")
Solver 的主要作用:
- [1] - 支持优化记录(bookkeeping),并创建训练网络(learning)和测试网络(evaluation).
- [2] - 通过调用 forward/backward 进行迭代优化,并更新参数.
- [3] - 周期地评估(evaluation)测试网络.
- [4] - 保存优化过程中模型和优化器状态的快照.
其中,对于每一次迭代,
- [1] - 调用 forward 计算网络的输出和 loss.
- [2] - 调用 backward 计算梯度.
- [3] - 根据优化算法,进行梯度计算,更新参数.
- [4] - 根据学习率,历史记录和优化方法更新优化器状态.
Caffe Solvers 可以以 CPU 和 GPU 两种模式运行.
Forward 计算:
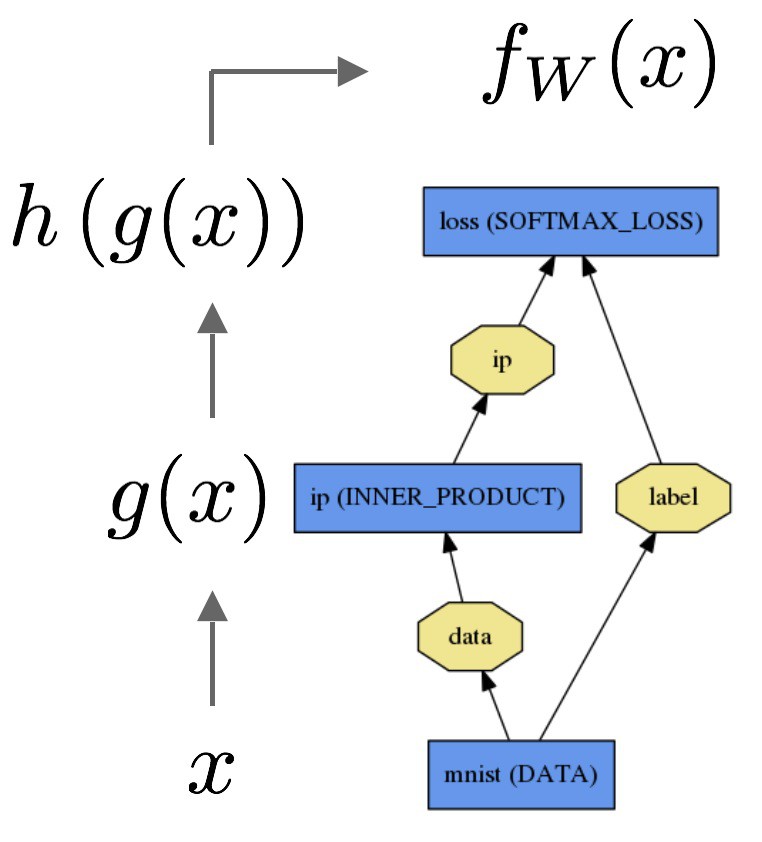
Backward 计算:
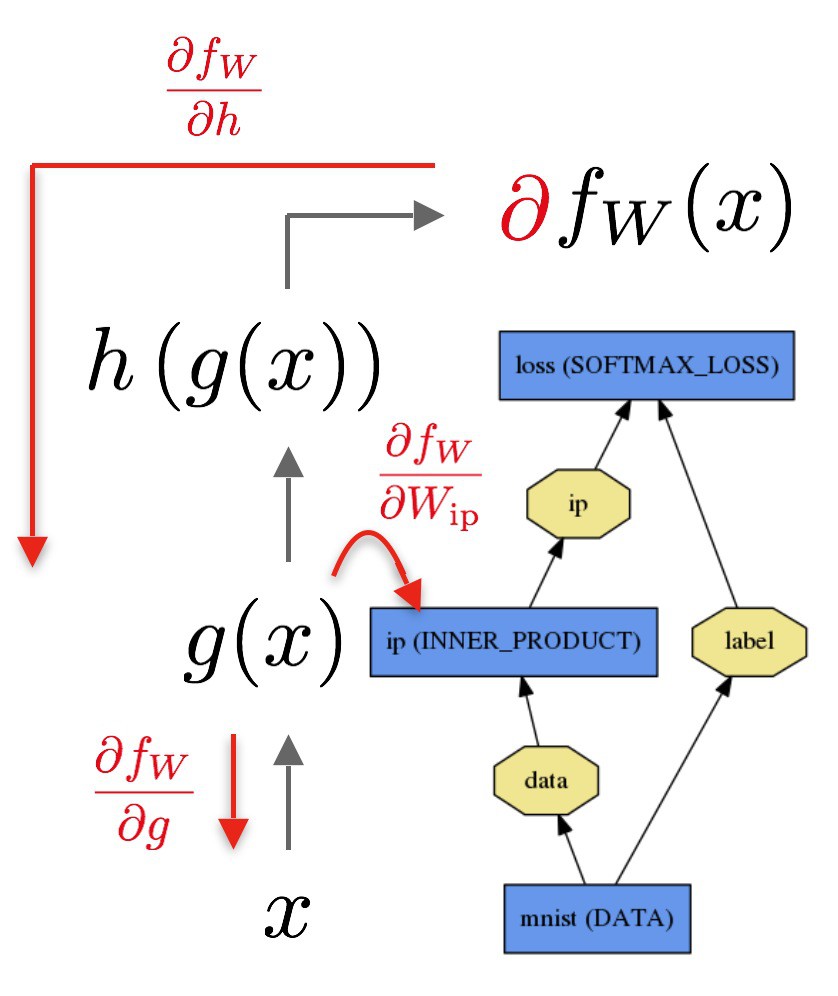
1. 优化方法
深度学习优化方法解决的问题是,最小化损失的一般问题.
对于数据集 $D$,优化的目标是,对整个数据集 $|D|$ 求平均损失:
$$ L(W) = \frac{1}{|D|} \sum _{i}^{|D|} f_W(X^{(i)}) + \lambda r(W) $$
其中,
$f_W(X^{(i)})$ 是对于数据样本 $X^{(i)}$ 的 损失值;
$r(W)$ 是正则项,$\lambda$ 为其权重.
在实际场景中,数据集样本总数 $|D | $ 会非常大,因此,在每次求解迭代中,一般采用小批量(mini-batch)数据 随机逼近目标 的方式,其中 $N << |D|$:
$$ L(W) \approx \frac{1}{N} \sum _{i}^{N} f_W (X^{(i)}) + \lambda r(W) $$
网络模型在 forward pass 中计算 $f_W$,在 backward pass 计算梯度 $\nabla f_W$.
网络的参数更新 $\Delta W$ 是由求解器(solver) 根据误差梯度(error gradient) $\nabla f_W$,正则梯度 $\nabla r(W)$ 以及其它参数进行迭代更新.
1.1 SGD
SGD, Stochastic Gradient Descent,随机梯度下降法.
SGD 是根据负梯度(negative gradient) $\nabla L(W)$和上次迭代的权重更新 $V_t$ 的线性组合来更新权重 $W$.
学习率(learning rate) $\alpha$ 是负梯度 $\nabla L(W)$ 的权重;
动量(momentum) $\mu$ 是上次权重更新 $V_t$ 的权重;
记,计算的更新值为 $V_{t+1}$,在 $t + 1$ 次迭代的更新的权重为 $W_{t+1}$,在给定上次迭代的更新的权重为 $V_t$ 和当前权重 $W_t$ 时,其迭代公式为:
$$ V_{t+1} = \mu V_t - \alpha \nabla L(W_t) $$
$$ W_{t+1} = W_t + V_{t+1} $$
学习率和动量设置的经验规则:
深度学习中,推荐的 SGD 的参数设置是,初始化学习率为 $\alpha \approx 0.01 = 10 ^{-2}$,当损失函数减少逐渐变缓时,以一个常数因子(如,10)衰减,重复几次该过程.
通常设置动量 $\mu = 0.9$ 等相似值. 通过在训练迭代时,平滑权重更新,动量能够使得 SGD 更平稳和快速.
在 solver.prototxt 中的定义:
base_lr: 0.01 # 学习率初始化值
lr_policy: "step" # 学习率策略,"steps"
# 在每 stepsize 次迭代时,
# 学习率以 gamma 因子衰减.
gamma: 0.1 # 以 10 的因子衰减学习率,
# 即,学习率乘以 gamma=0.1
stepsize:100000 # 每 100K 次迭代衰减学习率
max_iter:350000 # 总训练迭代次数
momentum: 0.9注:
在训练多次后,动量 $\mu $ 以 $\frac{1}{1-\mu}$ 的因子乘以更新的大小.
因此,增加 $\mu$ 是学习率 $\alpha$ 衰减的不错的策略. 反之,减少 $\mu$ 也可对应的提高学习率 $\alpha$.
例如,动量 $\mu = 0.9$,则有效的更新因子为 $\frac{1}{1 - 0.9} = 10$. 如果增加动量 $\mu = 0.99$,则更新因子增加为 $\frac{1}{1 - 0.99} = 100$,则将学习率 $\alpha$ 衰减了 10 (x0.1).
base_lr: 0.05
lr_policy: "multistep"
stepvalue: 150000
stepvalue: 300000
gamma: 0.1
momentum: 0.9
weight_decay: 0.0001
display: 10
max_iter: 6000001.2 AdaDelta
AdaDelta 是鲁棒的学习率调整方法,其是基于梯度的优化方法,参数更新公式为:
$$ (v_t)_i = \frac{RMS((v_{t-1})_i)}{RMS(\nabla L(W_t))_i} (\nabla L(W_{t^{'}}))_i $$
$$ (W_{t+1})_i = (W_t)_i - \alpha (v_t)_i $$
其中,
$$ RMS(\nabla L(W_t))_i = \sqrt {E[g^2] + \epsilon} $$
$$ E[g^2]_t = \delta E[g^2]_{t-1} + (1 - \delta)g_t^2 $$
# mnist_autoencoder_solver_adadelta.prototxt
base_lr: 1.0
lr_policy: "fixed"
momentum: 0.95
delta: 1e-8
weight_decay: 0.0005
type: "AdaDelta"
display: 100
max_iter: 650001.3 AdaGrad
AdaGrad, 即 adaptive gradient,自适应梯度法.
AdaGrad 也是基于梯度的优化方法,AdaGrad attempts to find needles in haystacks in the form of very predictive but rarely seen features.
给定所有先前迭代的更新信息 $(\nabla L(W))_{t^{'}}$, 其中,$t^{'} \in \lbrace 1, 2, ..., t \rbrace$,权重更新公式为:
对于权重 $W$ 的每个一个元素,
$$ (W_{t+1})_i = (W_t)_i - \alpha \frac{(\nabla L(W_t))_i}{\sqrt{\sum _{t^{'}=1}^t} (\nabla (W_{t^{'}}))_i^2} $$
实际应用场景中,对于权重 $W \in \mathcal{R} ^d$,AdaGrad 仅采用 $\mathcal{O}(d)$ 的历史梯度信息.
# mnist_autoencoder_solver_adagrad.prototxt
base_lr: 0.01
lr_policy: "fixed"
weight_decay: 0.0005
solver_mode: GPU
type: "AdaGrad"
display: 100
max_iter: 650001.4 Adam
Adam 也是基于梯度的优化方法.
Adam 包括自适应矩估计(adaptive moment estimation) $(m_t, v_t)$ .
Adam 可以看作 AdaGrad 的一种泛化.
Adam 更新公式为:
$$ (m_t)_i = \beta_1(m_{t-1})_i + (1 - \beta_1)(\nabla L(W_t))_i $$
$$ (v_t)_i = \beta_2(v_{t-1})_i + (1 - \beta_2)(\nabla L(W_t))_i $$
$$ (W_{t+1})_i = (W_t)_i - \alpha \frac{\sqrt{1 - (\beta_2)_i^t}}{1 - (\beta)_i^t} \frac{(m_t)_i}{\sqrt{(v_t)_i} + \epsilon} $$
Adam: A Method for Stochastic Optimization 中的默认值为 $\beta_1 = 0.9, \beta _2 = 0.999, \epsilon=10^{-8}$.
Caffe 中 $momentum = \beta _1, momentum2 = \beta _2, delta = \epsilon$.
# lenet_solver_adam.prototxt
base_lr: 0.001
momentum: 0.9
momentum2: 0.999
# since Adam dynamically changes the learning rate,
# here, set the base learning rate to a fixed value.
lr_policy: "fixed"
type: "Adam"
display: 100
max_iter: 100001.5 Nesterov
Nesterov, Nesterov’s accelerated gradient.
更新公式类似于 SGD:
$$ V_{t+1} = \mu V_t - \alpha \nabla L(W_t + \mu V_t) $$
$$ W_{t+1} = W_t + V_{t+1} $$
# mnist_autoencoder_solver_nesterov.prototxt
base_lr: 0.01
lr_policy: "step"
gamma: 0.1
stepsize: 10000
weight_decay: 0.0005
momentum: 0.95
type: "Nesterov"
display: 100
max_iter: 650001.6 RMSprop
RMSprop 也是一种基于梯度的优化方法,类似于 SGD. 其更新公式为:
$$ MS((W_t)_i) = \delta MS((W_{t-1})_i) + (1 - \delta)(\nabla L(W_t))_i^2 $$
$$ (W_{t+1})_i = (W_t)_i - \alpha \frac{(\nabla L(W_t))_i}{\sqrt{MS((W_t)_i)}} $$
其中,$\delta$ (rms_decay) 的默认值为:$\delta=0.99$.
# lenet_solver_rmsprop.prototxt
base_lr: 0.01
momentum: 0.0
weight_decay: 0.0005
lr_policy: "inv"
gamma: 0.0001
power: 0.75
type: "RMSProp"
rms_decay: 0.98
display: 100
max_iter: 10000