很多三维建模相关专业的学生在学习建模软件时常常会感到困惑,由于不了解三维建模中各种隐含的规定,缺乏三维建模的相关知识,常常误以为是软件的bug,最后往往变成了“国家一流软件安装与卸载师”,三维建模的学习过程也逐渐变成了“从入门到放弃”的过程. 那么我们应该如何去学习三维建模呢?
我们可以先从计算机中常见的几何表示方法开始,本节将讨论了计算机中不同的三维几何表示方法,了解这些方法可以对当前计算机建模软件的建模方式有一个宏观的认识,这有助于在完成设计或计算任务前选择恰当合适的软件进行使用和学习. 当然,对于有些方法可能过于抽象,读者不需要完全理解,有一个大体的认识即可.
参数表达与隐式表达
曲面通常有两种表示方法:参数表达 (Parametric representations) 和 隐式表达 (Implicit representations).
根据《Polygon Mesh Processing》中的解释,参数曲面是由向量值的参数化函数 $f: \Omega \rightarrow S$ 来定义的,它将二维参数域 $\Omega \rightarrow R^2$ 映射到了曲面 $S = f(\Omega) \subset R^3$ 上.
而隐式曲面是由一个方程来定义的,方程左侧为表示曲面上点的坐标的三维参数的标量表达式,等式右边为 0. 为方便理解,我们以一个平面上的单位圆为例, 它的参数表达为
$$ f: [0, 2|\pi] \rightarrow R^2, t \rightarrow (cost, sint) $$
隐式表达为:
$$ F: R^2 \rightarrow R, (x,y) \rightarrow \sqrt{(x^2 + y^2)} -1 $$
通俗的理解是,参数表达在曲面上的点都可以找到明确的坐标定义,而隐式表达不会显式地表达明确的点的位置,而是去表达这些点的位置所满足的关系,它是通过点坐标不同分量之间的关系来定义的. 例如在单位圆示例中,参数表达直接表示了所有点的坐标,即 $(cost, sint)$;而隐式表达只表示出了两个分量所满足的关系,如果我们想要知道每个点的坐标,需要通过给定的关系来计算得到.
由于两种表达方式的定义方法不同,它们也有着不同的特性.
由于参数表达直接记录了点的坐标,因此是一种很直观的表示方法,计算机可以直接读取坐标来显示出几何. 此外,由于它是通过参数方程来表示曲面的,所以很多在曲面上的三维问题可以被转化成二维参数域上的问题. 但是判断位置关系等问题对它来说十分棘手,需要通过一些算法来解决,计算成本较高. 例如要想判断一个点是否在物体内部,对于参数表达的曲面来说是一件成本较高的事. 然而这对于隐式表达就会十分容易,因为它可以直接将点的坐标代入到方程中,通过计算即可知道该点与物体之间的位置关系,当然,隐式表达的缺点就是表达不直观,仅根据表达式很难知道它所表示的物体,尤其是对于复杂几何,其显式地表现出几何的成本过高. 因此两种表示方法各有优劣,需要根据实际需求和两种表示方法的特点来选取成本较低的表示方法. 下面我们来逐一介绍常用的几何表示方法.
| 参数表达 | 隐式表达 | |
|---|---|---|
| 定义 | 由参数方程定义,明确地表达了点的位置 | 由隐式方程定义,定义了点坐标中不同的分量所满足的关系 |
| 优点 | 1. 表示直观;2. 方便将三维问题转化为二维参数域上的问题 | 求交等问题成本更低 |
| 缺点 | 在求交等问题上成本过高 | 表达不直观 |
参数表达方法
点云
从相对容易理解的参数表达开始入手,通常在描述一个三维模型时,最基本的描述方式是使用点去描述,但是要想表达出一个三维模型,需要大量且密集的点,这些点称之为点云 (Point Cloud) .
三维空间中一个点由三个方向的坐标构成,通常记作 (x,y,z),因此,点云可以被视作是一堆点的集合,存储时即可用一系列 (x,y,z) 坐标来表示.
注意:
[1] - 描述三维模型的点云数据是无序排布的,这意味着点云在三维空间中,仅表示一系列点,点与点之间没有任何联系.
[2] - 点云是表示三维几何模型中最简单的方法,它可以表示任意类型的几何物体,代价是必须拥有足够密集的点云信息才能避免物体失真.
[3] - 点云通常是由三维扫描得到的,三维扫描仪通过记录空间中被扫描物体的点云信息,再使用表面重建算法来得到一个完整的三维扫描模型的. 因此,点云通常会被转化成网格来做后续处理.

样条曲面
在当今的CAD软件中,样条曲面 (Spline Surfaces) 是最常用的表示方法之一,尤其是在机械、工业设计等领域,对曲面质量要求较高的行业中应用广泛.
样条曲面表达一般指非均匀有理B样条 (NURBS),它是由分段多项式或有理B样条基函数来描述的.
NURBS建模可以使用户设计出质量极高的曲面,但是对于一些较复杂的几何形体,它需要通过多张曲面拼接来实现,为了保证曲面质量,用户需要处理大量由拼接引起的曲面连续性问题,这带来了高昂的建模成本. 另一个缺点是,添加更多顶点操作需要通过分割参数域来实现,这使得曲面的局部修改与设计变得相对困难. 对于NURBS建模的更多细节,可以参阅[Farin 97,Piegl and Tiller 97,Prautzsch et al. 02].
多边形网格
在CAD软件中,除样条曲面表达外,另一种被广泛应用的三维模型表示方法就是多边形网格 (Polygon Mesh). 它通常是指由三角形或四边形拼接而成的几何模型,几乎任何几何形状都可以通过拆分成无数三角形或四边形面片来表达. 由于网格在图形学领域被广泛研究,各种处理算法层出不穷,因此它已经变成了当前图形学最普遍的图形表示方法. 无论是游戏场景建模、概念设计建模还是分析与模拟,都是通过编辑和处理网格单元来实现的.

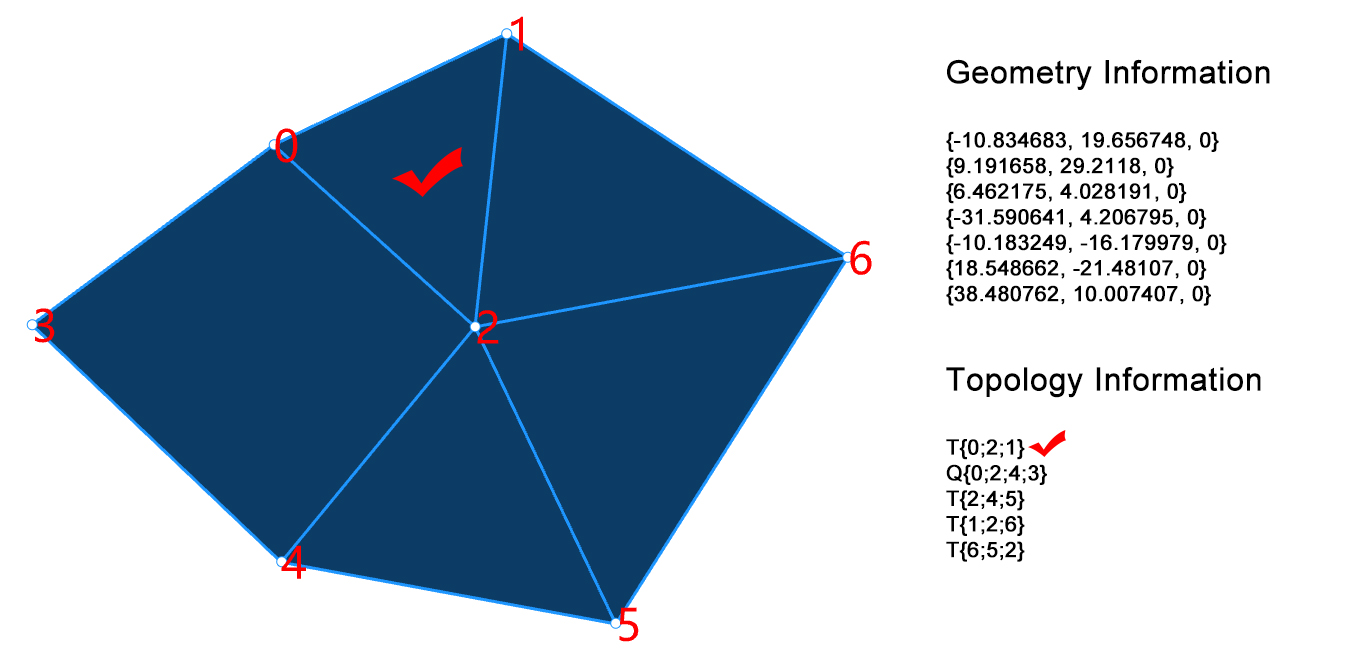
最基础的网格数据结构将网格所描述的信息分成了两个部分:几何信息 (Geometry Information) 和拓扑信息 (Topology Information) . 几何信息描述了网格上的顶点的坐标,拓扑信息描述了网格上的顶点的连接关系.
图2展示了一个网格模型的实例,左侧网格模型上的顶点按照顺序标记了它们的索引 (Index) . 右侧几何信息中,按顺序描述了每一个顶点的三维坐标,例如0号顶点的坐标为{-10.834683, 19.656748, 0},由于这是一个平面网格模型,因此Z坐标均为0. 拓扑信息描述了每一张网格面由哪些顶点构成,其中T表示三角形 (Triangles),Q表示四边形 (Quadrangle),例如T{0; 2; 1} 描述了第0张网格面片为三角形,它是由第0、2、1号点按顺序构成的三角形.
细分曲面
细分曲面是一种通过粗糙网格来控制的

References
[1] Botsch, M., Kobbelt, L., Pauly, M., Alliez, P. and Lévy, B., 2010. Polygon mesh processing. CRC press.
[2] Piegl, L. and Tiller, W., 2012. The NURBS book. Springer Science & Business Media.
[3] Farin, G., 2014. Curves and surfaces for computer-aided geometric design: a practical guide. Elsevier.
网格
网格通常指三角形、四面体及它们所构成的图形.
先来设想这样的问题,对于一个球体的表达,可以有两种认识:其一是将球认为是球的外壳,即将这个球看作一个闭合成球这个形状的曲面,生活中举例的话比如足球,只有外皮,里面是空的;另一种是将球认为是填实的实体,举个例子就比如雪球,里面都是雪,很厚实. 这两种表达方法各有优劣,
对于“球壳”来说,对它进行一些剪切、拼贴、变形等操作都相对较容易,在网格处理上大多都会选择这样的表达方法,如Rhinoceros、Maya;
对于实体球来说,一般用于结构工程的有限元分析,可以想象,结构分析当然要认定一个结构体是密闭填实的,只计算“外皮”和计算实体是完全不同的两个概念,因此在计算一些需要考虑到内部填充的操作时必须将物体考虑成密闭实体,这类软件的代表就如结构专业常用的有限元分析Abaqus.
前者的单纯形就是三角形,后者是四面体. 由于四面体填充的形式一般仅在结构分析中会涉及,非结构和计算机专业的人一般不会过多去关注这方面,这里是介绍二维单元作为网格基本单元的情况.
网格的基本单元除了三角形还有四边形(四边形不叫作单纯形了,但仍然是网格的基本单元). 为什么又多了一个四边形呢?这里又得提两个概念了,结构化网格和非结构化网格.
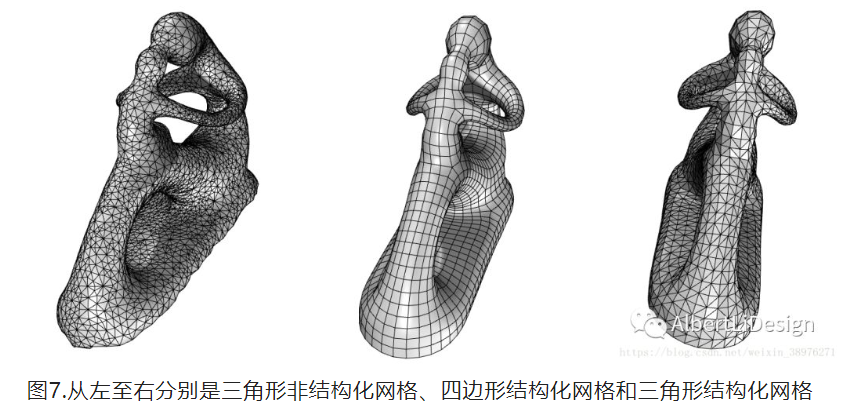
结构化网格是说,这个网格模型的大多数顶点所连接的网格面的数目(网格顶点的价)是相等的. 如果这句话现在理解不了也没关系,因为大多出情况都没有那么严格,比较直观的理解就是一张网格拟合的曲面,看上去结构线清晰分明就是结构化网格(如图5、6).
非结构化网格就是与结构化网格相对,看上去乱七八糟的单元排布就是非结构化网格. 通常我们得到的三维扫描模型都是非结构化网格,这样的网格如果每个网格面片的大小近似相等的话那还好说,但是如果大小变化剧烈,就很难继续编辑,网格质量糟糕,一般必须通过算法或人工重建才能继续使用.

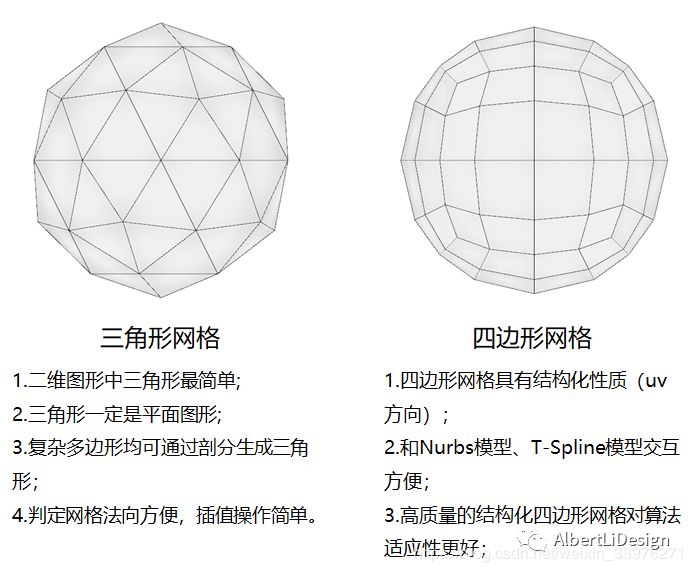
然而四边形,作为具有明显方向特征的基本单元,通常就被用作表达结构化网格了. 四边形网格和三角形网格的特性如图8所示
网格的数据结构
计算机并不认识图形,要想让计算机知道,这里有一个三角面,那就必须用逻辑关系来表达出来.
比如,三角面由三个顶点三条边和一张面构成(点线面全了),那么,顶点在空间中能表达出来,就是三个三维坐标;边可以看作是两个顶点放在一起,也就是一个有顺序的,从一个三维坐标到另一个三维坐标的关系;面则可认为是三条边有序排列在一起的关系. 再傻瓜一点说,就是空间三个顶点A、B、C,把顶点A和顶点B放在一起就能表示从A到B这条边,其他边的表示依次类推,面的表示就是把三个顶点按照某一顺序放在一起就是一张面.
也就是说,网格最最底层的构成就是顶点的坐标和它们相连的关系. 由此引出,网格的存储信息分为两部分,几何信息(顶点坐标)和拓扑信息(顶点连接关系).
网格模型的数据存储有很多种方式,当前数据结构有很多,比如两个最常用的,Faced-Based Data Structures和Half-Edge Data Structure.
Faced-Based Data Structures
Faced-Based是最简单直观的数据结构,只存储了顶点坐标和顶点拓扑关系两种数据的数据结构. 但看似简单的东西其实也还有玄机.
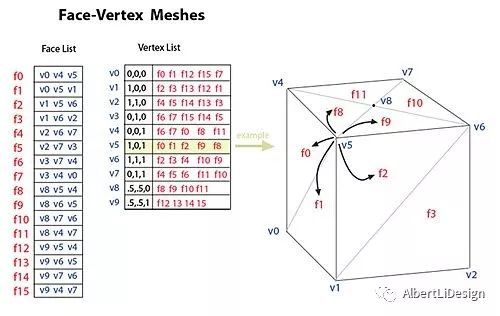
Half-Edge Data Structure
Half-Edge Data Structure 直译就是半边数据结构,半边是非常好用的网格数据结构,它在相邻元素查找的问题上十分方便. 这种数据结构是以网格边为主导的,是将每条边分成两条半边,这两条半边的长度与原网格边相同,但是方向相反. 可以理解为把一条边拆成了两个方向相反、长度相同的向量,向量都是有始有终的,因此可以很容易将一个网格的所有半边首尾相接连起来,这也正是这种数据结构的妙处所在.
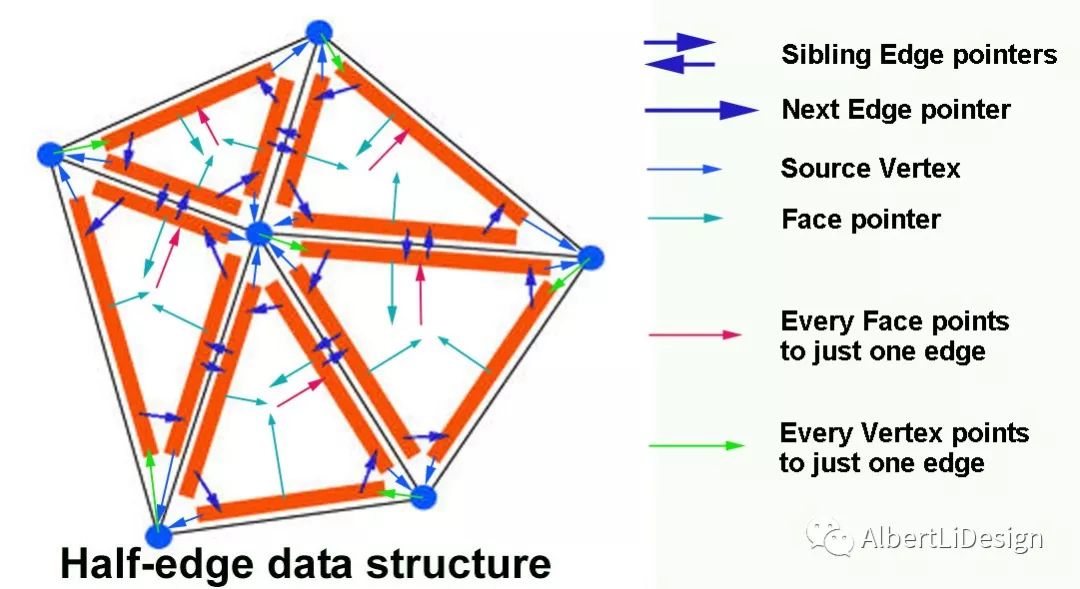
在解决不同的网格编辑问题时,数据结构的选择非常重要,在运行程序时,合适的数据结构能大大提高运行效率. 同样的算法,用不同的数据结构来实现,其运行效率会有很大的差别.
一般来说,判定一个网格的数据结构是否适合解决这个问题的依据有以下几点:
[1] - 构建数据结构的时间复杂度
[2] - 进行查询操作的时间复杂度
[3] - 网格编辑操作的时间复杂度
[4] - 空间复杂度
网格细分
网格数据大多数由三角形或四边形组成. 网格细分技术为分割曲面提供了解决方案. 这种技术的核心是关注如何通过细分算法(Subdivision)计算来用大量的较小的网格面来替代原来的曲面,从而细分并优化输入的基础网格面. 并且由此产生的精密网格还可以使用相同的算法来产生更精密的网格,如此可以反复迭代. 随着迭代步的增加,网格的数量也不断地翻倍,从而更加逼近于精确、光滑的初始曲面.
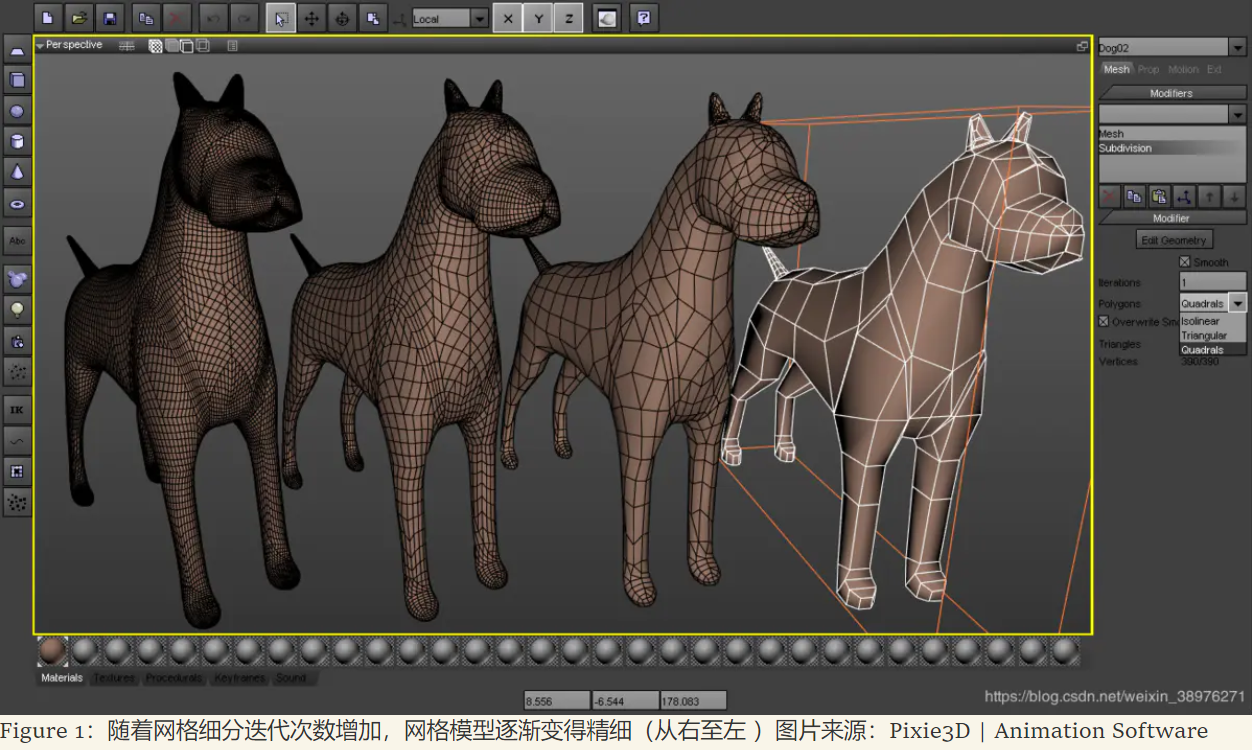
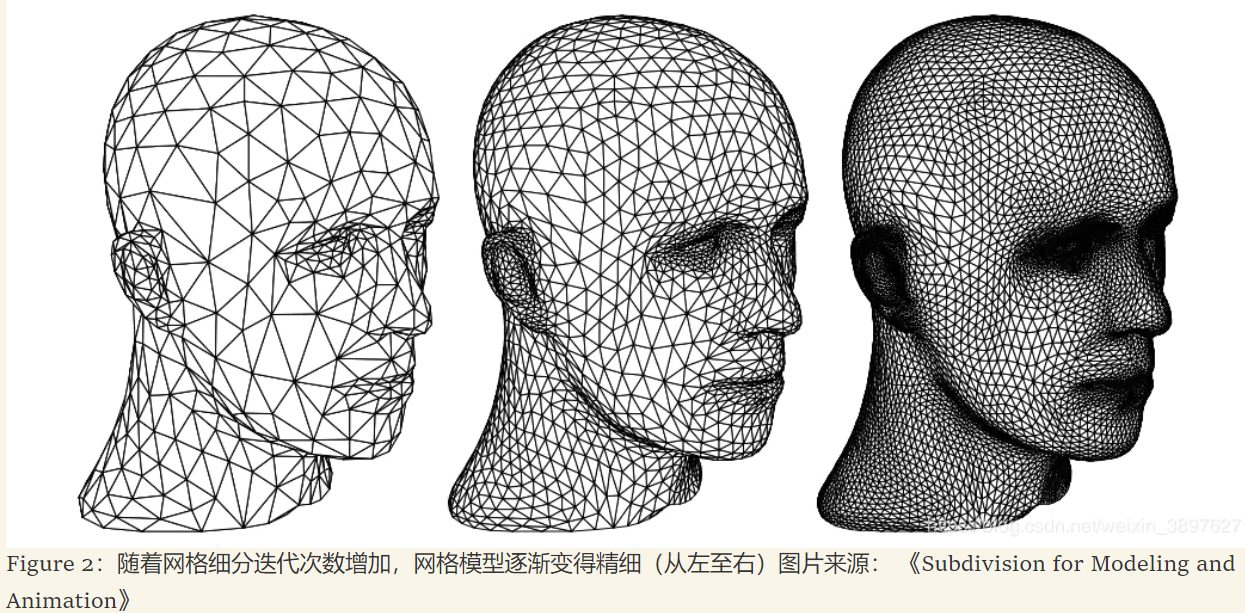


网格细分可以看作是一种圆滑的过程,细分得到的网格子顶点坐标是由周围相邻父顶点的平滑平均值产生. 用这种方式,网格的坐标被圆滑,形成更接近初始的近似曲面. 这一点已经被证明(Zorin et al.,2000),这种生成的近似曲面在非边界和非奇异顶点处都是C2连续的,这意味着形态表面(没有缝隙)、表面切线(没有折痕)以及切线的变化率(在视觉反射中没有变形)都没有突变(这三点分别是C0,C1和C2连续性的判断标准). 这也是细分网格看上去特别美观的原因.
圆滑过程的另一个优点是,细分不仅能可以圆滑顶点坐标,任何一组与顶点关联的数据都会被圆滑,如果一个初始的粗糙网格中每一个顶点附带着一个颜色的信息,所有连续细分的网格都能够自动匹配圆滑曲面上的颜色. 可以类似地应用于更多实际的参数,例如顶点携带的贴图信息、应力值、立面渗透率或透明度值,百叶窗角度或者覆层的偏移距离. 在基础网格上,这些数据可以被定义在所需要的顶点上,细分网格后,这些信息将完全以与顶点位置相同的C2连续的方式均匀地分布在整个曲面上.
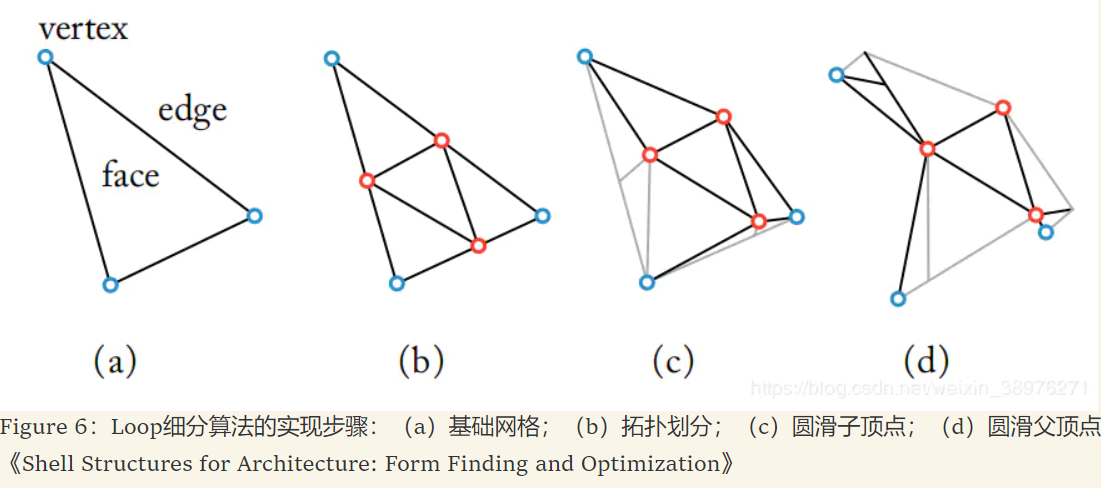
Loop细分算法原理
Loop细分算法(Loop,1992)是一种应用在三角形网格的算法,如图6所示,这是从一个球形网格中提取的一张网格面,蓝色顶点为父顶点,即网格面原有的顶点,红色顶点为新创建的子顶点,每个三角形上的每条边都被新引入的子顶点分割成了两段,然后每一个三角形都被四个新的小三角形代替.