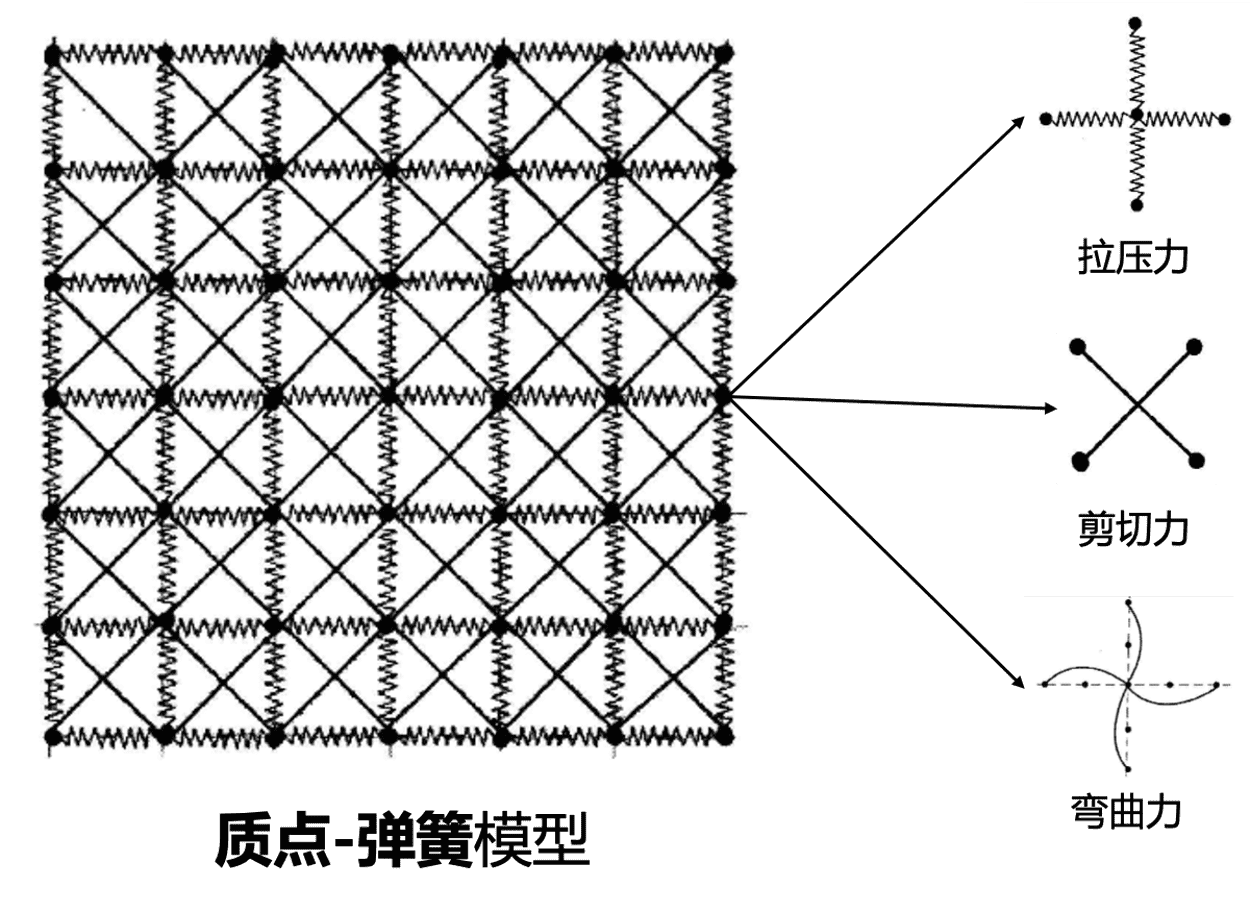
质点-弹簧模型是将布料看作离散的指点,质点之间用弹簧相连,将织物的运动划分为拉伸压缩变形、相邻弹簧的剪切变形和弯曲变形,用不同类型的弹簧去约束质点各个方向的受力状态。
质点-弹簧模型动态仿真的过程简单来说就是:初始时刻在屏幕上画出所有质点和弹簧的位置状态,下一个时刻再计算所有质点和弹簧位置状态,以此类推逐时刻计算,连续起来实现动态效果。其中获得每个点的位置状态,是通过对受力、速度、加速度分析,构建对应微分方程组,再通过欧拉法等方式求解微分方程得到的。

[服饰3D柔性渲染调研及实践[转]](https://aiuai.cn/aifarm1890.html)
网格质点弹簧模型
From: GPU布料物理模拟入门 - 知乎
1. 弹性力
这是目前用的比较多的一种布料物理建模。思路是将一块布料视作由一个个质点构成的网格,网格之间由弹簧相连接。如下图:

质点之前的连接分为三类,分别用以模拟材料中的三种力:
- 上下左右相邻质点连接,模拟结构力(Structural),如拉伸和收缩。
- 对角线连接,模拟剪力(Shear)。
- 上下左右跨一个质点连接,用以模拟材料弯曲的力(Flexion)。
弹簧的力学模型满足胡克定律:
即,
$$ F = -K_s \Delta x $$
其中,$\Delta x$ 表示弹簧的伸缩量.
把结构力、剪力、弯力加起来称为布料的内部受力,记为 $F_i$.
2. 阻尼力
质点在运动的时候,通常是有能量耗散的。弹簧振子如果没有耗散就会永远的震动下去。这不符合现实。因此需要加入阻尼力来模拟这种耗散。公式为:
$$ F_d = - C_d v $$
其中,$C_d$ 为阻尼系数,$v$ 为运动方向.
3. 重力
布料通常还会受重力,记为 $F_g$
$$ F_g = mg $$
其中,$g = 9.8$ 为重力加速度,垂直向下.
4. 外力
布料还会受一些外力,例如风力等等。记录为 $F_e$.
5. 运动方程
综合以上几种受力,这样就得到了质点的受力计算方式:
$$ F = F_i + F_d + F_g + F_e $$
根据牛顿第二定律,可以计算出质点的重力加速度:
$$ a = \frac{F}{m} $$
有了加速度,可以计算质点的速度:
$$ v = v + a \Delta t $$
然后计算质点的位移:
$$ x = x + v \Delta t $$
重复迭代以上步骤,即可以模拟布料运动。是最简单的一种模拟方式.
PBD算法
PBD算法的全称是Position-Base-Dynamic,顾名思义,它是一种计算机视觉方面的动态模拟算法,主要用于各种需要实时模拟的场景。
相比起过去的基于真实物理规则的模拟来说,PBD算法具有这样的特征:
- [1] - 直接基于位置而非受力情况来计算位置。计算的结果虽然并不是完全真实的物理模拟,但是可信度很高。
- [2] - 性能更好,而且性能消耗的力度可控,可以根据实际应用中对真实性的需求强度来决定计算量。
- [3] - 实时计算,动态模拟。
从这两个特征看出,PBD算法最适合的就是游戏、电影、VR之类的场景,不需要百分之百的完全真实,而是“看起来像”就可以了。
由于PBD算法是一种实时模拟,尤其受到游戏行业的青睐。事实上,目前PBD算法在游戏领域也已经得到了广泛的应用,NVIDIA的Flex引擎包、网易的一些游戏都已经在使用该算法。
算法流程

图中 x 为当前质点位置, p为预测质点位置。可以看到:
- 算法在每一帧开始时,会根据外力和阻尼先于计算一个位置(p)
- 根据当前位置(x)和预测位置(p),去进行碰撞检测,如果发现有碰撞,就生成一个碰撞约束
- 迭代求解所有约束,最终会得到新预测位置p
- 利用p - x 来计算速度v,并将p赋值给x
- 最后再计算一遍速度(处理碰撞反弹之类速度变换)
关于外部力的定义:
像重力、风、可以视为外部力,但是像质点之间的相互作用,通常视为内部约束,而非力。同样外部物体对质点的碰撞,也视为碰撞约束而不是外部力。
具体的,
1-3行,把想要模拟的复杂系统,例如流体、布料、头发等,拆解成一个个质点,质点拆解得越多,消耗的性能就越多,效果也就越逼真,可以根据自身的实际需求来进行拆解。x 指的是质点 i 的位置,v 指的是质点的初速度,m 是质点的质量(并不一定是真实质量,而是在整个系统中的相对值),w是 m 的倒数。(为啥要弄个倒数出来呢,主要是方便计算,把除法变成乘法,而且还可以把一些静止质点视为质量无限大,直接把w设成0即可。)
4-17行,是一个大循环,不断更新每个质点的位置。
5 行,根据系统的受力情况来更新每个质点的速度v,比如说,当系统仅受到重力的时候,这个复杂的式子就变成了 vi=vi+∆t*G,G是重力(在unity中就是一个Vector3(0, -9.8, 0))。∆t 指的是时间的变化量,比如说一秒60帧,每帧迭代3次的话,∆t就是1/60/3秒。
6行,对速度施加系统阻尼。
7行,p 是一个预测位置,是每个质点在整个算法完成后的新位置。该位置的初始值就是质点的初始位置x,这一行的作用是将物体当前的位置加上 速度*时间 之后得到一个新位置。
8-11行,是算法的重点。这几行的作用是,对质点的新位置 p 加上碰撞和约束的修正。举例来说,上一步算出来下一行某个质点的位置是(0,-1,0),但是实际上在 y=0 处有一个平面,这个位置穿墙了,这时候我们就要基于墙面的碰撞来对p做一个修正。(在进行约束修正的时候,这里有一个循环,迭代了一定的次数。为什么要迭代呢?最重要的原因之一就是计算机在对所有质点进行计算的时候,是按照循环的顺序从1到n依序计算的,但是在真实环境下这些质点应该是同时进行的,这就导致在计算后面的约束时可能会把之前的计算结果污染掉,因此这里需要反复计算几次来更加接近真实情况。)
“约束”是一个什么概念呢?顾名思义,约束就是对质点运动的一些限制条件,让质点不能随心所欲乱动。举个例子来说,最简单的约束就是刚体约束,可以想象一下两个质点中间有一个小棍连接,不管两个小球怎么翻滚怎么运动,这个小棍不能断,这两个质点之间的相对距离都是不变的。
假设小球就是一个个质点,那么这些质点之间的约束就是典型的刚体约束,整个系统可以旋转可以运动,但是小球和小球之间的相对位置不变。
除了刚体约束之外,很常见的约束还有弹性约束、密度约束等。在根据速度得到新的位置之后,对新的位置进行碰撞和约束的修正,得到修正后的位置。
12-16行,本轮计算完毕,根据新位置和旧位置得出新的速度,然后把旧的位置更新,得出结果。