神经网络是由一系列线性和非线性模块的组合. 通过巧妙的网络设计,可以实现对任何数学函数的逼近,如,基于非线性决策边界的分类(separates classes with a non-linear decision boundary).
虽然神经网络具有直观和模块化的特点,但是一个往往并未深入解释的问题是,网络更新可训练参数的反向传播技术(backpropagation technique for updating trainable parameters).
因此,本文主要介绍的是,从零开始构建一个神经网络,并通过模块化的图片例示,深入理解神经网络的内部实现.
机器学习模型的调试是一个复杂的任务. 经验上来说,数学模型在开始尝试的时候可能不会是期望的情况,比如,可能对于新数据的精度较低,花费较长的训练时间或者金钱,返回大量的假阴性(false negatives)结果或者大量的 NaN 预测结果等. 对此,有一些经验:
[1] - 如果训练时间过长,一种可能的做法是,增大 minibatch 的大小,以减少训练样本的方差(variance),有助于算法收敛.
[2] - 如果得到 NaN 预测结果,可能是算法接收到较大的梯度值,导致内存溢出(memory overflow). 可以将其视为多次迭代后的连续矩阵乘法. 减小学习率,可能会有主于减少这些值的大小. 减少网络层数,可以减少矩阵乘法的数量. 梯度裁剪(clipping gradients) 可以显式的解决该问题.
1. 神经网络
如图,给出了神经网络训练时所涉及的部分数学公式:

[1] - 输入Input X
X 为送入神经网络的原始数据,数据格式为矩阵形式,其中,矩阵的行表示一个数据样本,矩阵的列表示维度.
[2] - 权重Weights W1
W1 对输入 X 进行映射到第一个隐藏层 h1. 权重 W1 作为线性核.
[3] - Sigmoid 激活函数
Sigmoid 激活函数用于防止隐藏层 h1 的输出超出范围,并归一化到 [0, 1] 区间. 其输出是一个激活值数组:h1 = Sigmoid(WX).
以上这些操作只是一种线性系统的计算,其并不能对非线性进行建模. 不过,如果再新增加一个或多个网络层,加深模块化网络的深度,则会发生一些变化. 神经网络越深,越可以学习到更加细致的非线性,也可以解决更复杂的问题.
2. XOR 非线性函数实例
这里以 XOR 函数为例,从零开始构建一个神经网络. XOR 非线性函数仅是随机选择,非特意指定. 如果没有 BP 计算,XOR 函数很难学习采用一条直线进行分类(separate classes with a straight line).
如图: XOR 函数的输出,一条直线很难区分 0s 和 1s.

网络的拓扑结构比较简单:
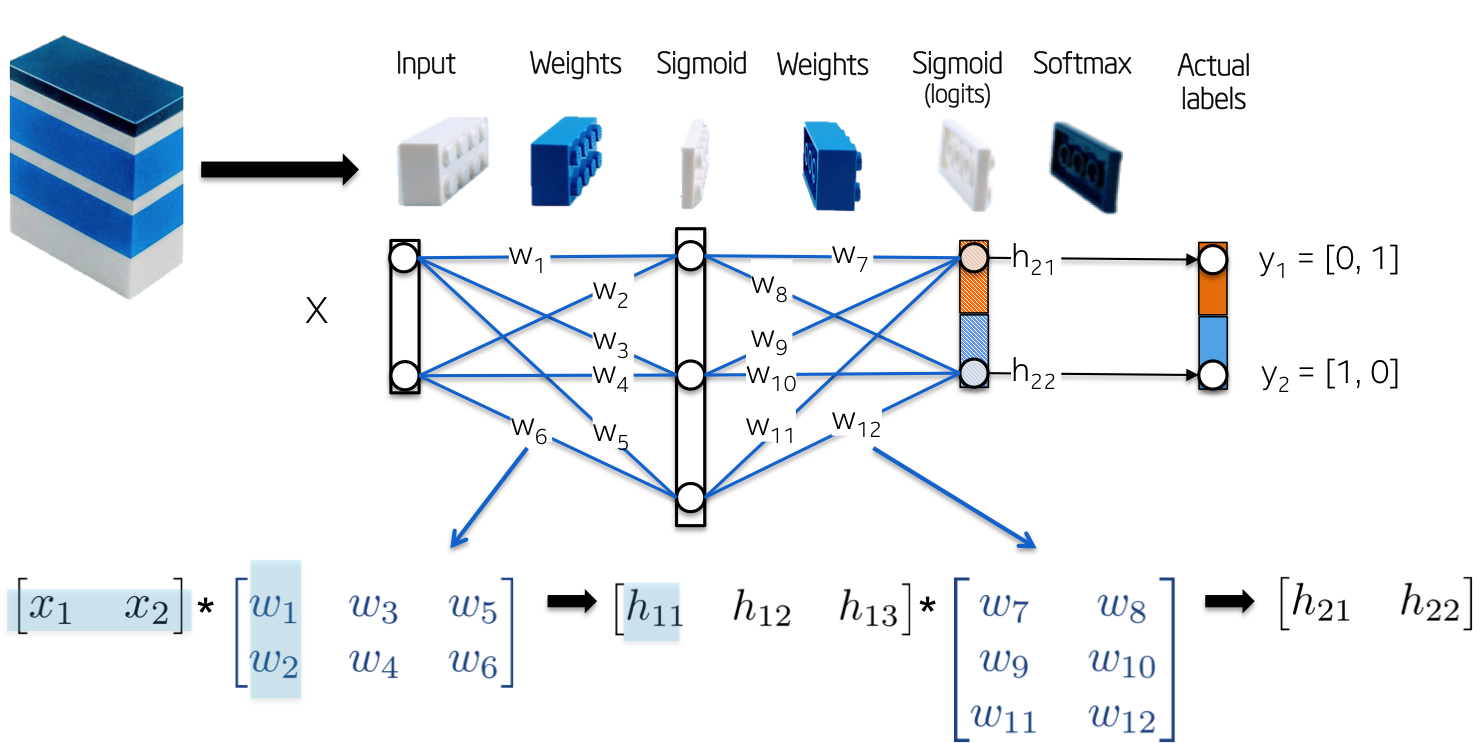
[1] - 输入Input X,二维向量;
[2] - 权重Weights W1,2x3 的矩阵,随机初始化矩阵的元素值.
[3] - 隐藏层Hidden layer h1,包括三个神经元. 每个神经元的输入是观察值的加权和,如下图的 green 高亮的内积部分:z1=[x1, x2][w1, w2].
[4] - 权重Weight W2,3x2 的矩阵,随机初始化矩阵的元素值.
[5] - 输出层Output layer h2,包含两个神经元,因为 XOR 函数返回的值是 0(y1=[0, 1]) 或 1(y2=[1, 0]).
如图:
接着,进行模型训练. XOR 函数的示例里,可训练参数只有权重参数. 不过,最新的网络结构研究中,探索了更多类型的参数,如网络层之间的短连接(shortcuts)、正则化分布、拓扑、残差、学习率等.
BP(Backpropagation) 是用于朝某个方向(gradient)更新权重的方法,其主要通过对批量的标注数据的,计算最小化预定义的误差度量,即损失函数. BP 算法已经被多次重复研究,在反向累计模式中,作为更通用的自动微分(automatic differentiation) 的一种特例.
2.1. 网络初始化
采用随机值初始化网络权重.
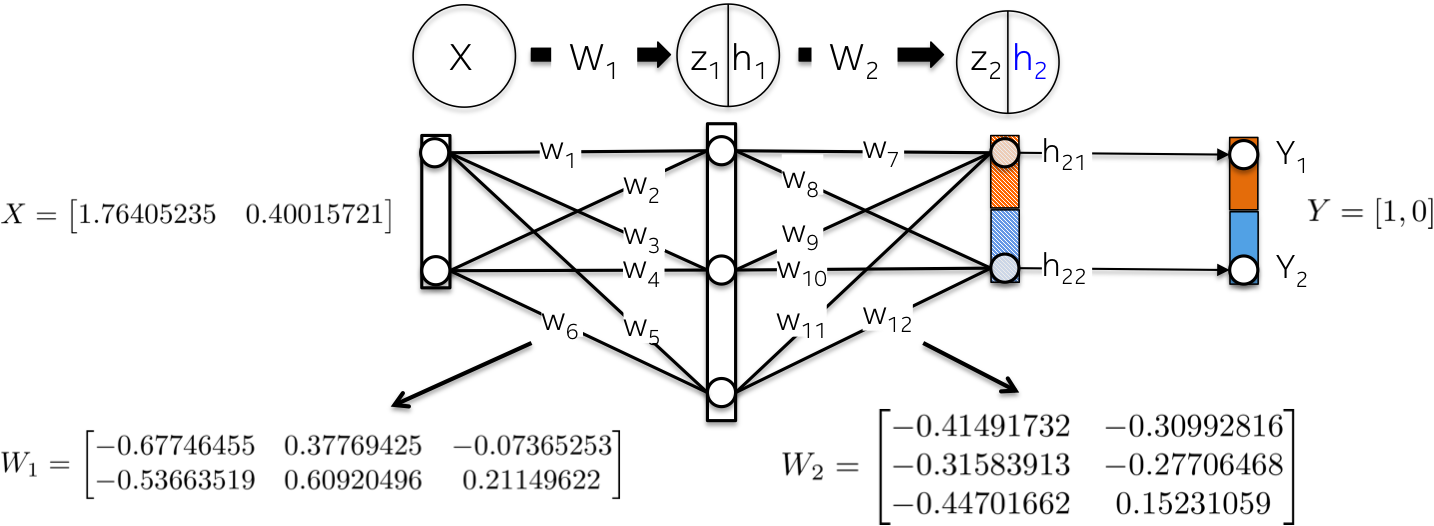
2.2. 前向计算(Forward)
前向计算旨在,计算输入 X 到网络每一层的处理,直到在输出层 h2 得到一个向量.
具体来说,
[1] - 采用权重 W1 作为 kernel,线性映射输入数据 X:

[2] - 采用 Sigmoid 函数缩放加权和 z1,以得到第一个隐藏层 h1 的值. 注:原始的 2D 输入向量已经被映射到 3D 空间.

[3] - 类似的,对于第二个网络层 h2 进行相同处理. 计算第一个隐藏层的加权和 z2,在这里,第一个隐藏层的输出作为第二个网络层的输入.

[4] - 然后,计算 Sigmoid 激活函数. 向量 [0.37166596 0.45414264] 表示网络关于给定输入 X 所计算得到的 log 概率或者预测向量(log probability or predicted vector).

[5] - 计算总损失函数(loss)
损失函数旨在,量化预测向量 h2 和手工标注的 GT y 之间距离.
如:
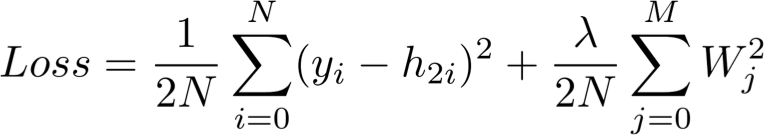
该损失函数包含一个正则参数,用于惩罚较大的权重值. 换句话说,较大的平方权重值会增加损失函数值.
2.3. 反向计算(Backward)
反向计算旨在,更新神经网络的权重,朝着最小化损失函数的方向. 这是一种递归算法(recursive algorithm),其重用了先前计算的梯度,并高度依赖于微分函数.
反向计算首先计算的是损失函数关于输出层权重的偏微分(dLoss/dW2),然后计算关于隐藏层的偏微分(dLoss/dW). 具体如下.
[1] - dLoss/dW2
根据链式法则(chain rule),可以将神经网络的梯度计算进行分解:
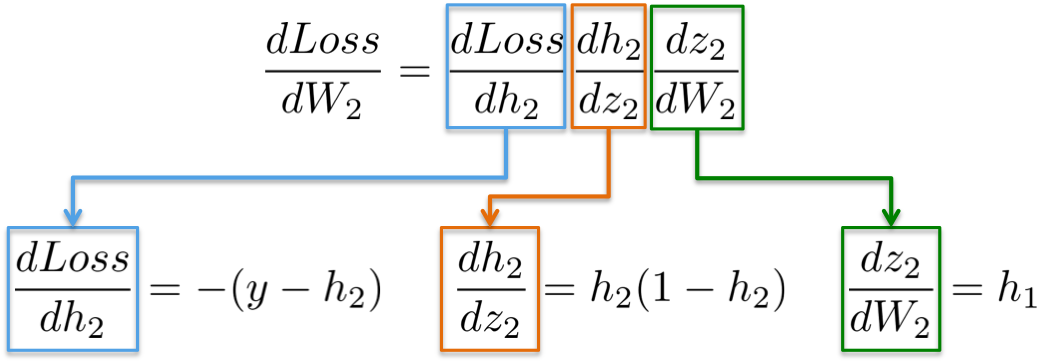
即:
| 函数(Function) | 一阶导数(First derivative) |
|---|---|
| Loss = (y-h2)^2 | dLoss/dW2 = -(y-h2) |
| h2 = Sigmoid(z2) | dh2/dz2 = h2(1-h2) |
| z2 = h1W2 | dz2/dW2 = h1 |
| z2 = h1W2 | dz2/dh1 = W2 |
进一步来说,目的师更新权重W2(蓝色部分),对此需要计算链式中的三个偏微分.

实例化,
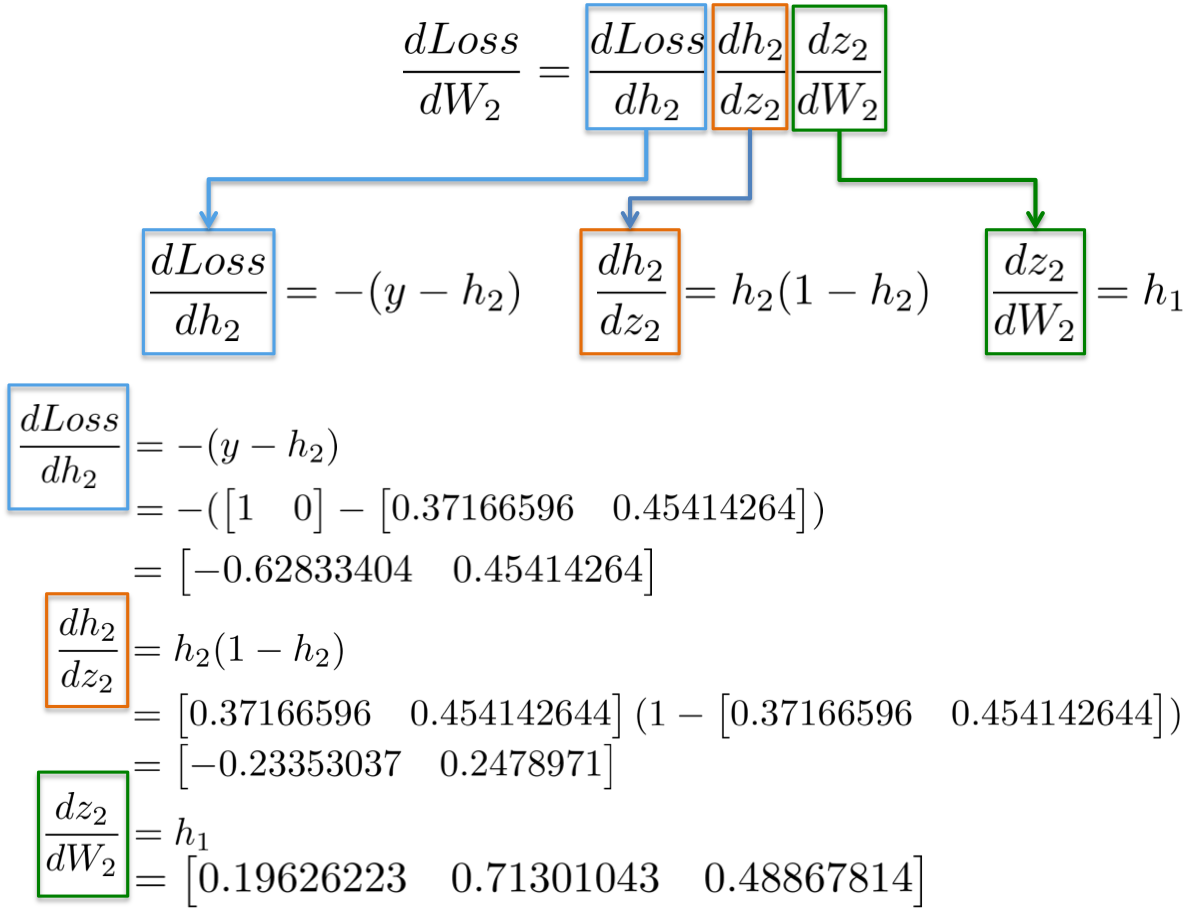
最终可得到 3x2 矩阵 dLoss/dW2,以在最小化损失函数的方向更新原始的 W2 值.
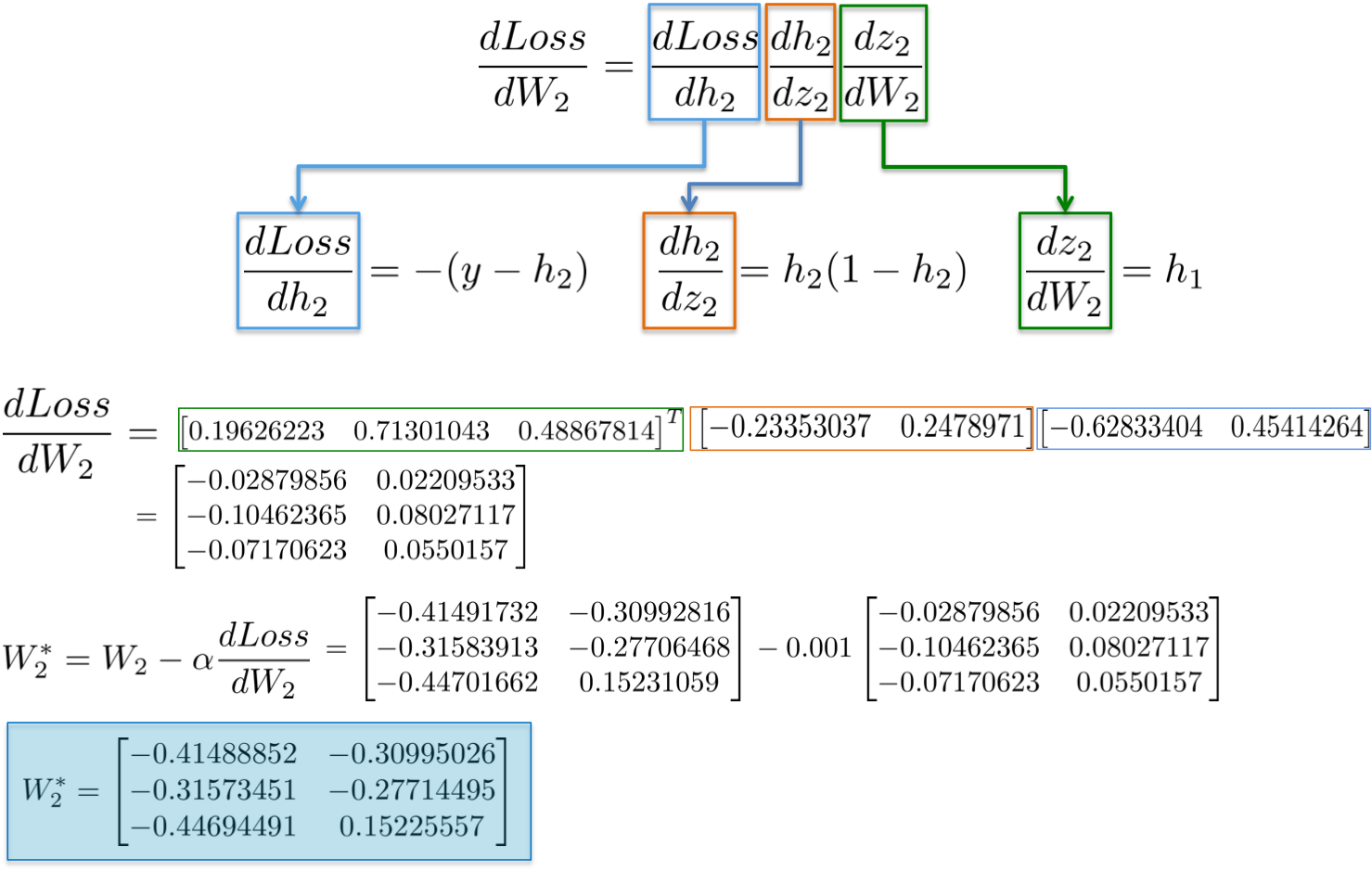
[2] - dLoss/dW1
根据链式法则,更新第一个隐藏层的权重 W1,类似地,
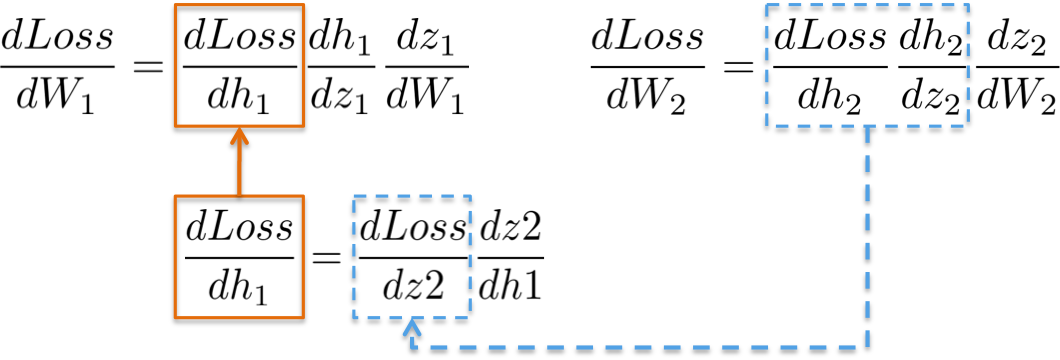
更形象化地,从输出层到权重W1 的路径,会涉及到已经在后面层计算的偏微分:
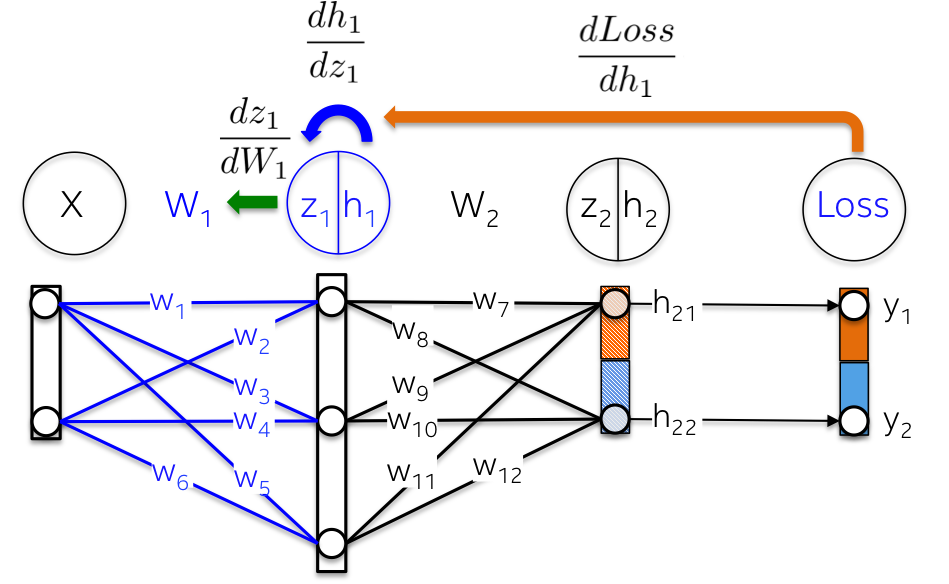
例如,偏微分 dLoss/dh2 和 dLoss /dz2 已经在前面进行了计算,作为学习输出层 dLoss/dW2 权重的依赖项.
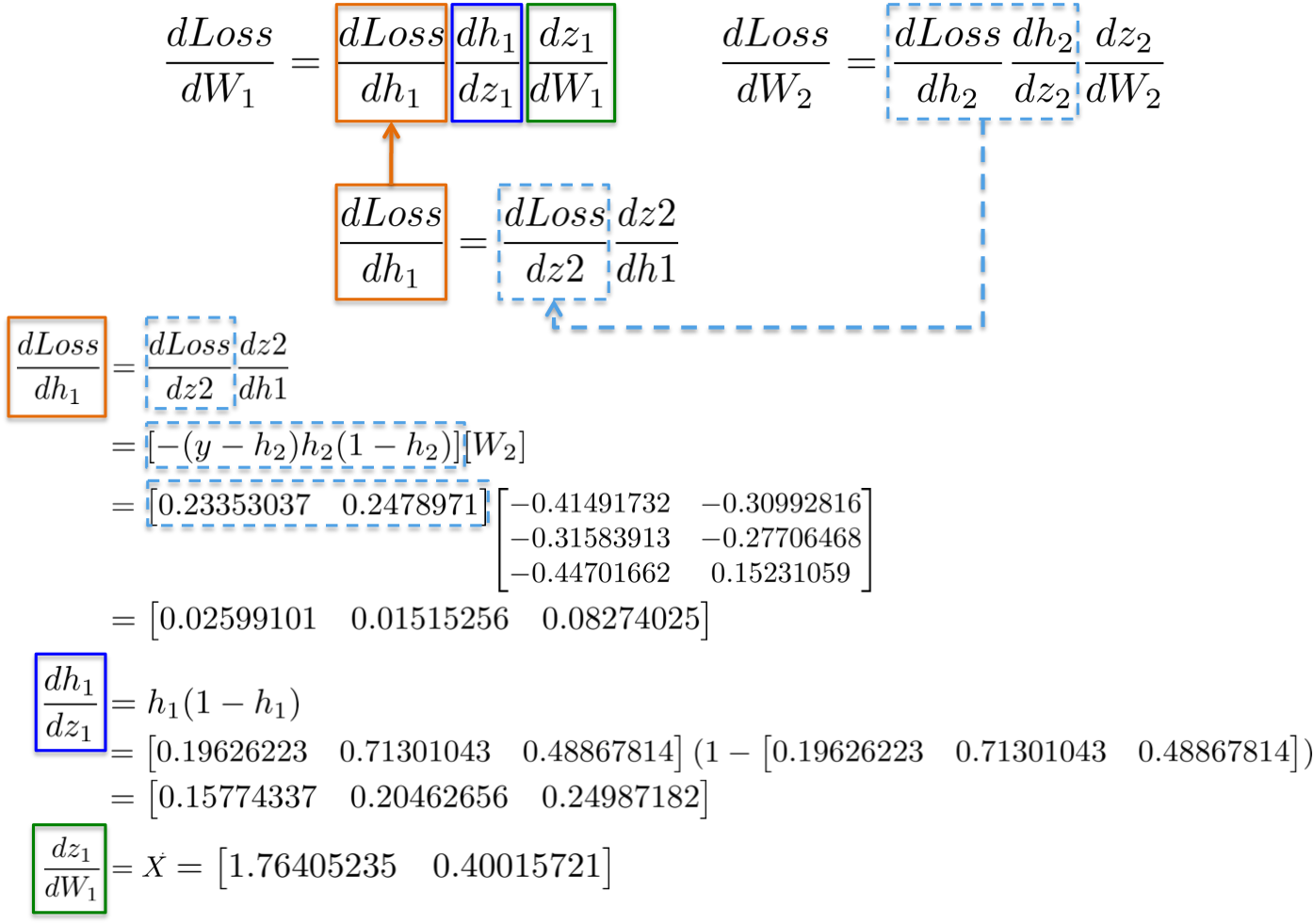
合并所有的偏微分计算,再次根据链式法则,更新隐藏层W1 的权重:
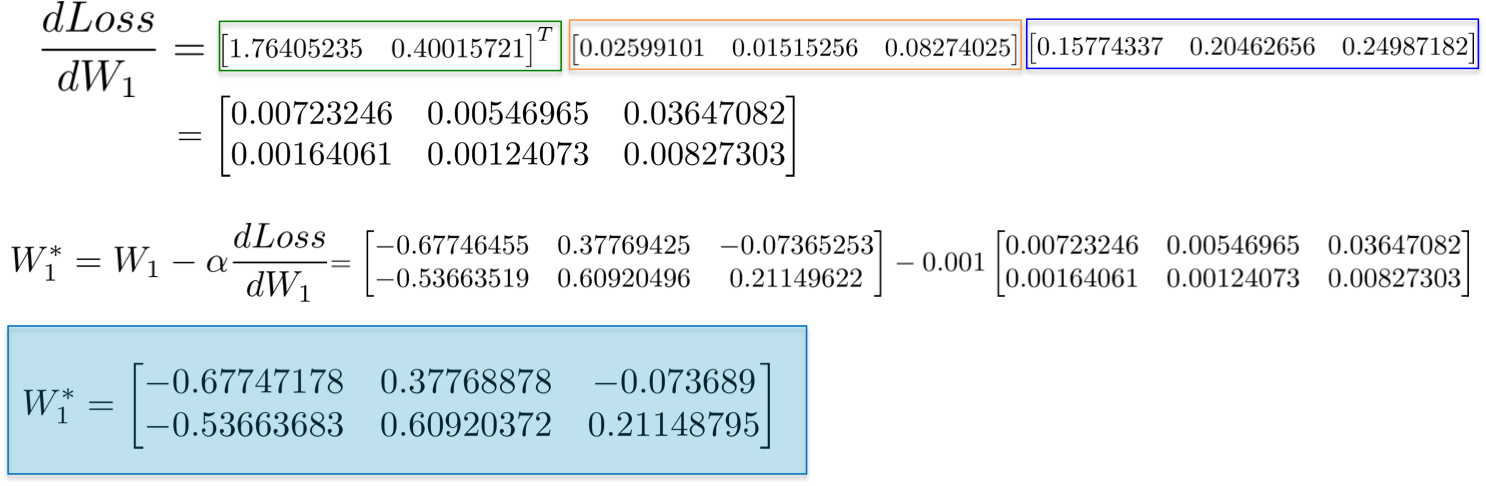
最终,采用在网络训练的一次迭代中新计算得到的值作为新的权重值.
3. Numpy 实现
仅采用 numpy Math 库关于前向神经网络的完整实现,并逐步解释网络的学习过程:
#!/usr/bin/env python
import numpy as np
import ipdb
from scratch_mlp import utils
utils.reset_folders()
def load_XOR_data(N=300):
rng = np.random.RandomState(0)
X = rng.randn(N, 2)
y = np.array(np.logical_xor(X[:, 0] > 0, X[:, 1] > 0), dtype=int)
y = np.expand_dims(y, 1)
y_hot_encoded = []
for x in y:
if x == 0:
y_hot_encoded.append([1,0])
else:
y_hot_encoded.append([0, 1])
return X, np.array(y_hot_encoded)
def sigmoid(z, first_derivative=False):
if first_derivative:
return z*(1.0-z)
return 1.0/(1.0+np.exp(-z))
def tanh(z, first_derivative=True):
if first_derivative:
return (1.0-z*z)
return (1.0-np.exp(-z))/(1.0+np.exp(-z))
def inference(data, weights):
h1 = sigmoid(np.matmul(data, weights[0]))
logits = np.matmul(h1, weights[1])
probs = np.exp(logits)/np.sum(np.exp(logits), axis=1, keepdims=True)
return np.argmax(probs, axis=1)
def run():
#size of minibatch: int(X.shape[0])
N = 50
X, y = load_XOR_data(N=300)
input_dim = int(X.shape[1])
hidden_dim = 10
output_dim = 2
num_epochs = 1000000
learning_rate= 1e-3
reg_coeff = 1e-6
losses = []
accuracies=[]
#--------------------------------------
# Initialize weights:
np.random.seed(2017)
w1 = 2.0*np.random.random((input_dim, hidden_dim))-1.0 #w0=(2,hidden_dim)
w2 = 2.0*np.random.random((hidden_dim, output_dim))-1.0 #w1=(hidden_dim,2)
#Calibratring variances with 1/sqrt(fan_in)
w1 /= np.sqrt(input_dim)
w2 /= np.sqrt(hidden_dim)
for i in range(num_epochs):
index = np.arange(X.shape[0])[:N]
#is want to shuffle indices: np.random.shuffle(index)
#----------------------------------
# Forward step:
h1 = sigmoid(np.matmul(X[index], w1)) #(N, 3)
logits = sigmoid(np.matmul(h1, w2)) #(N, 2)
probs = np.exp(logits)/np.sum(np.exp(logits), axis=1, keepdims=True)
h2 = logits
#-------------------------------------
# Definition of Loss function: mean squared error plus Ridge regularization
L = np.square(y[index]-h2).sum()/(2*N) + reg_coeff*(np.square(w1).sum()+np.square(w2).sum())/(2*N)
losses.append([i,L])
#---------------------------------------
# Backward step: Error = W_l e_l+1 f'_l
# dL/dw2 = dL/dh2 * dh2/dz2 * dz2/dw2
dL_dh2 = -(y[index] - h2) #(N, 2)
dh2_dz2 = sigmoid(h2, first_derivative=True) #(N, 2)
dz2_dw2 = h1 #(N, hidden_dim)
#Gradient for weight2: (hidden_dim,N)x(N,2)*(N,2)
dL_dw2 = dz2_dw2.T.dot(dL_dh2*dh2_dz2) + reg_coeff*np.square(w2).sum()
#dL/dw1 = dL/dh1 * dh1/dz1 * dz1/dw1
# dL/dh1 = dL/dz2 * dz2/dh1
# dL/dz2 = dL/dh2 * dh2/dz2
dL_dz2 = dL_dh2 * dh2_dz2 #(N, 2)
dz2_dh1 = w2 #z2 = h1*w2
dL_dh1 = dL_dz2.dot(dz2_dh1.T) #(N,2)x(2, hidden_dim)=(N, hidden_dim)
dh1_dz1 = sigmoid(h1, first_derivative=True) #(N,hidden_dim)
dz1_dw1 = X[index] #(N,2)
#Gradient for weight1: (2,N)x((N,hidden_dim)*(N,hidden_dim))
dL_dw1 = dz1_dw1.T.dot(dL_dh1*dh1_dz1) + reg_coeff*np.square(w1).sum()
#weight updates:
w2 += -learning_rate*dL_dw2
w1 += -learning_rate*dL_dw1
if True: #(i+1)%1000==0:
y_pred = inference(X, [w1, w2])
y_actual = np.argmax(y, axis=1)
accuracy = np.sum(np.equal(y_pred,y_actual))/len(y_actual)
accuracies.append([i, accuracy])
if (i+1)% 10000 == 0:
print('Epoch %d\tLoss: %f Average L1 error: %f Accuracy: %f' %(i, L, np.mean(np.abs(dL_dh2)), accuracy))
save_filepath = './scratch_mlp/plots/boundary/image_%d.png'%i
text = 'Batch #: %d Accuracy: %.2f Loss value: %.2f'%(i, accuracy, L)
utils.plot_decision_boundary(X, y_actual, lambda x: inference(x, [w1, w2]),
save_filepath=save_filepath, text = text)
save_filepath = './scratch_mlp/plots/loss/image_%d.png' % i
utils.plot_function(losses, save_filepath=save_filepath, ylabel='Loss', title='Loss estimation')
save_filepath = './scratch_mlp/plots/accuracy/image_%d.png' % i
utils.plot_function(accuracies, save_filepath=save_filepath, ylabel='Accuracy', title='Accuracy estimation')
if __name__ == '__main__':
run()分解如图:

3.1. 运行
下面可视化神经网络的训练过程,其通过许多次迭代来逼近 XOR 函数.
[1] - 在隐藏层有 3 个神经元的神经网络,具有较弱的表达能力.
模型学习采用简单的决策边界(decision boundary) 来进行二分类,从直线开始,然后到非线性. 如图:
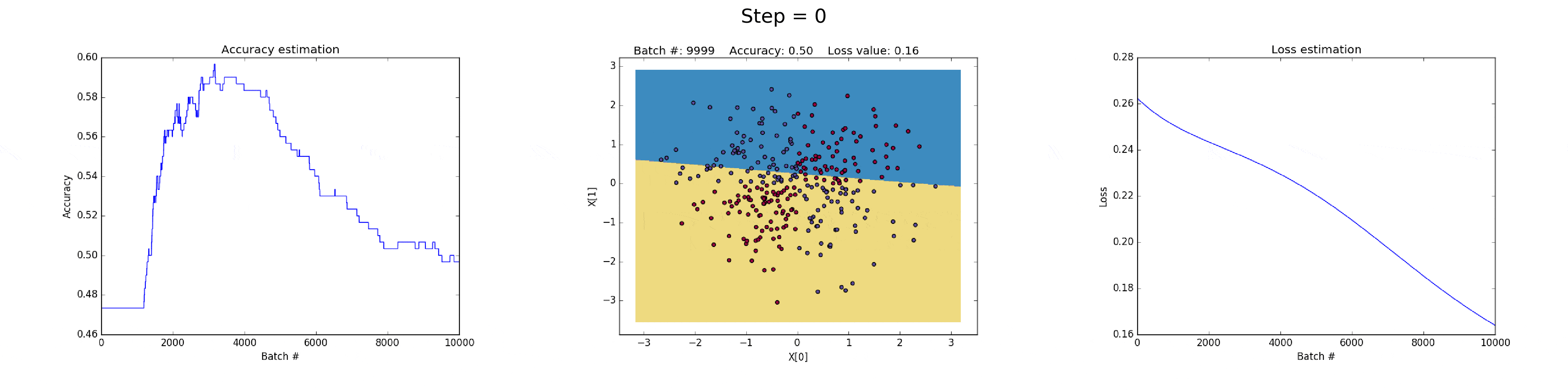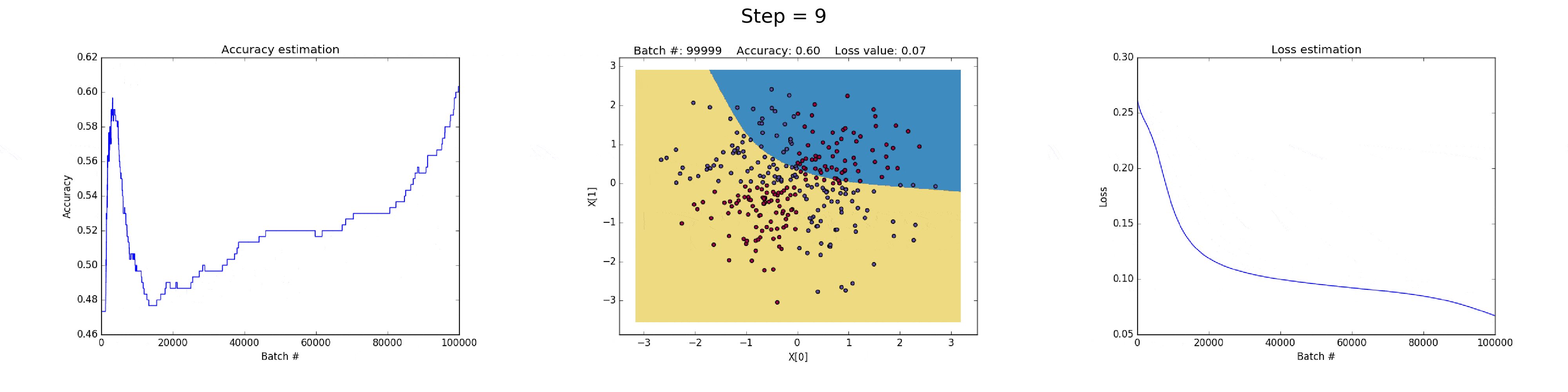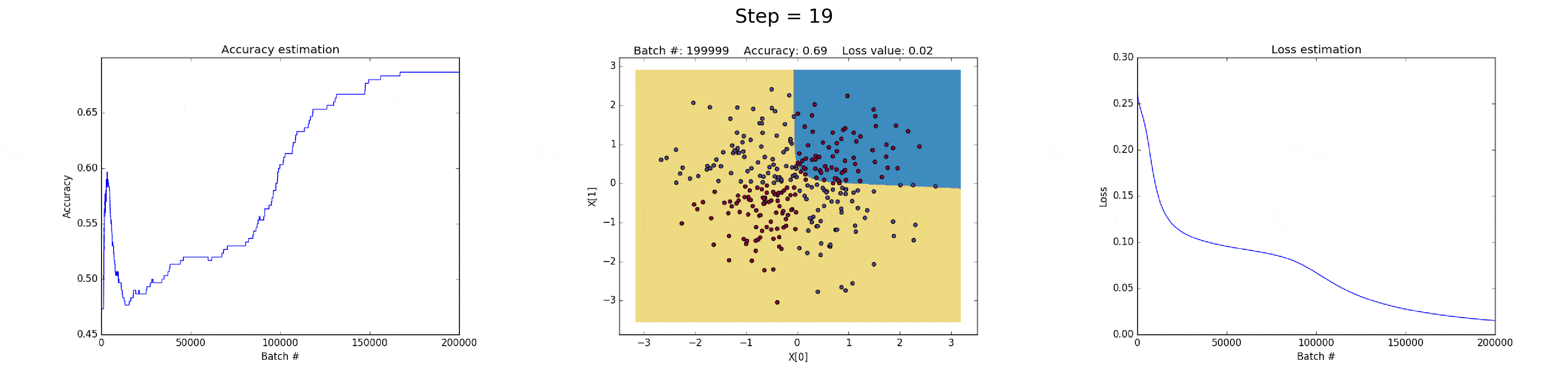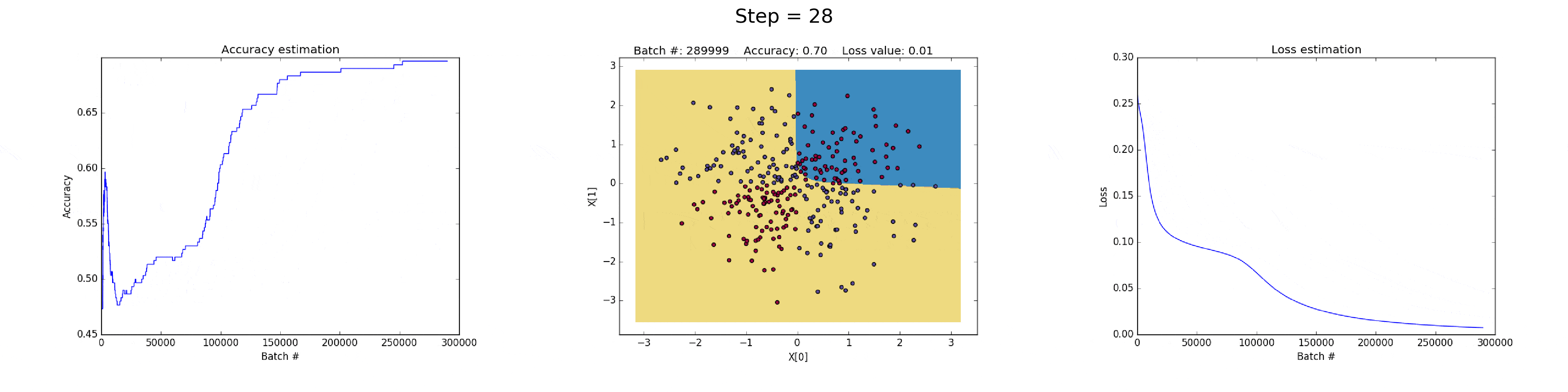
图(all_3neurons_lr_0.003_reg_0.0):(左)Accuracy; (中)学习的决策边界; (右)损失函数
[2] - 在隐藏层有 50 个神经元的神经网络,明显增强了模型的特征表达能力.
模型可以学习更加复杂的决策边界,在可以得到更加精确地结果的同时,还可能会梯度爆炸(exploiting gradients),这也是神经网络训练会遇到的问题.
在BP计算时,如果非常大的梯度乘以权重,则会生成较大的更新的权重值. 这也就是为什么下图训练的最后迭代的时候 loss 值突然增加(step>90).
损失函数的正则化部分,计算了权重的平方值,其本身已经时非常大的值(sum(W^2)/2N).

图(all_50neurons_lr_0.003_reg_0.0001)
这个问题可以通过降低学习率来解决,如下图. 或者,实现一种随着时间减少学习率的策略;或者,采用更强的正则化策略,比如替换 L2 为 L1. 梯度发散和梯度消失时在神经网络中一种有意思的现象.
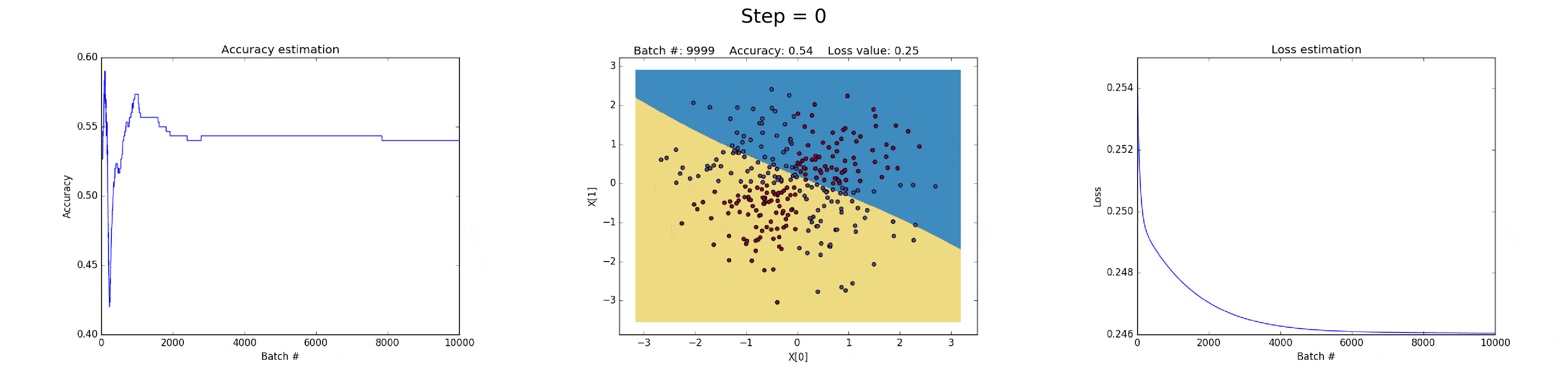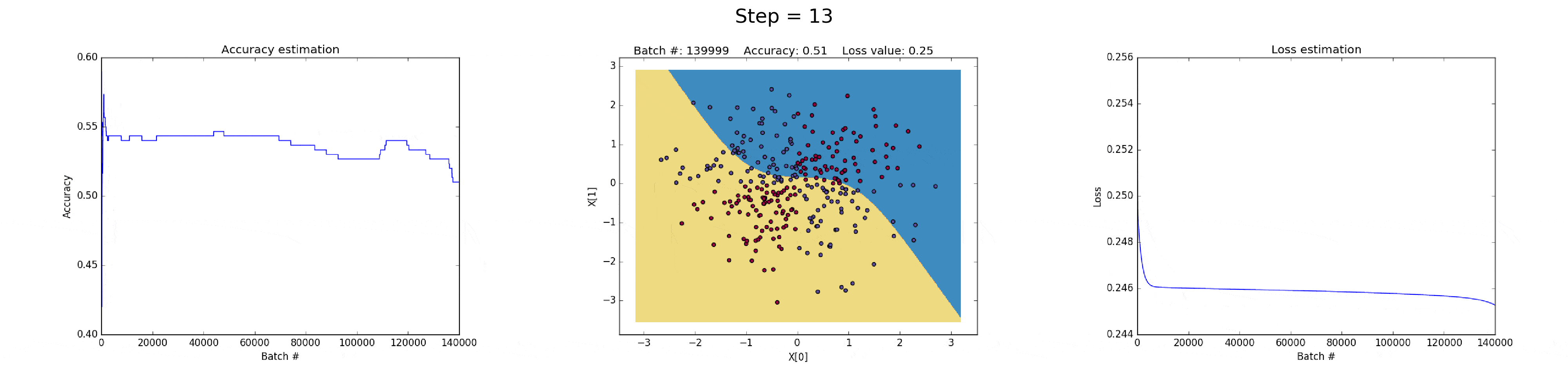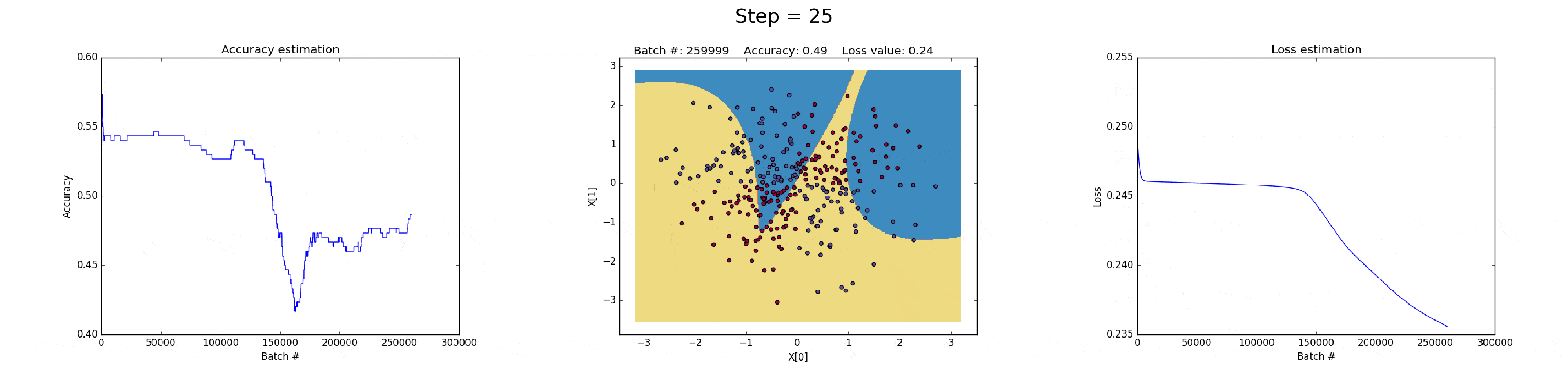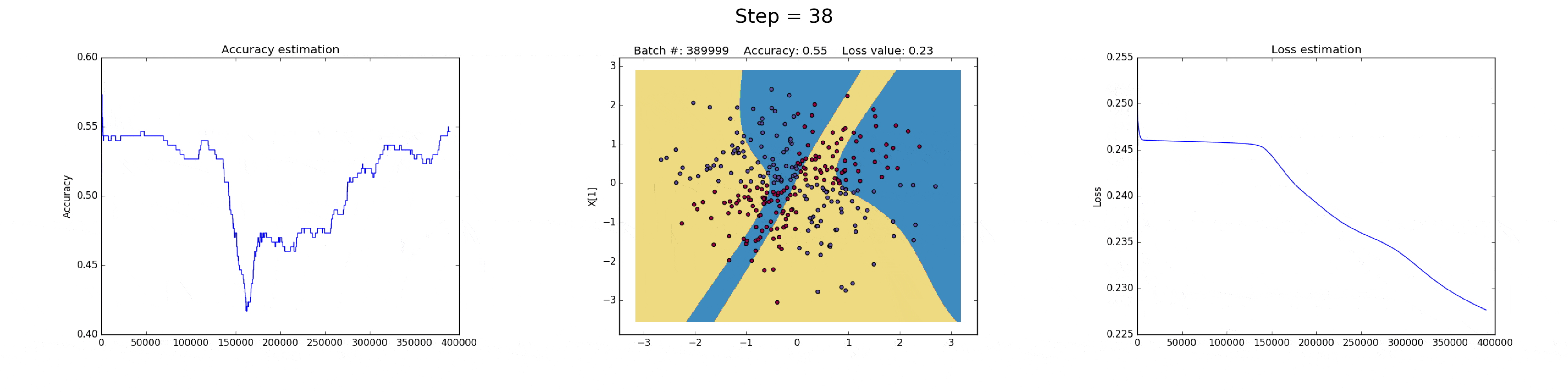
图(all_50neurons_lr_0.003_reg_0.000001).
2 comments
交个朋友 ,兄弟是在 MSR 上海吗:
https://github.com/zyxcambridge
赞!