原文3:反向传播算法推导-全连接神经网络 - 2018.07.06
出处:SIGAI - 微信公众号
1. 为什么需要激活函数
从数学上看,神经网络是一个多层复合函数. 激活函数在很早以前就被引入,其作用是保证神经网络的非线性,因为线性函数无论怎样复合结果还是线性的. 假设神经网络的输入是 n 维向量 x,输出是 m 维向量 y,它实现了如下向量到向量的映射:
$$ R^n \rightarrow R^m $$
我们将这个函数记为:
$$ y = h(x) $$
除输入层之外,标准的前馈型神经网络第 $l$ 层实现的变换可以分为线性组合、激活函数两步. 在某些开源框架中,这两步可能会拆分成不同的层,以利于代码复用和灵活组合. 例如 Caffe 中线性组合由内积层 InnerProductLayer 类实现,激活函数由神经元层NeuronLayer 类实现. 神经网络第层的变换写成矩阵和向量形式为:
$$ \begin{matrix} u^{(l)} = W^{(l)} x^{(l-1)} + b^{(l)} \\ x^{(l)} = f(u^{(l)}) \end{matrix} $$
其中W是权重矩阵,b是偏置向量,u是临时结果,x是神经网络每一层的输出. 激活函数分别作用于向量u的每一个分量,产生一个向量输出x. 在正向传播阶段,反复用上面的公式进行计算,最后得到网络的输出. 对于一个3层的网络,整个映射可以写成:
$$ h(x) = f(W^{(3)} f(W^{(2)} f(W^{(1)}x + b^{(1)}) + b^{(2)}) + b^{(3)}) $$
这是一个3层的复合函数. 从这里可以清晰的看到,如果没有激活函数,整个函数将是一个线性函数:
$$ W^{(3)} (W^{(2)} (W^{(1)}x + b^{(1)}) + b^{(2)}) + b^{(3)} $$
因此对激活函数最基本的要求是必须是非线性的. 在早期,普遍使用的是sigmoid函数和tanh函数. sigmoid函数的计算公式为:
$$ f(x) = \frac{1}{1 + exp(-x)} $$
这个函数的图像为:
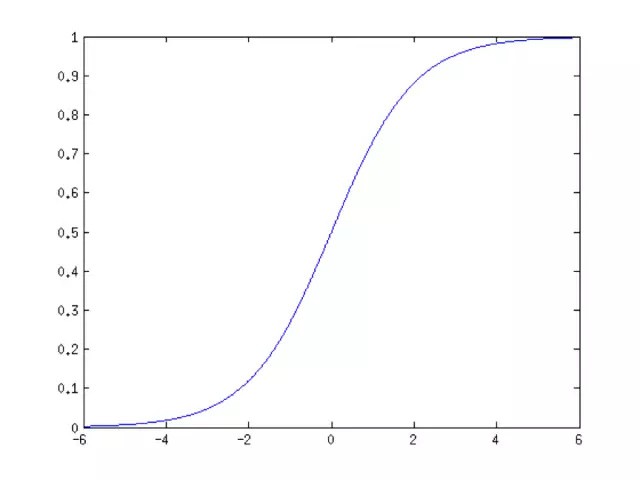
tanh函数的计算公式为:
$$ f(x) = \frac{1 - e^{-2x}}{1 + e^{-2x}} $$
它的图像为:
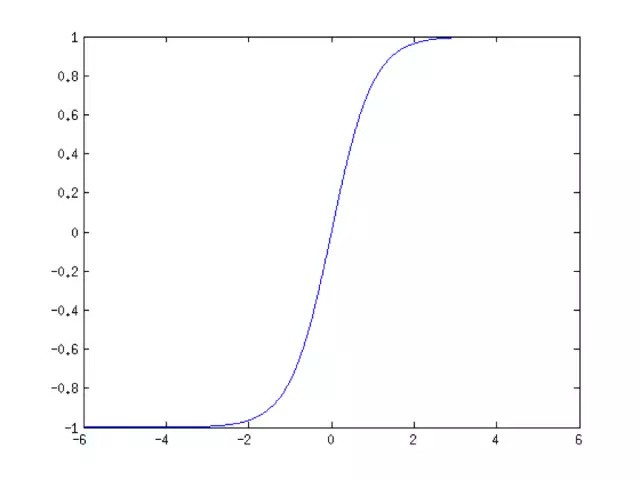
前者的值域为(0,1),单调递增且有界;后者的值域为(-1,+1),是一个中心对称的奇函数,同样也是单调递增且有界.
2. 什么样的函数可以做激活函数
前面已经说过,为保证非线性,激活函数必须为非线性函数,但仅仅具有非线性是不够的. 神经网络在本质上是一个复合函数,这会让我们思考一个问题:这个函数的建模能力有多强?即它能模拟什么样的目标函数?已经证明,只要激活函数选择得当,神经元个数足够多,使用3层即包含一个隐含层的神经网络就可以实现对任何一个从输入向量到输出向量的连续映射函数的逼近,这个结论称为万能逼近(universal approximation)定理. 万能逼近定理的表述为:
如果$\varphi (x)$是一个非常数、有界、单调递增的连续函数,$I_m$ 是 m 维的单位立方体,$I_m$ 中的连续函数空间为 $C(I_m)$. 对于任意 $\epsilon > 0$以及函数$f \in C(I_m)$,存在整数 N,实数$v_i, b_i$,实向量$w_i \in R^m$,通过它们构造函数 $F(x)$作为函数 $f$ 的逼近:
$$ F(\mathbf{x}) = \sum_{i=1}^N v_i \varphi (\mathbf{w}_i^T \mathbf{x} + b_i) $$
对于任意的 $X \in I_m$ 满足:
$$ |F(\mathbf{x}) - f(\mathbf{x})| < \epsilon $$
万能逼近定理的直观解释是可以构造出上面这种形式的函数,逼近定义在单位立方体空间中的任何一个连续函数到任意指定的精度. 这个定理对激活函数的要求是必须非常数、有界、单调递增,并且连续.
文献[1]对使用 sigmoid 激活函数时的情况进行了证明:
如果 $\sigma$ 是一个连续函数,并且满足下面条件:
$$ \begin{matrix} lim_{x \rightarrow -\infty} \sigma(x) = 0 \\ lim_{x \rightarrow +\infty} \sigma(x) = 1 \end{matrix} $$
则,函数族:
$$ f(x) = \sum \alpha_i \sigma(\mathbf{w}_i^T \mathbf{x} + b_i) $$
在空间 n 维单位立方体空间 $C^n[0, 1]$中是稠密的,即,这样的函数可以逼近定义在单位立方体空间中的任意连续函数到任意指定的精度. 显然sigmoid函数就满足对 $\sigma$ 的要求. 上面这些结论的函数输出值都是一个标量,但我们可以把它推广的向量的情况,神经网络的输出一般是一个向量.
只要网络规模设计得当,使用 sigmoid函数 和 ReLU 函数作为激活函数的逼近能力都能够得到保证. ReLU函数定义为:
$$ ReLU(x) = max(0, x) $$
它是一个分段线性函数. 文献7分析了使用ReLU激活函数的神经网络的逼近能力. 下图是一个非线性分类问题的例子,说明了神经网络确实能处理这种非线性问题:
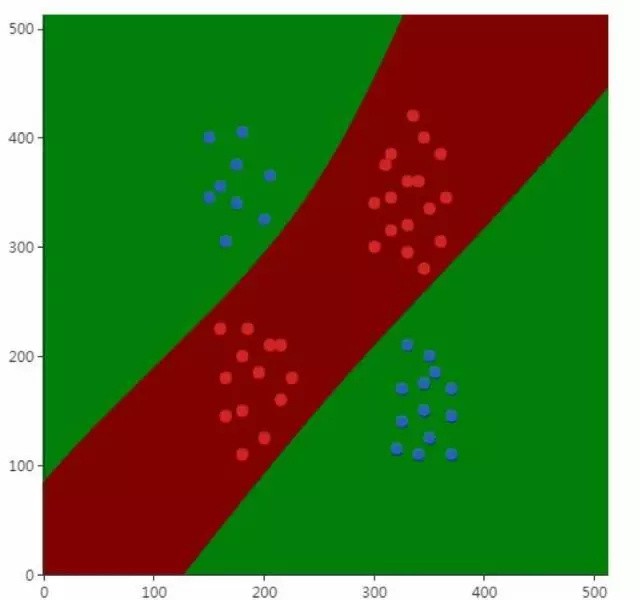
在上图中,用图中的圆圈(红色和蓝色)训练样本训练出来的神经网络模型成功的将蓝色和红色两类样本分开了,分界面是两条曲线.
仅仅满足万能逼近定理的要求也是不够的. 神经网络的训练一般采用反向传播算法+梯度下降法. 反向传播算法从复合函数求导的链式法则导出,因为神经网络是一个多层的复合函数. 在反向传播时,误差项的计算公式为:
$$ \delta^{(l)} = (W^{(l+1)})^T \delta^{(l+1)} \odot f'(u^{(l)}) $$
由于使用梯度下降法需要计算损失函数对参数的梯度值,这个梯度值根据上面的误差项计算,而误差项的计算又涉及到计算激活函数的导数,因此激活函数必须是可导的. 实际应用时并不要求它在定义域内处处可导,只要是几乎处处可导即可. “几乎处处可导”看上去是一个比较有文学味道的词,但实际上是数学中一个严格的概念,这涉及到实变函数的知识. 它的严格定义是这样的:
定义 $R$ 为一维欧式空间,$E \in R$ 是它的一个子集, $mE$ 为点集 $E$ 的 Lebesgue 测度. 如果 $E$ 为 $R$ 中的可测集, $f(x)$ 为定义在 $E$ 的实函数,如果存在 $B \in E$,满足:$mN=0$,对于任意的 $x_0 \in E/N$ 函数 $f(x)$在 $x_0$处都可导,则称$f(x)$在 $E$ 上几乎处处可导.
上面这个定义过于晦涩. 我们可以简单的将几乎处处可导理解成不可导点只有有限个,或者无限可列个(即可用自然数对这些点进行编号,某一区间上的实数就是无限不可列的),即不可导点的测度是0. 可以将测度理解成一维直线的一些点的集合的长度,或者二维平面上一些点的集合的面积. 在概率论中我们知道,连续型随机变量取任何一个点处的值的概率为0,如果将激活函数输入值x看做是随机变量,则它落在这些不可导点处的概率是0. 在计算机实现时,浮点数是进行了离散化的,分成尾数和阶码表示,计算机能表示的浮点数是有限个,因此有一定的概率会落在不可导点处,但概率非常小. ReLU函数在0点处就不可导.
3. 什么样的函数是好的激活函数
反向传播算法计算误差项时每一层都要乘以本层激活函数的导数. 如果激活函数导数的绝对值值小于1,多次连乘之后误差项很快会衰减到接近于0,参数的梯度值由误差项计算得到,从而导致前面层的权重梯度接近于0,参数没有得到有效更新,这称为梯度消失问题. 与之相反的是梯度爆炸问题,如果激活函数导数的绝对大于1,多次乘积之后权重值会趋向于非常大的数,这称为梯度爆炸. 梯度消失问题最早在1991年发现,文献[10]对深层网络难以训练的问题进行了分析,在很长一段时间内,梯度消失问题是困扰神经网络层次加深的一个重要因素.
文献[10]对深层神经网络难以训练的问题进行了理论分析和实验验证. 在实验中,作者训练了有1-5个隐藏层的神经网络,每个隐藏层有1000个神经元,输出层使用 softmax logistic回归函数. 激活函数使用了sigmoid,tanh,以及softsign:
$$ \frac{x}{1 + |x|} $$
权重初始化公式为:
$$ W_{ij} = U[- \frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}] $$
其中,U[a, b]是[a, b]中的均匀分布,n是前一层的尺寸. 理论分析和实验结果都证明,随着网络层数的增加,反向传播的作用越来越小,网络更加难以训练和收敛.
文献[11]中定义了激活函数饱和性的概念,并对各种激活函数进行了分析,给出了改进措施. 如果一个激活函数满足:
$$ \lim\limits_{x \rightarrow + \infty} f'(x)=0 $$
即在正半轴函数的导数趋向于0,则称该函数为右饱和.
类似的如果满足:
$$ \lim\limits_{x \rightarrow -\infty} f'(x)=0 $$
即在负半轴函数的导数趋向于0,则称该函数左饱和.
如果一个激活函数既满足左饱和又满足右饱和,称之为饱和.
如果存在常数c,当x>c时有 $f'(x) = 0$, 则称函数右硬饱和;当x<c时有 $f'(x) = 0$, 则称函数左硬饱和. 既满足左硬饱和又满足右硬饱和的激活函数为硬饱和函数. 饱和性和梯度消失问题密切相关. 在反向传播过程中,误差项在每一层都要乘以激活函数导数值,一旦x的值落入饱和区间,多次乘积之后会导致梯度越来越小,从而出现梯度消失问题.
sigmoid函数的输出映射在(0,1)之间,单调连续,求导容易. 但是由于其软饱和性,容易产生梯度消失,导致训练出现问题;另外它的输出并不是以0为中心的.
tanh函数的输出值以0为中心,位于(-1,+1)区间,相比sigmoid函数训练时收敛速度更快,但它还是饱和函数,存在梯度消失问题.
ReLU函数其形状为一条折线,当x<0时做截断处理. 该函数在0点出不可导,如果忽略这一个点其导数为sgn. 函数的导数计算很简单,而且由于在正半轴导数为1,有效的缓解了梯度消失问题. 在ReLU的基础上又出现了各种新的激活函数,包括ELU、PReLU等. 如果对各种激活函数深入的比较和分析感兴趣,可以阅读文献[11].
4. 常用的激活函数
下表列出了Caffe中支持的激活函数和它们的导数:

5. Caffe 中激活函数的具体实现
下面我们以Caffe为例,介绍这些激活函数的具体实现细节. 在Caffe中,激活函数是一个单独的层,把它和全连接层,卷据层拆开的好处是更为灵活,便于代码复用和组合. 因为无论是全连接层,还是卷据层,它们激活函数的实现是相同的,因此可以用一套代码来完成.
激活函数由神经元层完成,它们的基类是 NeuronLayer,所有的激活函数层均从它派生得到,下面分别进行介绍,限于篇幅,我们只介绍一部分,其他的原理类似. 此外,Dropout机制也由神经元层实现.
5.1. SigmoidLayer
SigmoidLayer类实现了标准sigmoid激活函数. 正向传播函数对每个输入数据计算sigmoid函数值,在这里count是输入数据的维数. 实现代码如下:
sigmoid_layer.cpp
template <typename Dtype>
void SigmoidLayer<Dtype>::Forward_cpu(
const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
// 输入数据
const Dtype* bottom_data = bottom[0]->cpu_data();
// 输出数据
Dtype* top_data = top[0]->mutable_cpu_data();
// 输入数据的个数
const int count = bottom[0]->count();
for (int i = 0; i < count; ++i) {
// 对每个数据计算 sigmoid 函数
top_data[i] = sigmoid(bottom_data[i]);
}
}反向传播函数计算后一层的误差项与激活函数的导数的乘积,实现代码如下:
template <typename Dtype>
void SigmoidLayer<Dtype>::Backward_cpu(
const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down,
const vector<Blob<Dtype>*>& bottom) {
if (propagate_down[0]) {
// top_data 本层的 sigmoid 值
const Dtype* top_data = top[0]->cpu_data();
// top_diff 为后一层的误差
const Dtype* top_diff = top[0]->cpu_diff();
// bottom_diff 保存了本层的误差
Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
const int count = bottom[0]->count();
for (int i = 0; i < count; ++i) {
// sigmoid 函数值在正向传播时被计算出来,
// 并存在这里以供反向传播时使用.
const Dtype sigmoid_x = top_data[i];
// 计算 sigmoid 函数的导数,并与后一层传来的误差相乘.
bottom_diff[i] = top_diff[i] * sigmoid_x * (1. - sigmoid_x);
}
}
}5.2. TanHLayer
TanHLayer类实现了tanh激活函数. 正向传播函数实现代码如下:
tanh_layer.cpp
template <typename Dtype>
void TanHLayer<Dtype>::Forward_cpu(
const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
const Dtype* bottom_data = bottom[0]->cpu_data();
Dtype* top_data = top[0]->mutable_cpu_data();
const int count = bottom[0]->count();
// 对每个输入函数计算 tanh 函数
for (int i = 0; i < count; ++i) {
// 直接调用数学库的 tanh 函数
top_data[i] = tanh(bottom_data[i]);
}
}反向传播函数的实现如下,其中,利用了 tanh 函数的求导公式.
template <typename Dtype>
void TanHLayer<Dtype>::Backward_cpu(
const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down,
const vector<Blob<Dtype>*>& bottom) {
if (propagate_down[0]) {
const Dtype* top_data = top[0]->cpu_data();
const Dtype* top_diff = top[0]->cpu_diff();
Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
const int count = bottom[0]->count();
Dtype tanhx;
for (int i = 0; i < count; ++i) {
tanhx = top_data[i]; // 取得 tanh(x) 的值
// 计算 tanh 的导数,并与后一层的误差相乘.
// 导数计算公式可见上一章节中的表格.
bottom_diff[i] = top_diff[i] * (1 - tanhx * tanhx);
}
}
}5.3. ELULayer
ELULayer类实现ELU激活函数,是直线函数和指数函数的结合.
当 x>0 时函数值为 x;当x<0是一条衰减的指数函数曲线.
可以证明,当 $x \rightarrow -\infty$ 时该函数的极限为-a. 当x<=0时其导数为:
$$ f'(x) = \alpha e^x = \alpha e^x - \alpha + \alpha = \alpha(e^x - 1) + \alpha = f(x) + \alpha $$
这样可以通过函数值得到导数值,减少计算量. 正向传播函数的实现如下:
elu_layer.cpp
template <typename Dtype>
void ELULayer<Dtype>::Forward_cpu(
const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
const Dtype* bottom_data = bottom[0]->cpu_data();
Dtype* top_data = top[0]->mutable_cpu_data();
const int count = bottom[0]->count();
Dtype alpha = this->layer_param_.elu_param().alpha();
for (int i = 0; i < count; ++i) {
// 当 bottom_data[i]>0 时,下时的值为 bottom_data[i];
// 否则,值为 alpha * exp(bottom_data[i] - 1)
top_data[i] = std::max(bottom_data[i], Dtype(0))
+ alpha * (exp(std::min(bottom_data[i], Dtype(0))) - Dtype(1));
}
}反向传播函数的实现如下:
template <typename Dtype>
void ELULayer<Dtype>::Backward_cpu(
const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down,
const vector<Blob<Dtype>*>& bottom) {
if (propagate_down[0]) {
const Dtype* bottom_data = bottom[0]->cpu_data();
const Dtype* top_data = top[0]->cpu_data();
const Dtype* top_diff = top[0]->cpu_diff();
Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
const int count = bottom[0]->count();
Dtype alpha = this->layer_param_.elu_param().alpha();
for (int i = 0; i < count; ++i) {
// 当 x>0 时,下式的值为 top_diff[i];
// 当 x<= 0 时,下式的值为 alpha+top_data[i],即 alpha+f(x)
bottom_diff[i] = top_diff[i] * ((bottom_data[i] > 0)
+ (alpha + top_data[i]) * (bottom_data[i] <= 0));
}
}
}5.4. PReLULayer
类PReLULayer实现了PReLU激活函数. 正向传播函数的实现如下:
prelu_layer.cpp
template <typename Dtype>
void PReLULayer<Dtype>::Forward_cpu(
const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
const Dtype* bottom_data = bottom[0]->cpu_data();
Dtype* top_data = top[0]->mutable_cpu_data();
const int count = bottom[0]->count();
const int dim = bottom[0]->count(2);
const int channels = bottom[0]->channels();
const Dtype* slope_data = this->blobs_[0]->cpu_data();
// For in-place computation
if (bottom[0] == top[0]) {
caffe_copy(count, bottom_data, bottom_memory_.mutable_cpu_data());
}
// if channel_shared, channel index in the following computation becomes always zero.
const int div_factor = channel_shared_ ? channels : 1;
for (int i = 0; i < count; ++i) {
int c = (i / dim) % channels / div_factor;
// 当 bottom_data[i]>0 时,下式的值为 bottom_data[i];
// 否则为 slope_data[c] * bottom_data[i]
top_data[i] = std::max(bottom_data[i], Dtype(0))
+ slope_data[c] * std::min(bottom_data[i], Dtype(0));
}
}反向传播函数的实现如下:
template <typename Dtype>
void PReLULayer<Dtype>::Backward_cpu(
const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down,
const vector<Blob<Dtype>*>& bottom) {
const Dtype* bottom_data = bottom[0]->cpu_data();
const Dtype* slope_data = this->blobs_[0]->cpu_data();
const Dtype* top_diff = top[0]->cpu_diff();
const int count = bottom[0]->count();
const int dim = bottom[0]->count(2);
const int channels = bottom[0]->channels();
// For in-place computation
if (top[0] == bottom[0]) {
bottom_data = bottom_memory_.cpu_data();
}
// if channel_shared, channel index in the following computation becomes always zero.
const int div_factor = channel_shared_ ? channels : 1;
// Propagte to param
// Since to write bottom diff will affect top diff if top and
// bottom blobs are identical (in-place computaion),
// we first compute param backward to keep top_diff unchanged.
if (this->param_propagate_down_[0]) {
Dtype* slope_diff = this->blobs_[0]->mutable_cpu_diff();
for (int i = 0; i < count; ++i) {
int c = (i / dim) % channels / div_factor;
slope_diff[c] += top_diff[i] * bottom_data[i] * (bottom_data[i] <= 0);
}
}
// Propagate to bottom
if (propagate_down[0]) {
Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
for (int i = 0; i < count; ++i) {
int c = (i / dim) % channels / div_factor;
bottom_diff[i] = top_diff[i] * ((bottom_data[i] > 0)
+ slope_data[c] * (bottom_data[i] <= 0));
}
}
}5.5. DropoutLayer
类DropoutLayer实现Dropout机制. 在训练阶段,随机丢掉一部分神经元,用剩下的节点进行前向和后向传播. 这里实现时通过二项分布随机数来控制神经元是否启用,如果随机数取值为1则启用,否则不启用. 正向传播函数的实现如下:
dropout_layer.cpp
template <typename Dtype>
void DropoutLayer<Dtype>::Forward_cpu(
const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
const Dtype* bottom_data = bottom[0]->cpu_data();
Dtype* top_data = top[0]->mutable_cpu_data();
unsigned int* mask = rand_vec_.mutable_cpu_data();
const int count = bottom[0]->count();
if (this->phase_ == TRAIN) { // 训练阶段启用 dropout
// Create random numbers
// 生成随机数,服从伯努利二项分布,随机数存放再掩码数组 mask 中,
// 值为 0 或 1,以 threshold_ 的概率取值 1,
// 以 1.-threshold_ 的概率取值 0.
caffe_rng_bernoulli(count, 1. - threshold_, mask);
for (int i = 0; i < count; ++i) {
// 输出值要么为输入值,即恒等变换;要么为 0.
top_data[i] = bottom_data[i] * mask[i] * scale_;
}
} else {
// 测试阶段,不启用 dropout,直接将输入值原样拷贝输出.
caffe_copy(bottom[0]->count(), bottom_data, top_data);
}
}
反向传播函数的实现如下:
template <typename Dtype>
void DropoutLayer<Dtype>::Backward_cpu(
const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down,
const vector<Blob<Dtype>*>& bottom) {
if (propagate_down[0]) {
const Dtype* top_diff = top[0]->cpu_diff();
Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
if (this->phase_ == TRAIN) {// 训练阶段启用 dropout
// 先获取正向传播时的掩码数组
const unsigned int* mask = rand_vec_.cpu_data();
const int count = bottom[0]->count();
for (int i = 0; i < count; ++i) {
// 导数值要么为 0,要么为输入值.
bottom_diff[i] = top_diff[i] * mask[i] * scale_;
}
} else {// 测试阶段,不启用 dropout
caffe_copy(top[0]->count(), top_diff, bottom_diff);
}
}
}6. 参考文献
[1] Cybenko, G. Approximation by superpositions of a sigmoid function. Mathematics of Control, Signals, and Systems, 2, 303-314, 1989.
[2] Kurt Hornik. Approximation capabilities of multilayer feedforward networks. 1991, Neural Networks.
[3] Hornik, K., Stinchcombe, M., and White, H. Multilayer feedforward networks are universal approximators. Neural Networks, 2, 359-366, 1989.
[4] Hornik, K., Stinchcombe, M., and White, H. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural networks, 3(5), 551-560, 1990.
[5] Leshno, M., Lin, V. Y., Pinkus, A., and Schocken, S. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Networks, 6, 861-867, 1993.
[6] Barron, A. E. Universal approximation bounds for superpositions of a sigmoid function. IEEE Transactions on Information Theory, 39, 930-945, 1993.
[7] Montufar, G. Universal approximation depth and errors of narrow belief networks with discrete units. Neural Computation, 26, 2014.
[8] Raman Arora, Amitabh Basu, Poorya Mianjy, Anirbit Mukherjee. Understanding Deep Neural Networks with Rectified Linear Units. 2016, Electronic Colloquium on Computational Complexity.
[9] Nair, V. and Hinton. Rectified linear units improve restricted Boltzmann machines. In L. Bottou and M. Littman, editors, Proceedings of the Twenty-seventh International Conference on Machine Learning (ICML 2010).
[10] X. Glorot, Y. Bengio. Understanding the difficulty of training deep feedforward neural networks. AISTATS, 2010.
[11] Caglar Gulcehre, Marcin Moczulski, Misha Denil, Yoshua Bengio. Noisy Activation Functions. ICML 2016.