原文 - How to cross-validate PCA, clustering, and matrix decomposition models
机器学习 - 如何交叉验证 PCA、聚类和矩阵分解模型

矩阵分解模型的交叉验证技巧，以 PCA 和聚类为例；并基于 Python 给于说明.

1. 线性回归的交叉验证

交叉验证是现代数据分析中的一种基础范式，普遍用于有监督的设置，如回归和分类. 其处理方式很简单：在数据集 90% 的训练子集上拟合模型，并在剩余的 10% 的测试子集估计模型效果.

然而，对于无监督方法，如降维和聚类等，不能直接应用. 其原因是显而易见的.

以简单的线性回归为例.

${ min_{\pmb{x}} ||\pmb{A} \pmb{x}- \pmb{b}||^2 }$

假设矩阵 ${ A }$，长度为 ${ n }$ 的向量 ${ \pmb{x} }$，长度为 ${ m }$ 的向量 ${ \pmb{b} }$. 模型共有 ${ n }$ 个参数和数据样本. 矩阵 ${ A }$ 的每一行是一个独立的自变量，每个元素为因变量.

交叉验证的基本思想是，留出部分数据样本来估计模型效果.

因此，可以留出矩阵 ${ A }$ 的一些行和向量 ${ \pmb{b} }$ 的对应元素. 保持向量 ${ \pmb{x} }$ 的长度不变. 仍有 ${ n }$ 个待预测变量，但数据样本数 ${ m }$ 变少了.

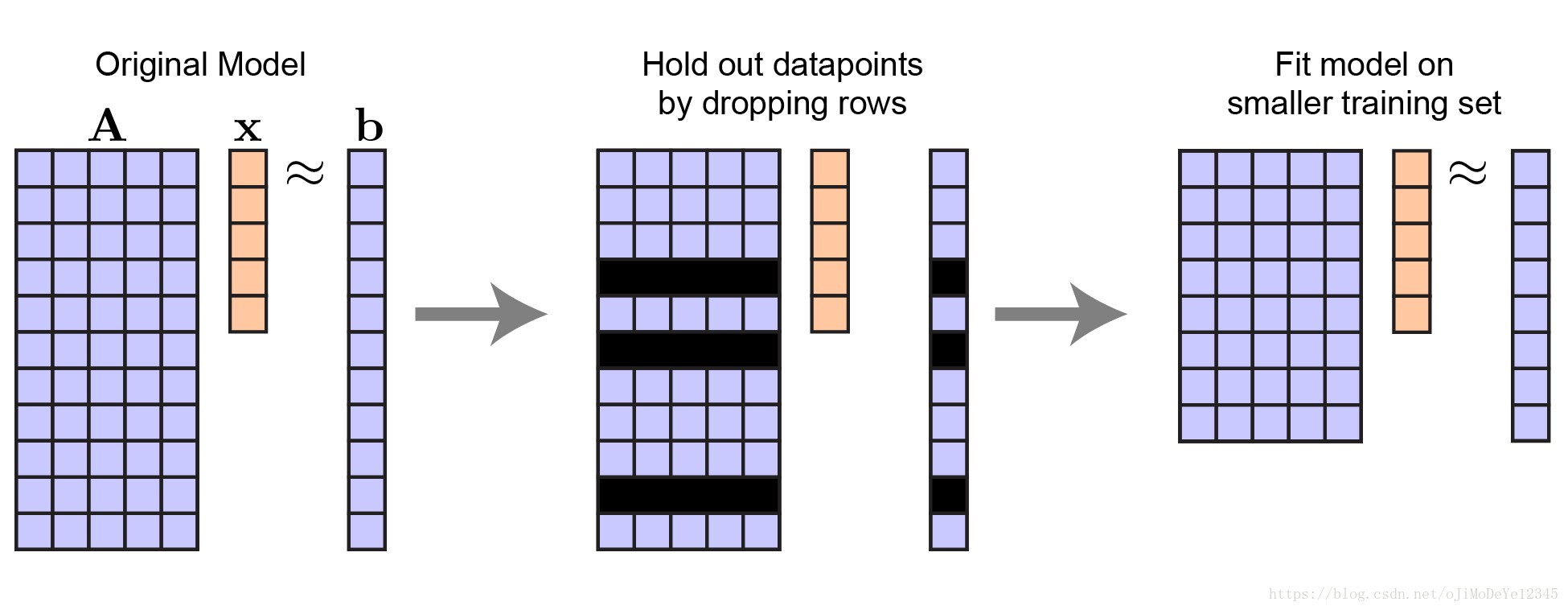
Figure 1. 线性回归中留出数据样本的过程. 向量 ${ \pmb{x} }$ 的长度保持不变.

记：${ A_{tr} }$ 和 ${ \pmb{b}_{tr} }$ 分别为自变量和因变量的训练training数据集. 则，模型拟合等价于：

${ \hat{\pmb{x}} = argmin_{\pmb{x}} || A_{tr} \pmb{x}- \pmb{b}_{tr} ||^2 }$

优化问题是相同的. 采用最小二乘least-squares 等方法即可实现有效优化.

模型拟合后，可以在留出的数据集，如test数据集，以测试模型表现.

根据 ${ ||A_{te} \pmb{x}- \pmb{b}_{te}||^2 }$ 来计算模型的误差.

对于非线性回归问题，也是类似.

对于估计模型何时或计算的泛化误差是否是良好的有很多重要的细节，比如需要对比模型的交叉验证，可以将数据分为三个数据子集：training set、 validation set 和 test set. 如果是基于 test set 选择合适的模型，一般需要有较低的泛化误差. 具体可参考 Elements of Statistical Learning 中的第七章.

2. PCA 的交叉验证

PCA 分解可以看做优化问题：

${ mini_{\pmb{U}, \pmb{V}} || \pmb{U}\pmb{V}^T- \pmb{Y} ||^2 }$

看起来类似于线性回归问题. 区别在于，同时对 ${ A }$ 和 ${ \pmb{x} }$(这里是，${ \pmb{U} }$ 和 ${ \pmb{V}^T }$) 进行优化.

其中，${ \pmb{Y} }$ 是 ${ m×n }$ 的数据矩阵. 在大规模高维数据中，${ m }$ 和 ${ n }$ 的值往往都很大，需要建立其低维线性表示模型. 低维模型是根据 tall-skinny 矩阵 ${ \pmb{U} }$ 和 short-fat 矩阵 ${ \pmb{V} }$ 建立的.

定义矩阵 ${ \pmb{U} }$ 的大小为 ${ m×r }$，矩阵 ${ \pmb{V}^T }$ 的大小为 ${ r×n }$，其中 ${ r<m, r<n }$. 模型估计的矩阵 ${ \pmb{Y} = \pmb{U} \pmb{V}^T }$ 是秩为 ${ r }$ 的矩阵.

以上等式不是真正的 PCA("really PCA")，因为 PCA 还需要矩阵 ${ \pmb{U} }$ 和 ${ \pmb{V} }$ 的每一列具有正交性的约束. 具体可参见:

Everything you did and didn't know about PCA

[Dimensionality Reduction for Matrix- and Tensor-Coded Data [Part 1]](https://cbmm.mit.edu/video/dimensionality-reduction-matrix-and-tensor-coded-data-part-1)

Generalized Low Rank Models - Book

另，对于非负矩阵分解，聚类及许多其它无监督模型也有介绍.类似于PCA分解公式.

PCA 分解图解为：

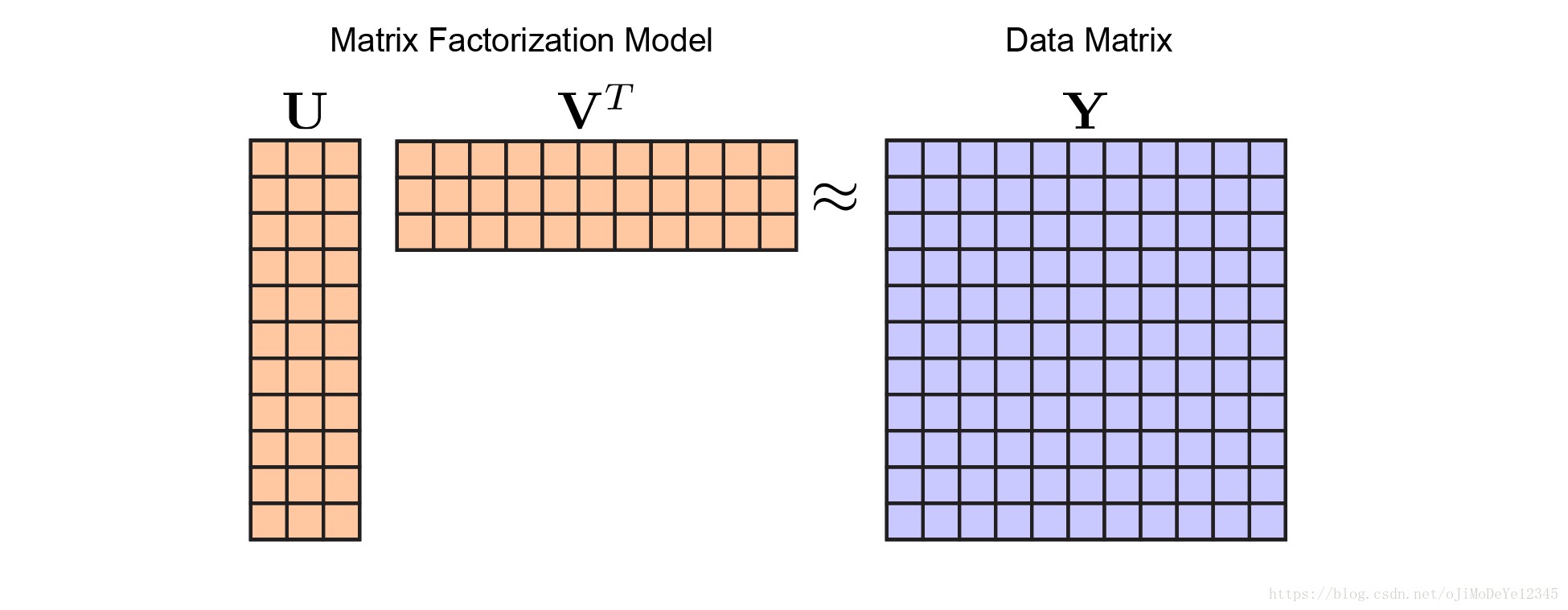
Figure 2. 矩阵分解模型. 不同颜色表示不同的模型参数，矩阵${ \pmb{U} }$ 和 ${ \pmb{V} }$ 为橙色，数据 ${ \pmb{Y} }$ 为蓝色. 通过优化矩阵 ${ \pmb{U} }$ 和 ${ \pmb{V} }$ 来最小化关于 ${ \pmb{Y} }$ 的重构误差.

如何设置合理的留出数据呢？ 如果留出矩阵 ${ \pmb{Y} }$ 的一些行，则必须留出矩阵 ${ \pmb{U} }$ 的对应行. 这就会导致不能拟合模型的全部参数. 同样地，如果留出矩阵 ${ A }$ 的一列，则必须留出矩阵 ${ \pmb{V}^T }$ 的对应一列.

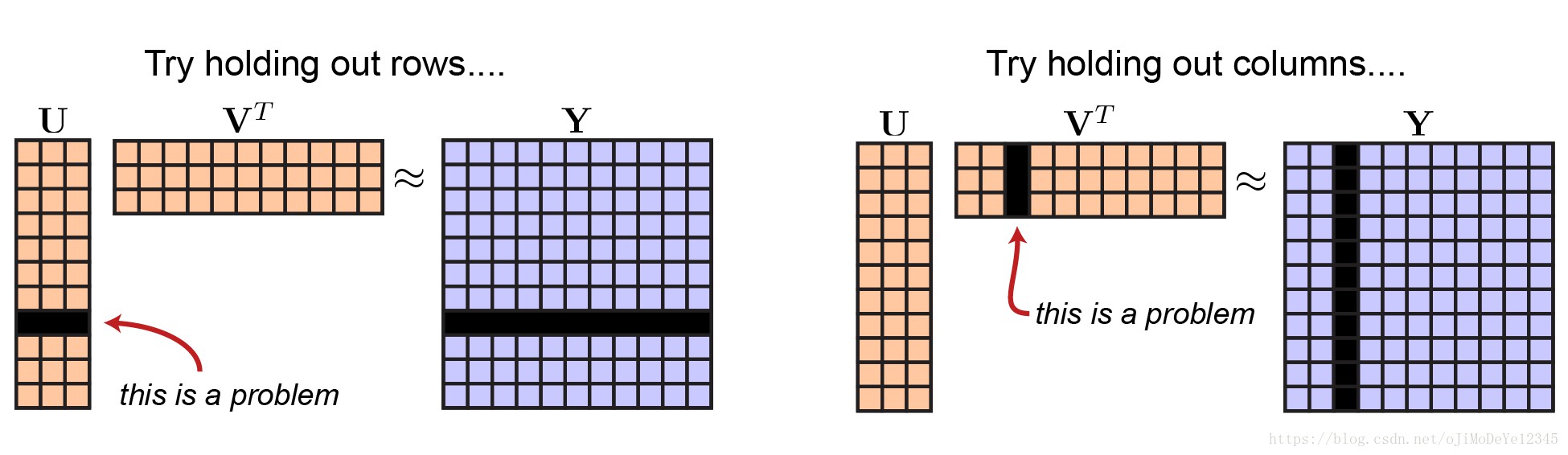
Figure 3. 交叉验证矩阵分解的不完整方案

也许可以只关注对于矩阵 ${ \pmb{V} }$ 的留出数据(测试数据)的误差估计，不关心对于矩阵 ${ \pmb{U} }$ 的交叉验证. 可以采用两步法：

[1] - 留出矩阵 ${ \pmb{Y} }$ 的一些行，然后在训练集上对矩阵 ${ \pmb{U} }$ 的行的子集，来拟合矩阵 ${ \pmb{V} }$.
[2] - 估计矩阵 ${ \pmb{V} }$ 的表现，稍微改变下交叉验证规则，采用测试数据(即留出的行) 来对矩阵 ${ \pmb{U} }$ 估计.

但，这也不是好的方案. 其违反了交叉验证的重要原则 - 不能使用留出数据训练模型参数. 对于矩阵 ${ \pmb{Y} }$ 的估计可能严重过拟合，但通过在测试集上拟合 ${ \pmb{U} }$，将对应的行元素的值设为 0，但对过拟合作用不大. 另外，必须对矩阵 ${ \pmb{U} }$ 留出的行进行拟合，以估计模型在数据矩阵 ${ \pmb{Y} }$ 的对应行上的表现.

相关介绍，可参见：

Cross-validation of component models: A critical look at current methods

Bi-cross-validation of the SVD and the nonnegative matrix factorization

3. PCA 交叉验证的原因

在开始交叉验证之前，首先对交叉验证的重要作用，以及在 PCA 分解中应用的重要性，进行说明.

在回归和其它监督学习方法中，交叉验证的目的是为了监视过拟合和校准参数. 如果有大量的回归参数(如，向量 ${ \pmb{x} }$ 长度非常大时)，通常会添加模型正则项. 这里以 LASSO regression) 为例：

${ min_x ||\pmb{A} \pmb{x}- \pmb{b} ||^2 + \lambda ||\pmb{x}||_1 }$

得到参数估计 ${ \hat{\pmb{x}} }$，其是稀疏的(即，很多元素值都是 0.)

标量参数 ${ \lambda>0 }$ 决定参数估计 ${ \hat{\pmb{x}} }$ 的稀疏性. 如果 ${ \lambda }$ 值太大，则 ${ \hat{\pmb{x}} }$ 非常稀疏，对于预测 ${ \pmb{y} }$ 的表现较差. 如果 ${ \lambda }$ 值太小，则 ${ \hat{\pmb{x}} }$ 基本上不具有稀疏性，且模型可能过拟合.

采用交叉验证可以估计较好的 ${ \lambda }$ 值，即在留出的测试数据上最小化模型误差时的 ${ \lambda }$ 值. 如图：

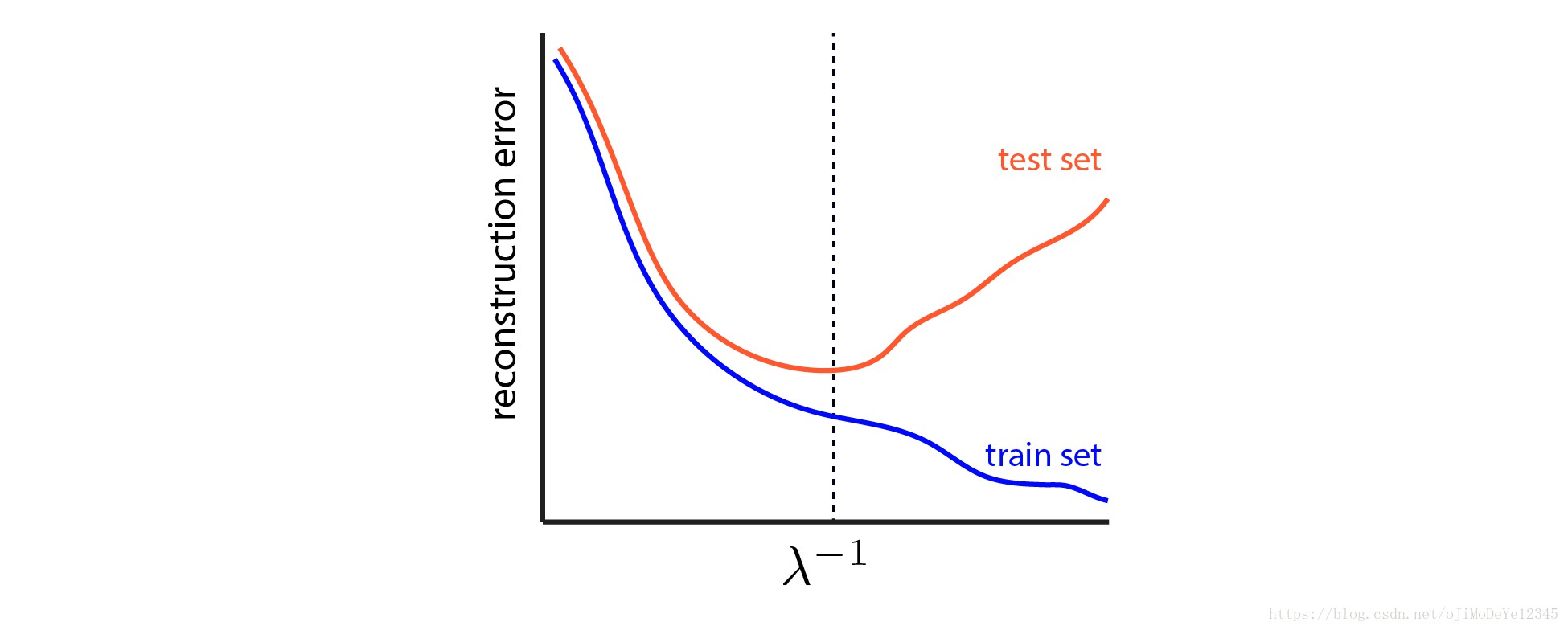
Figure 4. LASSO 的交叉验证图.0 黑色虚线表示最佳的 ${ \lambda }$ 值选择，其能够在留出测试数据集上得到最小的误差.

PCA 还有另一个重要的参数：模型主成分(components)个数.

Automatic choice of dimensionality for PCA

The Optimal Hard Threshold for Singular Values is 4/sqrt(3)

Model averaging and dimension selection for the singular value decomposition

类似的，许多聚类模型需要合适的聚类数作为先验信息.

Determining the number of clusters in a data set

从矩阵分解的角度，它们是相同的问题—— 如，如何选择 ${ r }$，矩阵 ${ \pmb{U} }$ 的宽度 width 和矩阵 ${ \pmb{V}^T }$ 的高度 height.

4. 矩阵分解的交叉验证

如下图，给出了交叉验证在选择 PCA、NMF 和 K-means聚类模型等的主成分数目的作用. 在每个例子中，根据 ${ r=4 }$ 的 groundtruth 模型生成数据并添加噪声. 对于 PCA，PCs 的正确值为 4. 对于 K-means 聚类，聚类中心的正确值为 4. 对于测试误差，所有的模型在当 ${ r>4 }$ 时开始出现过拟合. 只对于训练数据而言，分割点可能不太清晰.

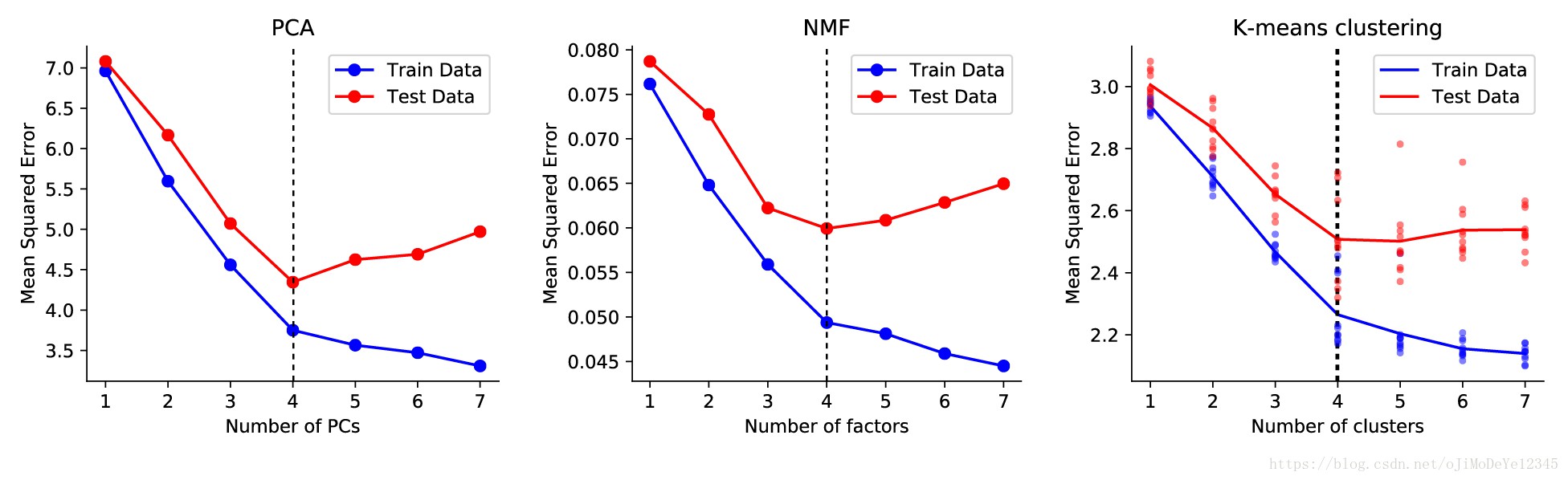
Figure 5. 一些矩阵分解模型的交叉验证图示. 其中，K-means聚类的实现有一点噪声，故进行了多次优化的平均.

代码实现 - cv.py.

随机地缺失数据矩阵 ${ \pmb{Y} }$ 中的一小部分元素：

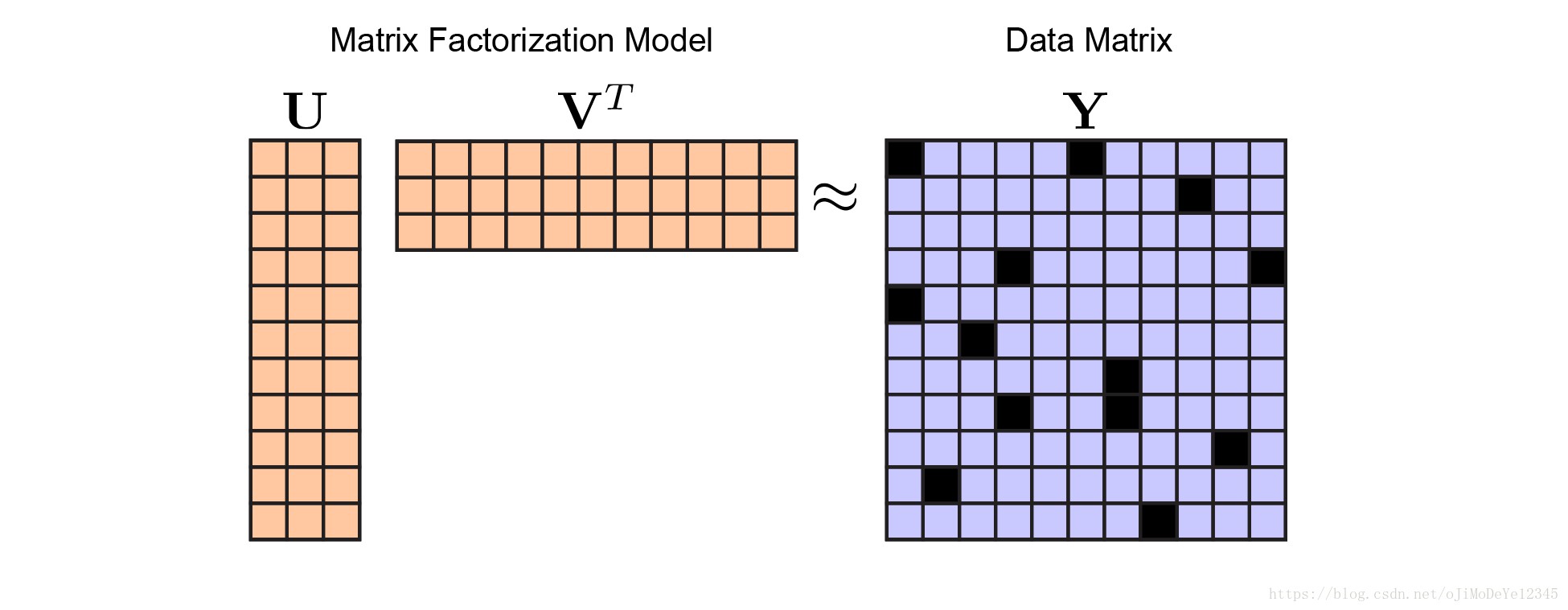
Figure 6. 交叉验证较好的解决方案是随机的留出数据. 重要的是，只要数据矩阵 ${ \pmb{Y} }$ 的中的某一行或某一列没有被完全丢失，则仍然可以学习矩阵 ${ \pmb{U} }$ 和 ${ \pmb{V} }$ 的所有参数. 直观上来说，仍应保持 ${ \pmb{Y} }$ 中每一行或每一列至少有 ${ r }$ 个值.

定义二值矩阵 ${ \pmb{M} }$，作为数据矩阵的掩膜maks. ${ \pmb{M} }$ 中的每个元素值为 0 或 1. ${ m_{ij} = 0 }$ 表示留出(测试)数据，${ m_{ij}=1 }$ 表示训练数据. 即可得到新的优化问题：

${ min_{\pmb{U}, \pmb{V}} ||\pmb{M} \circ (\pmb{U} \pmb{V}^T- \pmb{Y})||_F^2 }$ （3）

其中，${ \circ }$ 为 Hadamard 乘积).

对以上优化问题求解后，即可在留出的测试数据估计模型误差：

${ ||(1- \pmb{M}) \circ (\pmb{U} \pmb{V}^T- \pmb{Y})||_F^2 }$

不必随机的选择 ${ \pmb{M} }$，可以根据实际情况设计需要的留出数据，并保证留出的所有行和所有列具有相同的比例. 详细可见：Cross-Validatory Estimation of the Number of Components in Factor and Principal Components Models

那么，如何求解该优化问题呢？ 等式(3) 是一个低秩矩阵补全问题. 但低秩矩阵补全求解算法中，一般对单个矩阵进行优化，如 ${ \hat{\pmb{Y}} }$，而不是联合优化${ \hat{\pmb{Y}}=\pmb{U}\pmb{V}^T }$(这里想要的.) 如 Exact Matrix Completion via Convex Optimization 中：

${ min_{\hat{\pmb{Y}}} ||\hat{\pmb{Y}}||_* }$

${ s.t. \pmb{M} \circ \hat{\pmb{Y}} = \pmb{M} \circ \pmb{Y} }$

其中，${ || \cdot||_* }$ 表示矩阵的核范数. 最小化矩阵的核范数可以代替直接最小化矩阵 ${ \hat{\pmb{Y}} }$ 的秩，后者计算更复杂.

以上优化等式的优点是，优化问题是凸优化的，具有较好的数学可求解性.

该问题不需要给定矩阵 ${ \pmb{U} }$ 和 ${ \pmb{V} }$，即可求解矩阵补全问题. 但在 PCA 和聚类中，对矩阵 ${ \pmb{U} }$ 和 ${ \pmb{V} }$ 更感兴趣. 且，该方法对于大规模矩阵或张量数据的泛化能力不够好，因为需要对非常大数量的变量 ${ mn }$ 进行优化，而在矩阵因子表示中有 ${ mr + nr }$ 个变量.

矩阵分解一种简单有效的处理方式是，交替最小化算法.

Everything you did and didn't know about PCA

Dimensionality reduction matrix and tensor coded data part1

如 PCA 分解的优化：

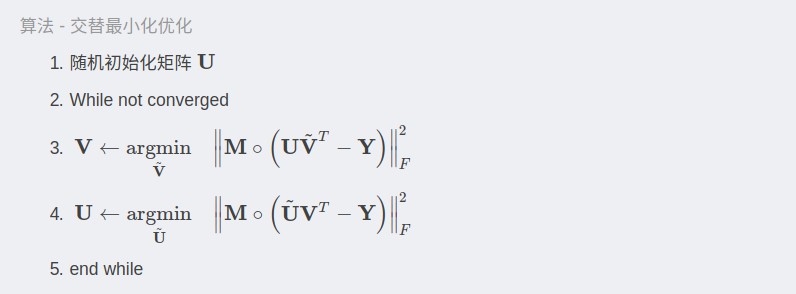
Understanding Alternating Minimization for Matrix Completion 中采用交替最小化来求解矩阵补全问题，但其实现过程仍未完成.

以下给出一些点：

4.1 PCA 实现

在交替最小化优化算法的第 3 行和第 4 行，对每个参数的更新，可以看作是缺失数据的最小二乘问题. 可参考 Solving Least-Squares Regression with Missing Data.

def censored_lstsq(A, B, M):
    """
    Least squares of M * (AX - B) over X, where M is a masking matrix.
    """
    rhs = np.dot(A.T, M * B).T[:,:,None] # n x r x 1 tensor
    T = np.matmul(A.T[None,:,:], M.T[:,:,None] * A[None,:,:])
    return np.linalg.solve(T, rhs).reshape(A.shape[1], B.shape[1])

基于 Numpy，三行代码即可.

交叉验证 PCA 的实现如下：

def cv_pca(data, rank, p_holdout=.1):
    """
    Fit PCA while holding out a fraction of the dataset.
    """
    # create masking matrix
    M = np.random.rand(data.shape)
    
    # fit pca
    U = np.random.randn(data.shape[0], rank)
    for itr in range(20):
        Vt = censored_lstsq(U, data, M)
        U = censored_lstsq(Vt.T, data.T, M.T).T
    
    # We could orthogonalize U and Vt and then rotate to align
    # with directions of maximal variance, but we won't bother.
    
    # return result and test/train error
    resid = np.dot(U, Vt) - data
    train_err = np.mean(resid[M]**2)
    test_err = np.mean(resid[~M]**2)
    return train_err, test_err

需注意：

[1] - 这里简洁起见，没有检查收敛性. 在实际代码中，需要监视重构误差或者 ${ \pmb{U} }$ 和 ${ \pmb{V}^T }$ 的变化情况，当收敛时结束循环.
[2] - censored_1stsq 函数的实现不是最优的. Solving Least-Squares Regression with Missing Data
[3] - 如果数据缺失过多，如一整行或一整列的数据被留出，则由于其是奇异矩阵/不可逆矩阵(singular/non-invertible matrix)，censored——1stsq函数会计算失败.

4.2 NMF 和 K-means 实现

从矩阵分解的角度来说，NMF 十分类似于 PCA. 每个子问题则变成了缺失数据的非负最小二乘问题.

nonnegfac-python 详细实现了非负最小二乘.

另一种方式是基于经典乘法更新规则(multiplicative update rules)进行修改：

修改前：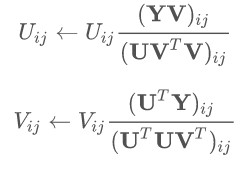

存在缺失数据时，修改后：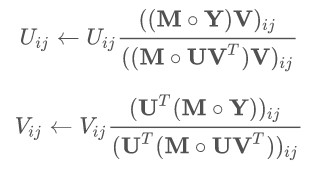

K-means 聚类稍微复杂一点，但基本的交叉验证思想是相同的. 可参见：

缺失数据的 K-means 聚类 - k-POD: A Method for k-Means Clustering of Missing Data
python-scikit-learn-clustering-with-missing-data

5. 总结

交叉验证对于无监督学习也是一种有效方法，这里基于 PCA、NMF 和 K-means 聚类算法进行介绍.

从计算角度，随机留出数据可能导致说明困难. 一个更好的方案是，从数据中留出某些行和列的子集，也就是将数据矩阵分为四部分，如下：

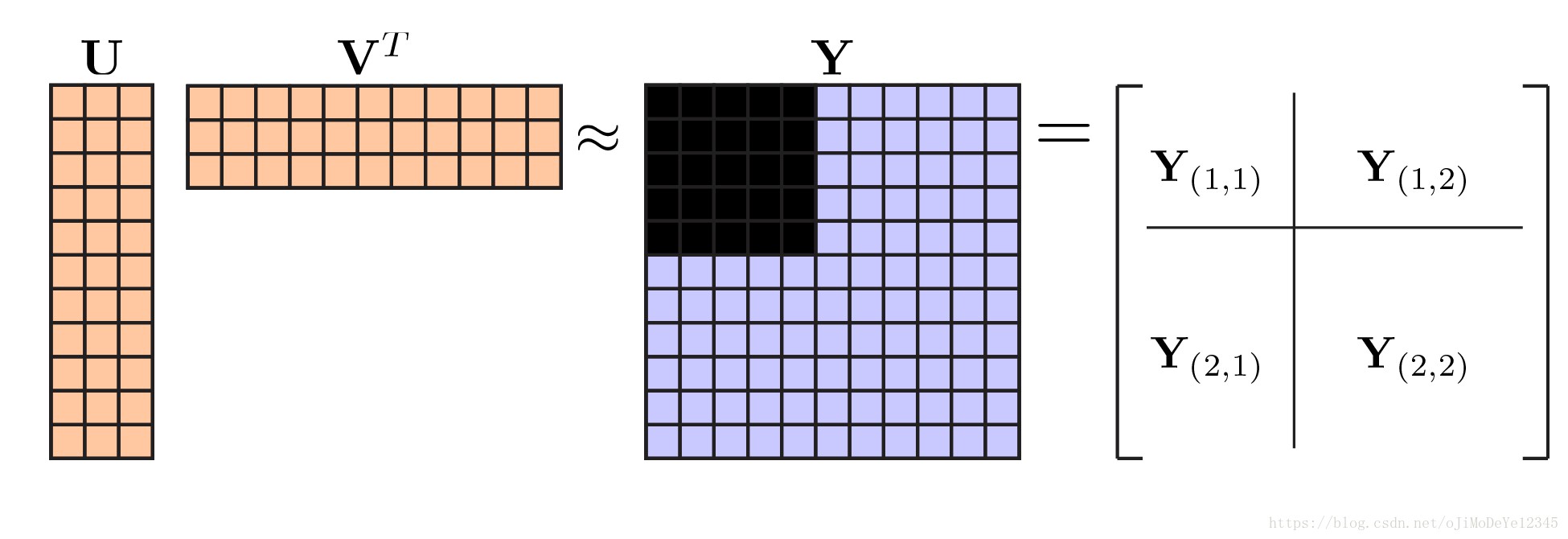
Figure 7. 交叉验证数据留出方法. From Bi-cross-validation of the SVD and the nonnegative matrix factorization

Estimating the number of clusters using cross-validation - K-means 聚类

Cross-Validation for Unsupervised Learning - K-means 聚类，PhD 论文

Cross-validation of component models: A critical look at current methods