线性方程组的一般形式：

$$ Ax = b $$

方程组：

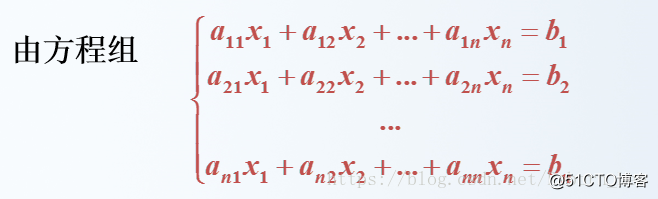
经过变形得到如下形式（变形方程组）：

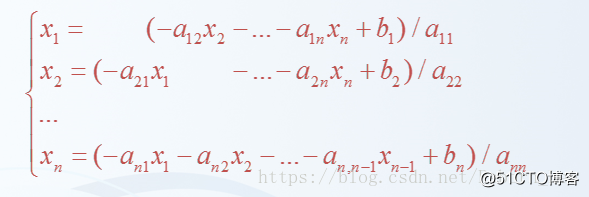
高斯-赛德尔迭代法

Gauss-Seidel迭代求解线性方程组 - 51CTO

得到下面的迭代公式：（仔细看，会发现很妙！）

矩阵形式

首先将矩阵分裂：

收敛问题

实例

如，求解下面的线性方程组得到精确解：

用高斯—赛德尔迭代法求解比较：

将每一步迭代出来的最新结果充分利用，正如上图所说，高斯—赛德尔迭代法认为最新计算出来的分量可能比旧的分量要好些。事实上是否如此，另当别论，这种思想也有其道理。

Python 实现

#!/usr/bin/python3
#!--*--coding:utf-8--*--
import numpy as np

def gauss_seidel_solver(A, b, N):
    x = np.mat(np.zeros((A.shape[0], 1)))
    k = 0
    n = A.shape[0]
    xj = x.copy()
    while k <= N:
        for i in range(n):
            for j in range(n):
                x[i, 0] = (b[i, 0] - A[i, 0:i]*x[0:i, 0] - A[i, i+1:n] * xj[i+1:n, 0])/A[i, i]
                
        if sum(abs(A*x - b)) < 10*-8:
            break
        k = k + 1
        xj = x.copy()
        
    if k == N:
        print('超过最大迭代次数')
    return x


if __name__ == "__main__":
    A = np.mat([[8, -3, 2],
              [4, 11, -1],
              [6, 3, 12]])
    b = np.mat([[20], [33], [36]])

    print(gauss_seidel_solver(A, b, 5))
    '''
    [[3.00001186]
      [2.00000121]
      [0.99999377]]
    '''

雅可比迭代法

雅克比（Jacobi）迭代法求解线性方程组 - 51CTO

一般形式，

雅可比Jacobi 迭代法的一般公式：

矩阵形式