作者:天山老霸王
灰度共生矩阵法(GLCM, Gray-level co-occurrence matrix),就是通过计算灰度图像得到它的共生矩阵,然后透过计算该共生矩阵得到矩阵的部分特征值,来分别代表图像的某些纹理特征(纹理的定义仍是难点)。灰度共生矩阵能反映图像灰度关于方向、相邻间隔、变化幅度等综合信息,它是分析图像的局部模式和它们排列规则的基础。
Python 实现
1. fast_glcm.py
#!--*--coding: utf-8--*--
import numpy as np
import cv2
def fast_glcm(img, vmin=0, vmax=255, nbit=8, kernel_size=5):
mi, ma = vmin, vmax
ks = kernel_size
h,w = img.shape
# digitize
bins = np.linspace(mi, ma+1, nbit+1)
gl1 = np.digitize(img, bins) - 1
gl2 = np.append(gl1[:,1:], gl1[:,-1:], axis=1)
# make glcm
glcm = np.zeros((nbit, nbit, h, w), dtype=np.uint8)
for i in range(nbit):
for j in range(nbit):
mask = ((gl1==i) & (gl2==j))
glcm[i,j, mask] = 1
kernel = np.ones((ks, ks), dtype=np.uint8)
for i in range(nbit):
for j in range(nbit):
glcm[i,j] = cv2.filter2D(glcm[i,j], -1, kernel)
glcm = glcm.astype(np.float32)
return glcm
def fast_glcm_mean(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm mean
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
mean = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
mean += glcm[i,j] * i / (nbit)**2
return mean
def fast_glcm_std(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm std
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
mean = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
mean += glcm[i,j] * i / (nbit)**2
std2 = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
std2 += (glcm[i,j] * i - mean)**2
std = np.sqrt(std2)
return std
def fast_glcm_contrast(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm contrast
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
cont = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
cont += glcm[i,j] * (i-j)**2
return cont
def fast_glcm_dissimilarity(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm dissimilarity
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
diss = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
diss += glcm[i,j] * np.abs(i-j)
return diss
def fast_glcm_homogeneity(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm homogeneity
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
homo = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
homo += glcm[i,j] / (1.+(i-j)**2)
return homo
def fast_glcm_ASM(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm asm, energy
'''
h,w = img.shape
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
asm = np.zeros((h,w), dtype=np.float32)
for i in range(nbit):
for j in range(nbit):
asm += glcm[i,j]**2
ene = np.sqrt(asm)
return asm, ene
def fast_glcm_max(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm max
'''
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
max_ = np.max(glcm, axis=(0,1))
return max_
def fast_glcm_entropy(img, vmin=0, vmax=255, nbit=8, ks=5):
'''
calc glcm entropy
'''
glcm = fast_glcm(img, vmin, vmax, nbit, ks)
pnorm = glcm / np.sum(glcm, axis=(0,1)) + 1./ks**2
ent = np.sum(-pnorm * np.log(pnorm), axis=(0,1))
return ent
if __name__ == '__main__':
from skimage import data
img = data.camera()
h,w = img.shape
img[:,:w//2] = img[:,:w//2]//2+127
nbit = 8
ks = 5
mi, ma = 0, 255
glcm_mean = fast_glcm_mean(img, mi, ma, nbit, ks)2. glcm example
示例如,
#!--*--coding: utf-8--*--
import numpy as np
from skimage import data
from matplotlib import pyplot as plt
import fast_glcm
if __name__ == '__main__':
img = data.camera()
h,w = img.shape
glcm_mean = fast_glcm.fast_glcm_mean(img)
plt.imshow(glcm_mean)
plt.tight_layout()
plt.show()3. plot example
#!--*--coding: utf-8--*--
import numpy as np
from skimage import data
from matplotlib import pyplot as plt
import fast_glcm
from PIL import Image
def main():
pass
if __name__ == '__main__':
img_file = "test.jpg"
img=np.array(Image.open(img_file).convert('L'))
h,w = img.shape
mean = fast_glcm.fast_glcm_mean(img)
std = fast_glcm.fast_glcm_std(img)
cont = fast_glcm.fast_glcm_contrast(img)
diss = fast_glcm.fast_glcm_dissimilarity(img)
homo = fast_glcm.fast_glcm_homogeneity(img)
asm, ene = fast_glcm.fast_glcm_ASM(img)
ma = fast_glcm.fast_glcm_max(img)
ent = fast_glcm.fast_glcm_entropy(img)
plt.figure(figsize=(10,4.5))
fs = 15
plt.subplot(2,5,1)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(img)
plt.title('original', fontsize=fs)
plt.subplot(2,5,2)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(mean)
plt.title('mean', fontsize=fs)
plt.subplot(2,5,3)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(std)
plt.title('std', fontsize=fs)
plt.subplot(2,5,4)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(cont)
plt.title('contrast', fontsize=fs)
plt.subplot(2,5,5)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(diss)
plt.title('dissimilarity', fontsize=fs)
plt.subplot(2,5,6)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(homo)
plt.title('homogeneity', fontsize=fs)
plt.subplot(2,5,7)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(asm)
plt.title('ASM', fontsize=fs)
plt.subplot(2,5,8)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(ene)
plt.title('energy', fontsize=fs)
plt.subplot(2,5,9)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(ma)
plt.title('max', fontsize=fs)
plt.subplot(2,5,10)
plt.tick_params(labelbottom=False, labelleft=False)
plt.imshow(ent)
plt.title('entropy', fontsize=fs)
plt.tight_layout(pad=0.5)
plt.savefig('output.jpg')
plt.show()如,原图:

GLCM 结果图:
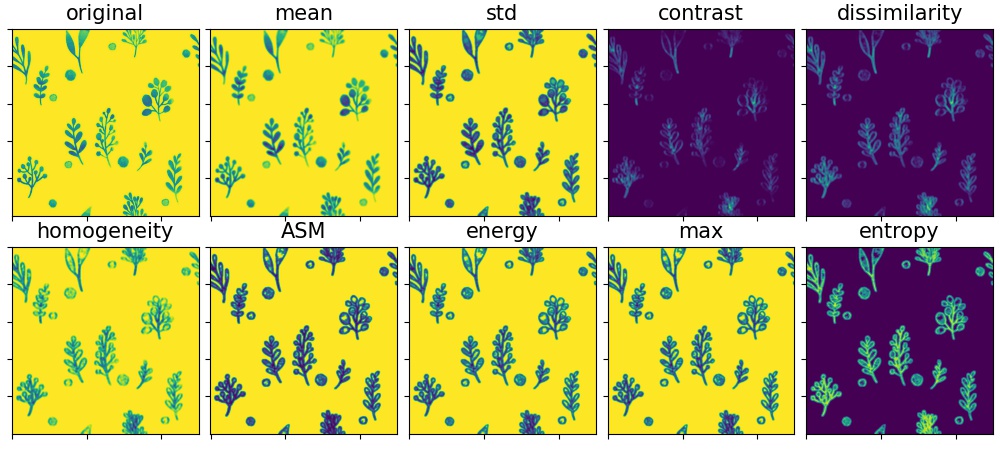
4. 结果含义
[1] - 均值(Mean)
[2] - 标准差(Std)
[3] - 对比度(Contrast)
对比度反应了图像的清晰度和纹理的沟纹深浅。度量矩阵的值是如何分布和图像中局部变化的多少,反应了图像的清晰度和纹理的沟纹深浅。纹理的沟纹越深,反差越大,效果清晰;反之,对比值小,则沟纹浅,效果模糊。
反应某像素值及其领域像素值亮度的对比情况,图像亮度值变化快,换句话说纹理较深,它的对比度就越大,也就是它的纹理越清晰。
[4] - 相异性(Dissimilarity)
计算对比度时,权重随矩阵元素与对角线的距离以指数方式增长,如果改为线性增长,则得到相异性。
[5] - 同质性/逆差距(Homogeneity)
测量图像的局部均匀性,非均匀图像的值较低,均匀图像的值较高。与对比度或相异性相反,同质性的权重随着元素值与对角线的距离而减小,其减小方式是指数形式的。
[6] - 角二阶矩 / 能量( ASM)
灰度共生矩阵( grey level co-occurrence matrix,GLCM)用来描述图像灰度分布的均匀程度和纹理的粗细程度。
如果 GLCM 的所有值都非常接近,则 ASM 值较小; 如果矩阵元素取值差别较大,则 ASM 值较大。当 ASM 值较大时,纹理粗,能量大; 反之,当 ASM 值小时,纹理细,能量小。
$$ ASM = \sum_i \sum_j P(i, j)^2 $$
[7] - 能量(Energy)
是灰度共生矩阵各元素值的平方和,是对图像纹理的灰度变化稳定程度的度量,反应了图像灰度分布均匀程度和纹理粗细度。能量值大表明当前纹理是一种规则变化较为稳定的纹理。更高的值==纹理均匀性。
[8] - 熵(Entropy)
测量图像纹理的随机性(强度分布)。熵是图像包含信息量的随机性度量,表现了图像的复杂程度。当共生矩阵中所有值均相等或者像素值表现出最大的随机性时,熵最大;因此熵值表明了图像灰度分布的复杂程度,熵值越大,图像越复杂。
表示矩阵中元素的分散程度,也表示图像纹理的复杂程度。
[9] - 最大概率(Maximum probability)
表示图像中出现次数最多的纹理特征。