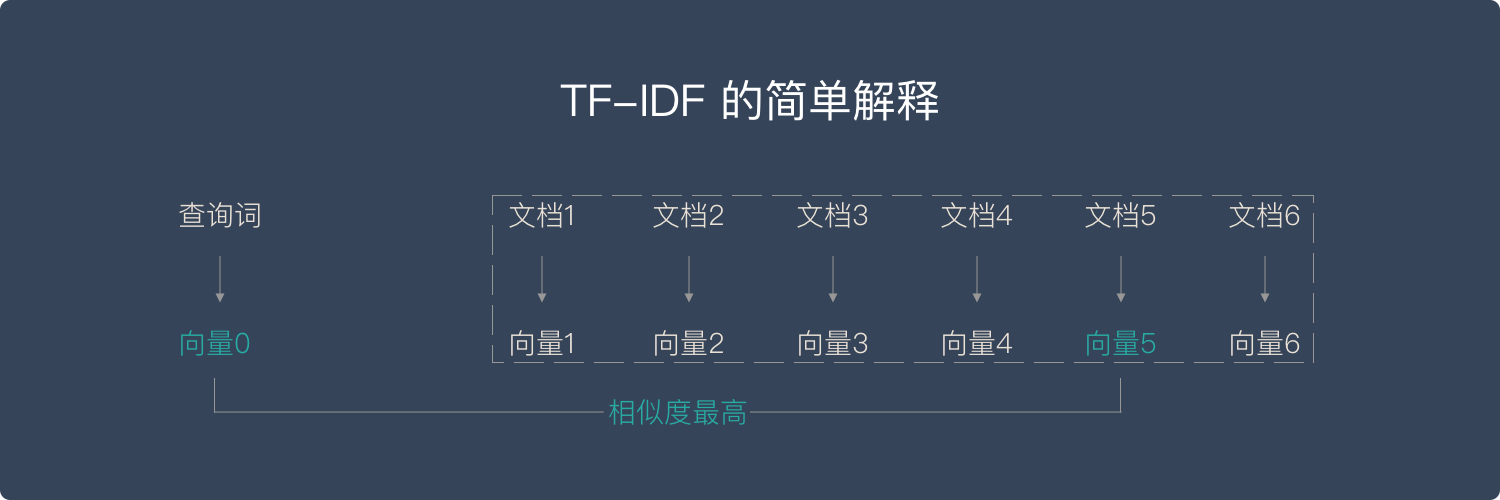
向量空间模型,Vector Space Model,在文本处理中,把对文本内容的处理简化为向量空间中的向量运算,而且其以空间上的相似度来表达语义相似度.
简单来说,向量空间模型就是希望把查询关键字和文档都表达成向量,然后利用向量之间的运算来进一步表达向量间的关系. 比如,一个比较常用的运算就是计算查询关键字所对应的向量和文档所对应的向量之间的 “相关度”.
TF-IDF 算法,Term Frequency-Inverse Document Frequency,用于计算文档之间的相似度.
1. TF - 单词频率
TF 计算一个查询关键字中某一个单词在目标文档中出现的次数.
例如,如果要查询 “Car Insurance”,那么对于每一个文档,都计算“Car” 这个单词在其中出现了多少次,“Insurance”这个单词在其中出现了多少次.
TF 是针对单篇文档而言的,即:某个词在这篇文档中出现了多少次, 而不是某个词在所有文档中出现的次数.
TF 背后的隐含的假设是,查询关键字中的单词应该相对于其他单词更加重要,而文档的重要程度,也就是相关度,与单词在文档中出现的次数成正比. 比如,“Car” 这个单词在文档 A 里出现了 5 次,而在文档 B 里出现了 20 次,那么 TF 计算就认为文档 B 可能更相关.
然而,信息检索中很快就发现,仅有 TF 不能比较完整地描述文档的相关度. 因为语言的因素,有一些单词可能会比较自然地在很多文档中反复出现,比如英语中的 “The”、“An”、“But” 等等. 这些词大多起到了链接语句的作用,是保持语言连贯不可或缺的部分. 然而,如果要搜索 “How to Build A Car” 这个关键词,其中的 “How”、“To” 以及 “A” 都极可能在绝大多数的文档中出现,此时 TF 就无法区分文档的相关度了.
2. IDF - 逆文档频率
基于上述情况,IDF 就应运而生了. 其思路很简单,就是需要去 “惩罚”(Penalize)那些出现在太多文档中的单词.
也就是说,真正携带 “相关” 信息的单词仅仅出现在相对比较少,有时候可能是极少数的文档里. 这个信息,很容易用 “文档频率” 来计算,也就是,有多少文档涵盖了这个单词. 很明显,如果有太多文档都涵盖了某个单词,这个单词也就越不重要,或者说是这个单词就越没有信息量. 因此,需要对 TF 的值进行修正,而 IDF 的想法是用 DF 的倒数来进行修正. 倒数的应用正好表达了这样的思想,DF 值越大越不重要.
3. TF-IDF 计算
TF-IDF 计算:
[1] - 计算 TF:
$$ TF = \frac{某个单词在文档中出现的次数}{文档的总词数} $$
[2] - 计算 IDF:
$$ IDF = log(\frac{文档集合中的文档总数}{包含该单词的文档数 + 1}) $$
[3] - 计算 TF-IDF,将 TF 值乘以 IDF 值,如:
$$ \text{TF-IDF} = TF * IDF $$
TF-IDF 算法主要适用于英文,中文首先要分词,分词后要解决多词一义,以及一词多义问题,这两个问题通过简单的 TF-IDF 方法不能很好的解决.
于是就有了后来的词嵌入方法,用向量来表征一个词.
4. TF-IDF 实现
Python 计算如:
features = np.zeros((numDocs, numWords), "float32")
for idx in range(0, numDocs):
words = extract_words(Docs[idx])
for w in words:
#单篇文档单词出现频次统计
features[idx][w] += 1
#TF-IDF计算
nbr_occurences = np.sum((features > 0) * 1, axis = 0)
idf = np.array(np.log((1.0*numDocs+1) / (1.0*nbr_occurences + 1)), 'float32')
tf_idf = features*idf基于 Scikit-learn 库 text-feature-extraction 的实现:
from sklearn.feature_extraction.text import CountVectorizer
#示例语料
corpus = ['This is the first document.',
'This is the second second document.',
'And the third one.',
'Is this the first document?']
#将文本中的词语转换为词频矩阵
vectorizer = CountVectorizer()
#计算某个单词出现的次数
X = vectorizer.fit_transform(corpus)
#获取词袋中所有文本关键词
words = vectorizer.get_feature_names()
print(words)
#['and', 'document', 'first', 'is', 'one', 'second', 'the', 'third', 'this']
#查看词频结果
print(X.toarray())
#array([[0, 1, 1, 1, 0, 0, 1, 0, 1],
# [0, 1, 0, 1, 0, 2, 1, 0, 1],
# [1, 0, 0, 0, 1, 0, 1, 1, 0],
# [0, 1, 1, 1, 0, 0, 1, 0, 1]])
#
from sklearn.feature_extraction.text import TfidfTransformer
transformer = TfidfTransformer(smooth_idf=False)
#将词频矩阵X统计成TF-IDF值
tfidf = transformer.fit_transform(X)
#tfidf[i][j]表示i类文本中的tf-idf权重
weights = tfidf.toarray()
print(weights)
#array([[0. , 0.43306685, 0.56943086, 0.43306685, 0. ,
# 0. , 0.33631504, 0. , 0.43306685],
# [0. , 0.24014568, 0. , 0.24014568, 0. ,
# 0.89006176, 0.18649454, 0. , 0.24014568],
# [0.56115953, 0. , 0. , 0. , 0.56115953,
# 0. , 0.23515939, 0.56115953, 0. ],
# [0. , 0.43306685, 0.56943086, 0.43306685, 0. ,
# 0. , 0.33631504, 0. , 0.43306685]])
#打印每类文本的tf-idf词语权重
for idx in range(len(weights)):
for jdx in range(len(words)):
print('[INFO]{}th Doc - Word: {} - Weights: {}'.format(idx, words[jdx],weights[idx][jdx])) 5. TF-IDF 变形

5.1. 变形1 - 通过对数函数避免 TF 线性增长
很多人注意到 TF 的值在原始的定义中没有任何上限. 虽然一般认为一个文档包含查询关键词多次相对来说表达了某种相关度,但这样的关系很难说是线性的. 拿刚才举过的关于 “Car Insurance” 的例子来说,文档 A 可能包含 “Car” 这个词 100 次,而文档 B 可能包含 200 次,是不是说文档 B 的相关度就是文档 A 的 2 倍呢?其实,很多人意识到,超过了某个阈值之后,这个 TF 也就没那么有区分度了.
用 Log,也就是对数函数,对 TF 进行变换,就是一个不让 TF 线性增长的技巧. 具体来说,人们常常用 1+Log(TF) 这个值来代替原来的 TF 取值. 在这样新的计算下,假设 “Car” 出现一次,新的值是 1,出现 100 次,新的值是 5.6,而出现 200 次,新的值是 6.3. 很明显,这样的计算保持了一个平衡,既有区分度,但也不至于完全线性增长.
5.2. 变形2 - 标准化解决长文档、短文档问题
经典的计算并没有考虑 “长文档” 和“短文档”的区别. 一个文档 A 有 3,000 个单词,一个文档 B 有 250 个单词,很明显,即便 “Car” 在这两个文档中都同样出现过 20 次,也不能说这两个文档都同等相关. 对 TF 进行 “标准化”(Normalization),特别是根据文档的最大 TF 值进行的标准化,成了另外一个比较常用的技巧.
5.3. 变形3 - 对数函数处理 IDF
第三个常用的技巧,也是利用了对数函数进行变换的,是对 IDF 进行处理. 相对于直接使用 IDF 来作为 “惩罚因素”,我们可以使用 N+1 然后除以 DF 作为一个新的 DF 的倒数,并且再在这个基础上通过一个对数变化. 这里的 N 是所有文档的总数. 这样做的好处就是,第一,使用了文档总数来做标准化,很类似上面提到的标准化的思路;第二,利用对数来达到非线性增长的目的.
5.4. 变形4 - 查询词及文档向量标准化
还有一个重要的 TF-IDF 变种,则是对查询关键字向量,以及文档向量进行标准化,使得这些向量能够不受向量里有效元素多少的影响,也就是不同的文档可能有不同的长度. 在线性代数里,可以把向量都标准化为一个单位向量的长度. 这个时候再进行点积运算,就相当于在原来的向量上进行余弦相似度的运算. 所以,另外一个角度利用这个规则就是直接在多数时候进行余弦相似度运算,以代替点积运算.