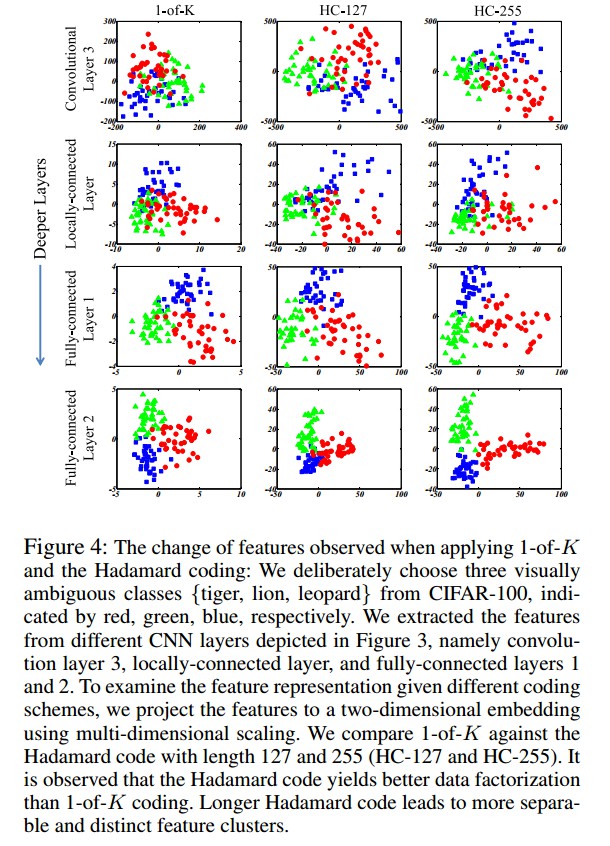
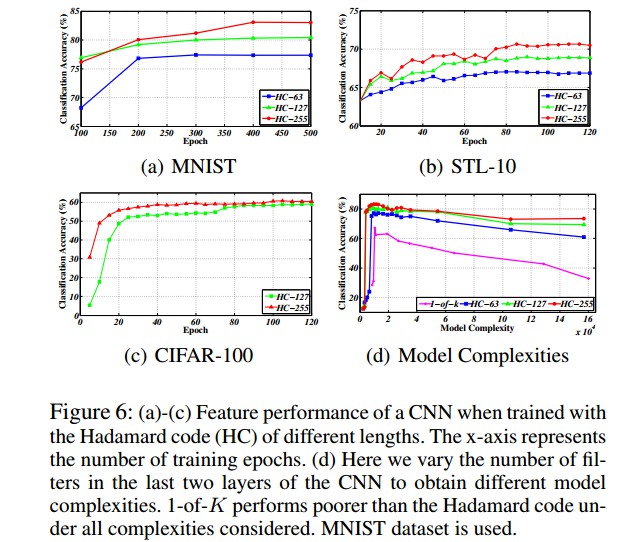
论文: Deep Representation Learning with Target Coding - AAAI2015
作者: Shuo Yang, Ping Luo, Chen Change Loy, Kenneth W. Shum, and Xiaoou Tang
团队: CUHK, CAS shenzhen
1-of-K code:长度为 K 的向量,第 k 个元素为 1,其它的为 0. [分类任务]
Target code:multi-label 预测问题.
图像分类一般采用单个类别标签作为 label,可以看做是 1-of-K 编码,类别标签所在位置的编码值为 1,其它非标签位置的编码值为 0.
Taget code 的方式,是将一个 class 类别表示为一个 0-1 向量,长度为 2 的乘方(幂)(如 2^3=8, 2^4=16, 2^5=32, 2^6=32, 作者代码给出的范围是 3-14),可能有多个位置的编码值为 1,而不仅仅是类别标签位置的编码值为 1. 假如数据集有 10 类(如 MNIST,Cifar10),则 class 类别的 label 向量长度至少为 2^4=16. 假如数据集有 1000 类(如 ImageNet),其Hadamard 矩阵至少为 2^10 × 2^10=1024,每 class 类别的label向量长度为 2^10=1024.
1. Target Coding 定义
假设 ${ \mathcal{T} }$ 为整数集,记为 字符集(alphabet set); ${ \mathcal{T} }$ 内的一个元素记为 符号(symbol). 如,${ \mathcal{T} = \lbrace 0, 1 \rbrace }$ 是一个二值字符集.
目标编码(target code) ${ \mathcal{S} }$ 是一个矩阵,${ \mathcal{S} \in \mathcal{T} ^{n×l} }$. 目标编码矩阵的每一行记为 码字(codeword). ${ l }$ 为每个码字(codeword)中的符号(symbols)数;n 为码字数(codewords).
对于目标编码 ${ \mathcal{S} }$,记 ${ \mathcal{A} = \lbrace \mathbf{\alpha}_{i}\rbrace_{i=1}^{n} }$ 为目标编码矩阵 ${ \mathcal{S} }$ 行元素的符号(symbols) 的经验分布集,如,当 i=1,2,...,n 时,${ \mathbf{\alpha}_i }$ 是长度为 ${ |\mathcal{T}| }$ 的向量,${ \mathbf{\alpha}_i }$ 的第 t 个元素是第 t 个符号(symbol) 在目标编码矩阵 ${ \mathcal{S} }$ 的第 i 行出现的频数.
同样地,记 ${ \mathcal{B} = \lbrace \mathbf{\beta}_{j}} \rbrace _{j=1}^{l}$ 为目标编码矩阵 ${ \mathcal{S} }$ 列元素的符号(symbols) 的经验分布集.
假设给定两个不同的行索引(row indices) ${ i }$ 和 ${ i^\prime }$,目标编码矩阵 ${ \mathcal{S} }$ 的 ${ i }$ 行和 ${ i^\prime }$ 行的 Hamming distance 为:${ |( j : \mathcal{S}_{ij} \ne \mathcal{S}_{i^\prime j} )| }$,即,Hamming 距离计算了两个向量中对应符号(symbol) 不相等的列索引数(column indices). 简便起见,将之记为 成对 Hamming 距离(pairwise Hamming distance).
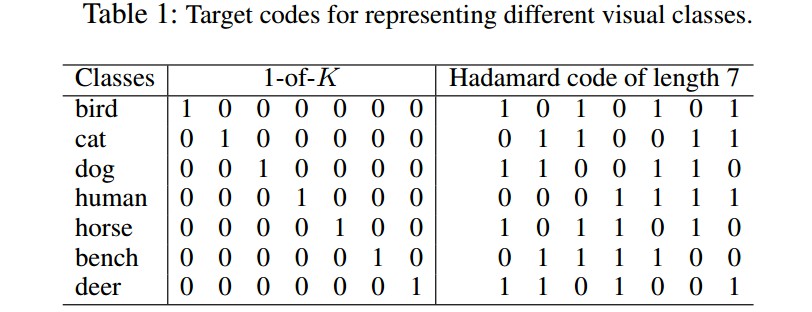
Table 1 中给除了一种一对多(1-of-K)的二值目标编码,深度学习中一般用于表示 K 类 classes. K 个符号(symbols) 中的每一个元素是 0 或 1,分别表示特定 class 的概率. 此时,可以看做是目标编码矩阵的一种特殊形式,即 ${ \mathcal{S} = I }$. ${ I \in \mathcal{T}^{K×K} }$ 的单位矩阵.
可以简单直接的的到 1-of-K 编码的某些属性. 如,
记 ${ \mathbf{\alpha}_{it} }$ 为矩阵 ${ \mathcal{S} }$ 第 i 行中第 t 个符号(symbol) 的数目,i = 1,2, ..., K,这里 t=1, symbol=0;t=2, symbol=1. 由于每个码字(codeword) 只有一个符号(symbol),能够得出 ${ \mathbf{\alpha}_{i1} = \frac{K-1}{K} }$,${ \mathcal{\alpha}_{i2} = \frac{1}{K} }$.
相似地,可以得到 ${ \mathbf{\beta}_{j1} = \frac{K-1}{K} }$,${ \mathbf{\beta}_{j2} = \frac{1}{K} }$. 成对 Hamming 距离为 2.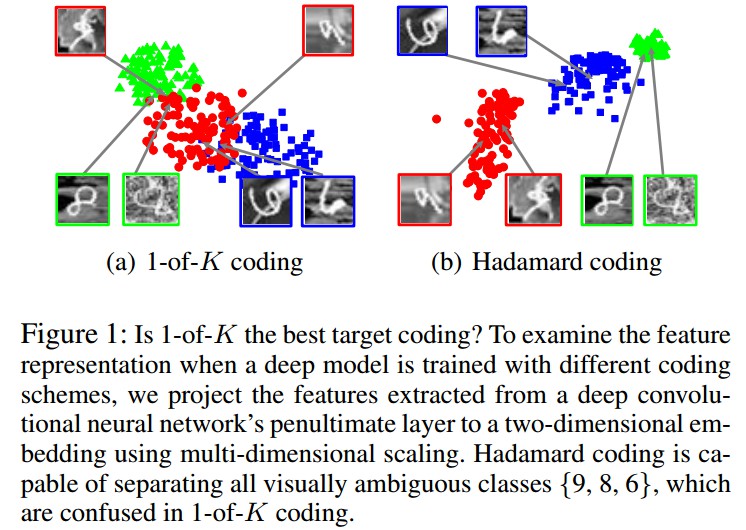
2. 基于 Hadamard Code 构建 Class label
目标编码(target coding) 不仅对于目标预测具有纠错(error-correcting)作用,还有助于学习更好的特征表示.
采用普遍使用的错误纠正编码(error-correcting code) 方法 —— Hadamard Code,其可以由 Hadamard 矩阵生成.
假设矩阵 ${ \mathcal{H} \in (+1,-1)^{m×m} }$,其元素是 +1 或 -1,如果 ${ \mathcal{H} \mathcal{H}^T = mI }$,则记该矩阵为 Hadamard 矩阵. 其中,${ I }$ 为单位矩阵. Hadamard 矩阵要求任意两个不同的行和列分别都是正交的.
Hadamard 矩阵采用 Sylvester(Hedayat and Wallis 1978) 方法生成. 如,
给定 Hadamard 矩阵 ${ \mathcal{H} ^2 = [+ +; + -] }$,采用 Kronecker 乘积,有:${ \mathcal{H}^4 = \mathcal{H}^2 \otimes \mathcal{H}^2 }$;类似地,${ \mathcal{H}^8 = \mathcal{H}^4 \otimes \mathcal{H}^2 }$. 可以看出,Hadamard 矩阵的尺寸是 2 的幂(乘方)关系.
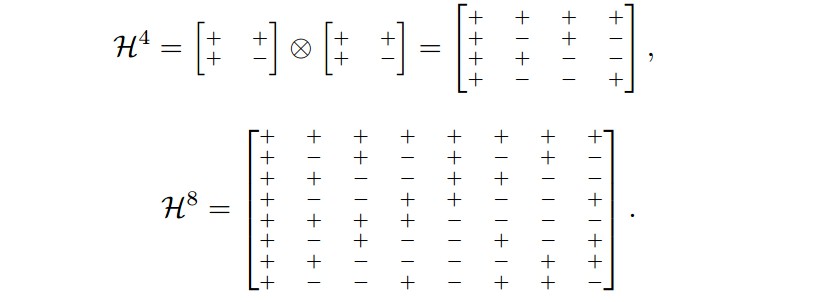
针对 Hadamard 矩阵的任意两个不同的行(或列),其长度为 m,则有 m/2 对元素的符号彼此相同,m/2 对元素的符号相反. 因此,任意两行的距离是常数,值等于 m/2.
现在,基于 Hadamard 矩阵,则可以构建目标编码矩阵 ${ \mathcal{S} }$.
假设 Hadamard 矩阵 ${ \mathcal{H} \in (+1,-1)^{m×m} }$,则去除 ${ \mathcal{H} }$ 的第一行和第一列,并将 +1 变成 0,-1 变成 1,即可的到目标编码矩阵 ${ \mathcal{S} \in \mathcal{T}^{(m-1) × (m-1)} }$. 根据 ${ \mathcal{H} }$ 的定义可知,矩阵 ${ \mathcal{S} }$ 的每一行和每一列都有 m/2 个 1. 由于 Hadamard 矩阵的任意两行都是正交的,则矩阵 ${ \mathcal{S} }$ 的成对 Hamming 距离等于 m/2.
Tabel 1 给出了一个由 ${ \mathcal{H}^8 }$ 得到的 7×7 目标编码矩阵 ${ \mathcal{S} }$.
实际上,由于 Hadamard 矩阵的长度 m 是 2 的幂(乘方),很难精确的到包含 K 个 classes 的 K 个码字(codewords). 故,记矩阵 ${ \mathcal{C} \in \mathcal{T} ^{K×(m-1)} }$ 是 K 个 classes labels 的矩阵,i = 1,2,...,K,第 i 个 class 是由矩阵 ${ \mathcal{C} }$ 的第 i 行标注的(labeled). 因此,矩阵 ${ \mathcal{C} }$ 是从目标编码矩阵 ${ \mathcal{S} \in \mathcal{T}^{(m-1)×(m-1)} }$ 中选取 K 个码字(codewords) 来构建的.
3. Target Coding 的属性
属性1. 目标编码矩阵 ${ \mathcal{S} }$ 每一行具有一致性.
Hadamard 编码的每一行都有 m/2 个符号(symbols) 等于 1.
矩阵行元素的一致性对于目标预测(target prediction) 会引入冗余(redundancy). 矩阵 ${ \mathcal{S} }$ 的每一行表示一个 class 类别标签.
与 1-of-K 编码不同的是,1-of-K 编码仅使用单个符号 ‘1’ 来表示 class 类别;
而 Hadamard 编码的每个码字(codeword) 都有相同数量的等于 ‘1’ 的冗余符号(symbols). 这种属性是错误纠正属性. 如果符号(symbols) 的有限数量的部分被损坏,仍更可能正确识别 object 类别.
符号 ‘1’ 的数量越多,则错误纠正能力越强,使得目标层(target layer)的响应能够直接用于最近邻分类.
属性2. 目标编码矩阵 ${ \mathcal{S} }$ 每一列具有一致性.
类似地,Hadamard 编码的每一列都有 m/2 个符号(symbols) 等于 1.
矩阵列元素的一致性也是特征表示学习需要的.
目标编码矩阵 ${ \mathcal{S} }$ 的每一列可以看做是一个决策函数(decision function),将输入空间分成两个平衡区域,如,近一般的 classes 类别在一个区域,剩下的 classes 类别被分组到另一个区域.
给定多个列,可以得到不同的划分区域,结合不同区域可能在输入空间产生指数个区域交叉(region intersections). 基于这样的属性,目标编码矩阵有助于产生更能区分数据的特征,的到数据的判别性和鲁棒性的特征描述.
属性3. 目标编码矩阵 $\mathcal{S}$ 的成对 Hamming 距离值为常数.
因为 Hadamard 编码的行和列都具有一致性,成对 Hamming 距离也是 $\frac{m}{2}$.
也就是说,任意两个码字(codewords) 间的 Hamming 距离都是码字(codewords) 长度的一半.
这种属性确保了,每一 class 类有其唯一的码字(codeword),并与其它 classes 类有相同的远离距离. 从同一 class 类采样的数据,被强制映射到相同的码字(codeword). 有助于特征不变性表示.
如前面说的,假设,Class 类别标签 ${ \mathcal{C} \in \mathcal{T}^{K×(m-1)} }$ 是通过从目标编码矩阵 ${ \mathcal{S} \in \mathcal{T}^{(m-1)×(m-1)} }$ 中选取 K 个码字(codewords) 构建的.
然而, 由于 $m$ 是 2 的乘方, 当 class 类别数小于 m-1 时,K < m-1,${ \mathcal{C} \in \mathcal{T}^{K×(m-1)} }$ 违背了属性2.
因此,提出一种贪婪搜索(greedy search)方法 来从矩阵 ${ \mathcal{S} }$ 中选取 ${ \mathcal{C} }$,以逼近 属性2.
从目标编码矩阵 ${ \mathcal{S} }$ 选取一个码字(codeword),当且仅当该码字(codeword)不破坏矩阵 ${ \mathcal{C} }$ 每一列的一致性时,才将该码字(codeword) 添加到矩阵 ${ \mathcal{C} }$.
例如,当 K=10, m=128 或 m=256 时,采用贪婪搜索和随机选取来构建矩阵 ${ \mathcal{C} }$. 如图: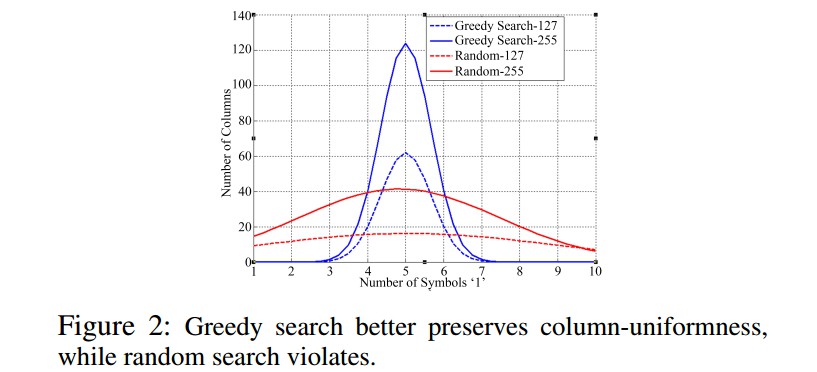
矩阵列中符号(symbol) ‘1’ 的数量分布情况如 Figure 2. 可以看出,贪婪搜索方法能够更好的体现矩阵列元素的一致性(理想情况,所有的列都包含 5 个符号(symbols) '1'. 采用贪婪搜索算法,当 m=256 时, 95% 的列都包含了 4-6 个符号(symbols) '1'). 随机选取会导致列元素一致性不够好.
4. CNN 中 Target Code 的应用
给定数据集 ${ \lbrace \mathbf{x}_i, \mathbf{y}_i \rbrace _{i=1}^{N} }$,
${ \mathbf{x}_i }$ 为第 i 个样本,
${ \mathbf{y}_i \in \mathcal{C} }$ 为对应的 class 类别标签,N 为样本总数.
采用CNN 来学习特征表示,损失函数采用 Euclidean loss:
${ \mathbf{W}_l }$ 和 ${ \mathbf{b}_l }$ 分别为第 ${ l }$ 层的权重和偏置.
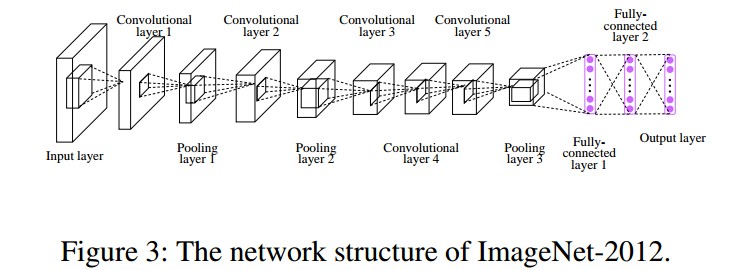
由于 Hadamard 编码与网络结构是独立的,因此,任何网络结构都可以. 例如图: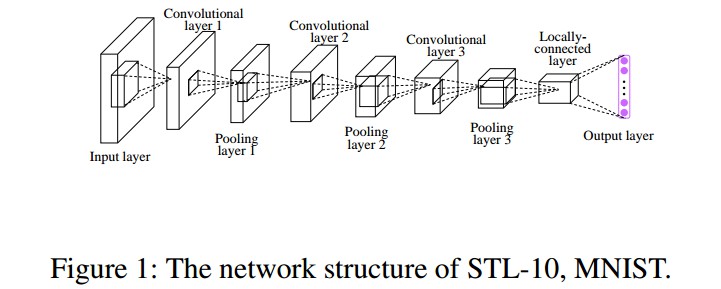
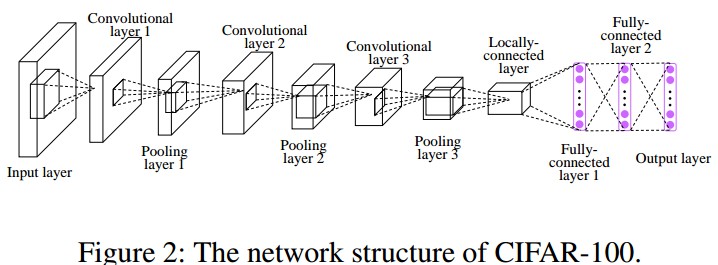
5. Results