原文:计算机视觉"新"范式: Transformer - 202010.16
出处:Smarter - 微信公众号
学习,记录.
自从Transformer出来以后,Transformer便开始在NLP领域一统江湖. 而Transformer在CV领域反响平平,一度认为不适合CV领域,直到最近计算机视觉领域出来几篇Transformer文章,性能直逼CNN的 SOTA,给予了计算机视觉领域新的想象空间.
本文不拘泥于 Transformer 原理和细节实现(知乎有很多优质的Transformer解析文章,感兴趣的可以看看),着重于Transformer对计算机视觉领域的革新.
首先简略回顾一下 Transformer,然后介绍最近几篇计算机视觉领域的Transformer文章,其中ViT用于图像分类,DETR 和 Deformable DETR 用于目标检测. 从这几篇可以看出,Transformer在计算机视觉领域的范式已经初具雏形,可以大致概括为:Embedding->Transformer->Head
一些有趣的点写在最后~~
1. Transformer
Transformer详解:
下面以机器翻译为例子,简略介绍Transformer结构.
1.1. Encoder-Decoder
Transformer结构可以表示为Encoder和Decoder两个部分:

Encoder 和 Decoder 主要由 Self-Attention 和 Feed-Forward Network 两个组件构成,Self-Attention 由 Scaled Dot-Product Attention 和 Multi-Head Attention 两个组件构成.
Scaled Dot-Product Attention公式:
$$ \text{Attention} (Q, K, V) = \text{softmax} (\frac{QK^T}{\sqrt{d_k}}) V $$
Multi-Head Attention公式:
$$ \text{MultiHead}(Q, K, V) = \text{Concat} (\text{head}_1, ..., \text{head}_{\text{h}} W^Q) $$
Feed-Forward Network公式:
$$ \text{FFN}(x) = \text{max}(0, xW_1 + b_1) W_2 + b_2 $$
1.2. Positional Encoding
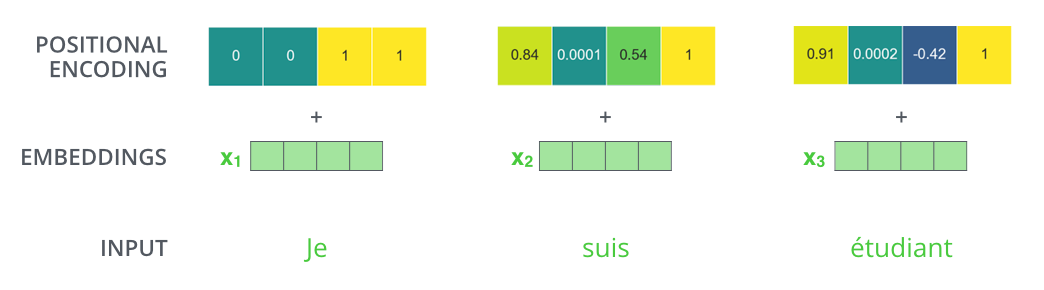
如图所示,由于机器翻译任务跟输入单词的顺序有关,Transformer 在编码输入单词的嵌入向量时引入了positional encoding,这样Transformer就能够区分出输入单词的位置了.
引入positional encoding的公式为:
$$ PE_{(pos, 2i)} = \text{sin} (\frac{pos}{10000^{\frac{2i}{d_{model}}}}) $$
$$ PE_{(pos, 2i+1)} = \text{cos} (\frac{pos}{10000^{\frac{2i}{d_{model}}}}) $$
其中,pos 是位置,i 是维数,dmodel 是输入单词的嵌入向量维度.
1.3. Self-Attention
1.3.1. Scaled Dot-Product Attention
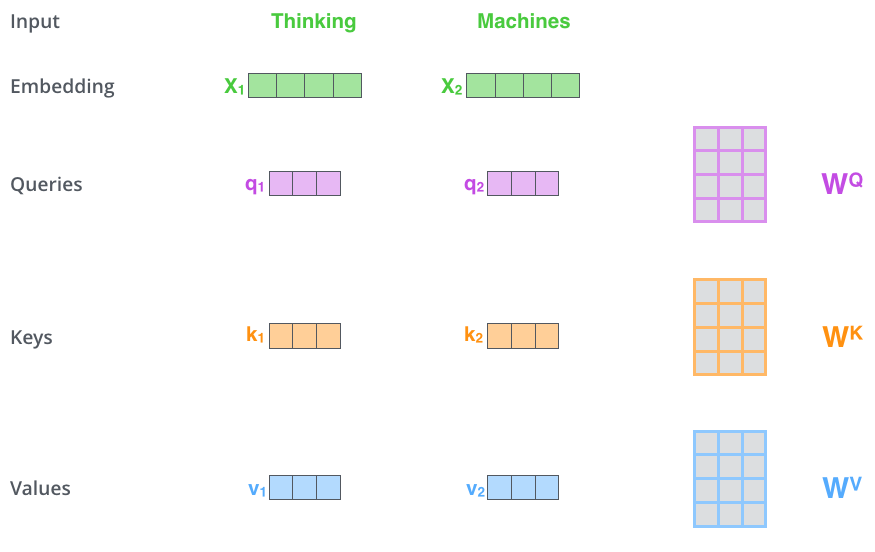
在 Scaled Dot-Product Attention中,每个输入单词的嵌入向量分别通过3个矩阵WQ、WK和 WV 来分别得到Query向量(Q),Key向量( K)和Value向量(V ).
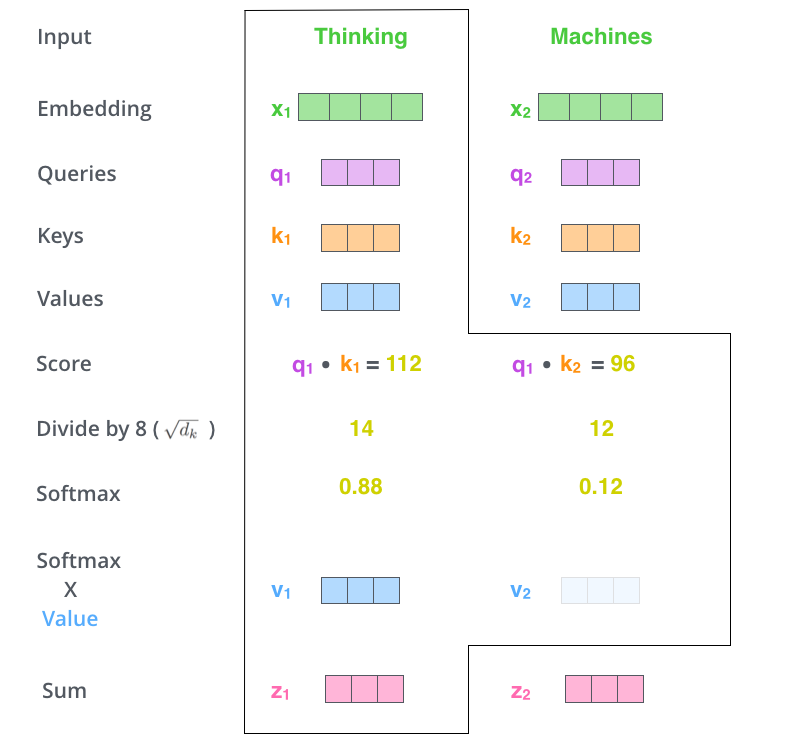
如图所示,Scaled Dot-Product Attention的计算过程可以分成7个步骤:
[1] - 每个输入单词转化为嵌入向量;
[2] - 根据嵌入向量得到 q, k, v 三个向量;
[3] - 通过 q, k 向量计算 score: $score = q \cdot k$;
[4] - 对 score 进行归一化,即除以 $\sqrt{d_k}$;
[5] - 通过 softmax 激活函数计算 score;
[6] - softmax 点乘 Value 值 v,得到每个输入向量的评分 v;
[7] - 所有输入向量的评分 v 之和为 z: $z \sum v$.
上述步骤的矩阵形式可以表示成:
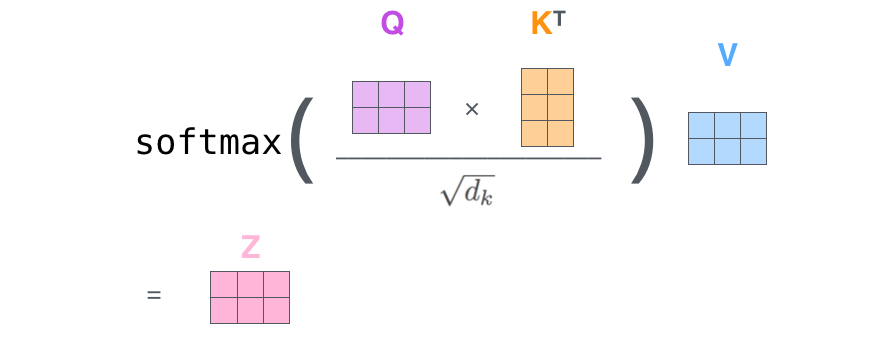
与Scaled Dot-Product Attention公式一致.
1.3.2. Multi-Head Attention

如图所示,Multi-Head Attention 相当于 h 个不同 Scaled Dot-Product Attention 的集成,以 h=8 为例子,Multi-Head Attention 步骤如下:
[1] - 将数据 $X$ 分别输入到 8 个不同的 Scaled Dot-Product Attention 中,得到8个加权后的特征矩阵 $Z_i, i \in \lbrace 1, 2, ..., 8 \rbrace$;
[2] - 将 8 个 $Z_i$ 按列拼成一个大的特征矩阵;
[3] - 特征矩阵经过一层全连接得到输出 $Z$.
Scaled Dot-Product Attention 和 Multi-Head Attention 都加入了 short-cut 机制.
2. Vision Transformer(ViT)
ViT 将 Transformer 巧妙的应用于图像分类任务,更少计算量下性能跟SOTA相当.

Vision Transformer(ViT) 将输入图片拆分成16x16个patches,每个 patch 做一次线性变换降维同时嵌入位置信息,然后送入 Transformer,避免了像素级 attention 的运算.
类似 BERT[class] 标记位的设置,ViT 在 Transformer 输入序列前增加了一个额外可学习的[class]标记位,并且该位置的 Transformer Encoder 输出作为图像特征.
$$ \pmb{z}_0 = [\pmb{x}_{\text{class}}; \pmb{x}_{\text{p}}^{1}\pmb{E}; \pmb{x}_{\text{p}}^{2}\pmb{E}; \cdots \pmb{x}_{\text{p}}^{N}\pmb{E} ] + \pmb{E}_{\text{pos}} $$
其中,
$\pmb{E} \in R ^{P^2 \cdot C} \times D$;
$\pmb{E} \in R ^{(N+1) \times D}$.
$$ \pmb{z} _l^{'} = \text{MSA} (\text{LN}(\pmb{z}_{l-1})) + \pmb{z}_{l -1} $$
$$ \pmb{z} _l = \text{MLP} (\text{LN}(\pmb{z} _l^{'})) + \pmb{z} _l^{'} $$
$$ \pmb{y} = \text{LN}(\pmb{z} _l^{0}) $$
其中,$l = 1 ... L$.
$(H, W)$ 为原图像分辨率,$(P, P)$ 为每个图像 patch 的分辨率,$N = \frac{HW}{P^2}$ 为 Transformer 输入序列的长度.
ViT 舍弃了CNN的归纳偏好问题,更加有利于在超大规模数据上学习知识,即大规模训练优归纳偏好,在众多图像分类任务上直逼SOTA.
3. DETR
DETR 使用 set loss function 作为监督信号来进行端到端训练,然后同时预测所有目标,其中 set loss function 使用 bipartite matching 算法将 pred 目标和 gt 目标匹配起来. 直接将目标检测任务看成set prediction 问题,使训练过程变的简洁,并且避免了anchor、NMS等复杂处理.
DETR主要有两个部分:architecture 和 set prediction loss.
3.1. Architecture

[1] - DETR 先用 CNN 将输入图像 embedding 成一个二维表征;
[2] - 然后将二维表征转换成一维表征并结合 positional encoding 一起送入 encode;
[3] - decoder 将少量固定数量的已学习的 object queries(可以理解为 positional embeddings)和 encoder 的输出作为输入.
[4] - 最后将 decoder 得到的每个 output embdding 传递到一个共享的前馈网络(FFN),该网络可以预测一个检测结果(包括类和边框)或着“没有目标”的类.
3.1.1. Transformer
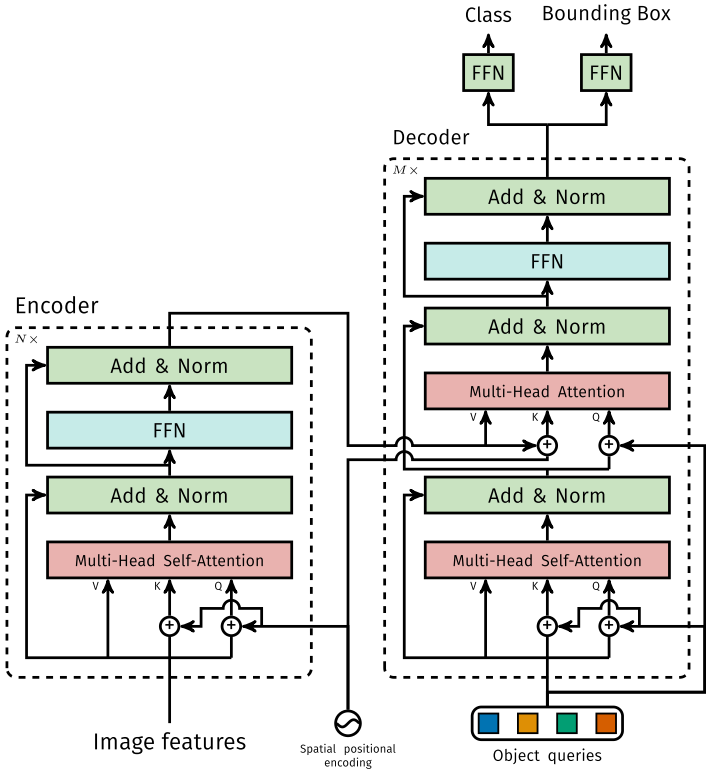
[1] - Encoder
将 Backbone 输出的 feature map 转换成一维表征,得到 $d \times HW$ 特征图,然后结合 positional encoding 作为 Encoder 的输入. 每个 Encoder 都由 Multi-Head Self-Attention 和 FFN 组成.
和 Transformer Encoder 不同的是,因为 Encoder 具有位置不变性,DETR 将 positional encoding 添加到每一个 Multi-Head Self-Attention 中,来保证目标检测的位置敏感性.
[2] - Decoder
因为 Decoder 也具有位置不变性,Decoder 的 $N$ 个object query (可以理解为学习不同object的positional embedding)必须是不同,以便产生不同的结果,并且同时把它们添加到每一个 Multi-Head Attention 中. $N$ 个 object queries 通过 Decoder 转换成一个 output embedding,然后output embedding 通过 FFN 独立解码出 $N$ 个预测结果,包含 box 和 class. 对输入 embedding 同时使用 Self-Attention 和 Encoder-Decoder Attention,模型可以利用目标的相互关系来进行全局推理.
和 Transformer Decoder 不同的是,DETR 的每个 Decoder 并行输出 个对象,Transformer Decoder 使用的是自回归模型,串行输出 个对象,每次只能预测一个输出序列的一个元素.
[3] - FFN
FFN 由 3 层 perceptron 和一层 linear projection 组成. FFN 预测出 box 的归一化中心坐标、长、宽和class.
DETR 预测的是固定数量的 $N$ 个box的集合,并且 $N$ 通常比实际目标数要大的多,所以使用一个额外的空类来表示预测得到的box不存在目标.
3.2. Set prediction loss
DETR 模型训练的主要困难是如何根据 gt 衡量预测结果(类别、位置、数量).
DETR 提出的 loss 函数可以产生 pred 和 gt 的最优双边匹配(确定pred和gt的一对一关系),然后优化loss.
将 $y$ 表示 gt 的集合,表示为 $N$ 个预测结果的集合. 假设 $N$ 大于图片目标数,$y$ 可以认为是用空目标类(无目标) 填充的大小为 $N$ 的集合. 搜索两个集合 $N$ 个元素 $\sigma \in \wp _N$ 的不同排列顺序,使得 loss 尽可能的小的排列顺序即为二分图最大匹配(Bipartite Matching),公式如下:
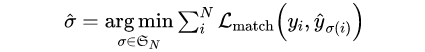
其中,$\mathcal{L}_{\text{match}} (y_i, \hat{y}_{\sigma(i)})$ 表示 pred 和 gt 关于 $\sigma(i)$ 元素 $i$ 的匹配 loss. 其中二分图匹配通过匈牙利算法(Hungarian algorithm)得到.
匹配 loss 同时考虑了 pred class 和 pred box 的准确性. 每个 gt 的元素 $i$ 可以看成 $y_i = (c_i, b_i)$,其中,$c_i$ 表示 class label (可能是空类), $b_i$ 表示 gt box,将元素 $i$ 二分图匹配指定的 pred class 表示为 $\hat{p}_{\sigma(i)}(c_i)$,pred box 表示为 $\hat{b}_{\sigma(i)}$.
第一步先找到一对一匹配的 pred 和 gt,第二步再计算 hungarian loss.
hungarian loss公式如下:
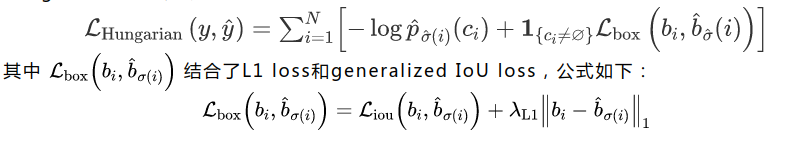
ViT和DETR两篇文章的实验和可视化分析很有启发性,感兴趣的可以仔细看看~~
4. Deformable DETR
从 DETR 看,还不足以赶上 CNN,因为训练时间太久了,Deformable DETR的出现,让作者对Transformer有了新的期待.
Deformable DETR 将 DETR 中的 attention 替换成 Deformable Attention,使DETR范式的检测器更加高效,收敛速度加快10倍.

Deformable DETR 提出的 Deformable Attention 可以缓解 DETR 的收敛速度慢和复杂度高的问题. 同时结合了 deformable convolution 的稀疏空间采样能力和transformer的关系建模能力.
Deformable Attention 可以考虑小的采样位置集作为一个pre-filter突出所有feature map的关键特征,并且可以自然地扩展到融合多尺度特征,并且Multi-scale Deformable Attention本身就可以在多尺度特征图之间进行交换信息,不需要FPN操作.
4.1. Deformable Attention Module
给定一个query元素(如输出句子中的目标词)和一组key元素(如输入句子的源词),Multi-Head Attention 能够根据 query-key pairs 的相关性自适应的聚合key的信息. 为了让模型关注来自不同表示子空间和不同位置的信息,对multi-head的信息进行加权聚合.
其中 $q \in \Omega _q$ 表示query元素(特征表示为 $\mathcal{z}_q \in R^{C}$),$q \in \Omega_k$ 表示 key 元素(特征表示为 $\mathcal{z}_k \in R^{C}$),$C$ 是特征维度,$\Omega_q$ 和 $\Omega_k$ 分别为 $q$ 和 $k$ 的集合.
那么Transformer 的 Multi-Head Attention公式表示为:
$$ \text{MultiHeadAttn}(\mathcal{z}_1, x) = \sum_{m=1}^{M} W_m [\sum_{k \in \Omega_k} A_{mqk} \cdot W_{m}^{'} x_k] $$
其中,$m$ 指定 attention head, $W_m^{'} \in R^{c_v \times C}$ 和 $W_{m} \in R ^{C_v \times C}$ 是可学习参数.
注意力权重 $A_{mqk} \propto \text{exp} \lbrace \frac{z_q^T U_m^T V_m x_k}{\sqrt{C_v}} \rbrace$ 并且归一化 $\sum A_{mqk} = 1$. 其中,$U_m, V_m \in R ^{C_{v} \times C}$是可学习参数. 为了能够分辨不同空间位置,$z_q$ 和 $x_k$ 通常会引入positional embedding.
对于 DETR 中的 Transformer Encoder,query 和 key 元素都是 feature map 中的像素.
DETR 的 Multi-Head Attention 公式表示为:
$$ \text{Attn}(\mathcal{z}_q, x) = \sum_{m=1}^M W_m [\sum_{k=1}^K A_{mqk} \cdot W_{m}^{'} x] $$
其中,$K = H \times W$.
DETR 主要有两个问题:需要更多的训练时间来收敛,对小目标的检测性能相对较差. 本质上是因为 Transfomer 的 Multi-Head Attention 会对输入图片的所有空间位置进行计算.
而 Deformable DETR 的 Deformable Attention 只关注参考点周围的一小部分关键采样点,为每个 query 分配少量固定数量的 key,可以缓解收敛性和输入分辨率受限制的问题.
给定一个输入feature map ,$q$ 表示为query元素(特征表示为),二维参考点表示为$p_q$,Deformable DETR 的 Deformable Attention公式表示为:
$$ \text{DeformAttn}(\mathcal{z}_q, p_q, x) = \sum_{m=1}^{M} W_m [\sum_{k=1}^{K} A_{mqk} \cdot W_{m}^{'} x (p_q + \Delta p_{mqk})] $$
其中,$m$ 指定 attention head, $k$ 指定采样的 key,$K$ 表示采样 key 的总和($K << HW$).
$\Delta p_{mqk}, A_{mqk}$ 分别表示第 $k$ 个采样点在第 $m$ 个 attention head 的采样偏移量和注意力权重. 注意力权重 $A_{mqk}$ 在 [0, 1] 范围内,且归一化 $\sum_{k=1}^K A_{mqk} = 1$.
$\Delta p_{mqk} \in R ^2$ 表示为无约束范围的二维实数.
因为 $p_q + \Delta p_{mqk}$ 为分数,需要采用双线性插值方法计算 $x(p_q + \Delta p_{mqk})$.
4.2.2. Multi-scale Deformable Attention Module
Deformable Attention可以很自然地扩展到多尺度的feature maps.
$\lbrace x^l \rbrace$ 表示为输入的多尺度feature maps,$x^l \in R ^{C \times H_l \times W_l}$.
$\hat{p}_q \in [0, 1]^2$ 表示为每个query元素 $q$ 的参考点 $p$ 的归一化坐标.
Deformable DETR 的 Multi-scale Deformable Attention公式表示为:
$$ \text{MSDeformAttn}(z_q, \hat{p}_q, \lbrace x^l \rbrace _{l=1}^L) = \sum_{m=1}^M W_m [\sum_{l=1}^L \sum_{k=1}^K A_{mlqk} \cdot W_m^{'} x^l (\phi_l(\hat{p}_q) + \Delta p_{mlqk})] $$
其中,$m$ 指定 attention head. $l$ 指定输入特征层,$k$ 指定采样的 key,$K$ 表示采样 key 的总数 ($K << HW$).
$\Delta p_{mlqk}, A_{mlqk}$ 分别表示第 $k$ 个采样点在第 $l$ 特征层的第 $m$ 个 attention head 的采样偏移量和注意力权重. 注意力权重 $A_{mlqk}$ 在 [0, 1] 范围内,且归一化 $\sum_{k=1}^K A_{mlqk} = 1$.
4.2.3. Deformable Transformer Encoder
将DETR中所有的 attention 替换成multi-scale deformable attention.
Encoder 的输入和输出都是具有相同分辨率的多尺度feature maps.
Encoder 从 ResNet 的 C3-C6 中抽取多尺度 feature maps $\lbrace x^l \rbrace _{l=1}^L (L=4)$,(C6 由 C5 进行 3x3 stride 2 卷积得到).
在 Encoder 中使用 multi-scale deformable attention,输出是和输入具有相同分辨率的多尺度feature maps. query 和 key 都来自多尺度 feature maps 的像素. 对于每个query像素,参考点是它本身. 为了判断 query 像素源自哪个特征层,除了 positional embedding 外,还添加了一个scale-level embedding $\lbrace e^l \rbrace _{l=1}^L$,不同于 positional embedding 的固定编码, scale-level embedding 随机初始化并且通过训练得到.
4.2.4. Deformable Transformer Decoder
Decoder 中有 cross-attention 和 self-attention 两种注意力. 这两种注意力的 query 元素都是 object queries.
在 cross-attention 中,object queries 从 feature maps 中提取特征,而 key 元素是 encoder输出的feature maps.
在 self-attention 中,object queries之间相互作用,key 元素也是object queries.
因为 Deformable Attention 是用于 key 元素的 feature maps 特征提取的,所以 decoder 部分,deformable attention 只替换 cross-attention.
因为 multi-scale deformable attention 提取参考点周围的图像特征,让检测头预测 box 相对参考点的偏移量,进一步降低了优化难度.
5. 复杂度分析
假设 query 和 key 的数量分别为 $n_q$ 和 $n_k$,其中($n_q = n_k$),维度为 $d$,key 采样点数为 $k$,图像的 feature map 大小为 $d \times H \times W$,卷积核尺寸为 $k$.
5.1. Convolution 复杂度
[1] - 为了保证输入和输出在第一个维度都相同,故需要对输入进行padding操作,因为这里 kernel size 为 $k$ (实际 kernel 的形状为 $k \times k \times d$).
[2] - 大小为 $k \times k$ 的卷积核一次运算复杂度为 $O(k^2 d)$,一共做了 $H \times W$ 次,姑复杂度为 $O(HW k^2 d)$.
[3] - 为了确保第三个维度相等,故需要 $d$ 个卷积核,所以卷积操作的时间复杂度为 $O(HWK^2 d^2)$.
5.2. Self-Attention 复杂度
$$ \text{Attention} (Q, K, V) = \text{softmax} (\frac{QK^T}{\sqrt{d_k}}) V $$
[1] - $Q, K, V$ 的计算复杂度为 $n \times d$.
[2] - 相似度计算 $QK^T$: $n \times d$ 与 $d \times n$ 运算,得到 $n \times n $ 矩阵,复杂度为 $O(n^2 d)$.
[3] - softmax 计算:对每行做 softmax,复杂度为 $O(n)$,则 $n$ 行的复杂度为 $O(n^2)$.
[4] - 加权和:$n \times n$ 与 $n \times d$ 运算,得到 $n \times d$ 矩阵,复杂度为 $O(n^2 d)$.
[5] - 最后,Self-Attention 的时间复杂度为 $O(n^2 d)$.
5.3. Transformer 复杂度
Self-Attention 的时间复杂度为 $O(n^2 d)$.
5.4. ViT
$N = H \times W / P^2$.
Self-Attention 的复杂度为 $O(H^2 W^2 d/P^4)$.
5.5. DETR
$n = H \times W$
Self-Attention 的复杂度为 $O(H^2 W^2 d)$.
5.6. Deformable DETR
Self-Attention的复杂度为 $O(HWd^2)$.
分析细节看原论文.
6. 几个问题
6.1. Q,K,V 如何理解?为什么不使用相同的 Q 和 K?
[1] - 从点乘的物理意义上讲,两个向量的点乘表示两个向量的相似度.
[2] - $Q, K, V$ 的物理意义是一样的,都表示同一个句子中不同 token 组成的矩阵. 矩阵的每一行,是表示一个 token 的 word embedding 向量. 假设一个句子“Hello, how are you?” 长度是6,embedding 维度是300,那么 $Q, K, V$ 都是 (6, 300) 的矩阵.
所以,$K$ 和 $Q$ 的点乘可以理解为计算一个句子中每个 token 相对于句子中其他 token 的相似度,这个相似度可以理解为 attetnion score,关注度得分. 虽然有了 attention score 矩阵,但是这个矩阵是经过各种计算后得到的,已经很难表示原来的句子了,而 $V$ 还代表着原来的句子,所以可以将attention score 矩阵与 $V$ 相乘,得到的是一个加权后的结果.
经过上面的解释,我们知道 $K$ 和 $Q$ 的点乘是为了得到一个 attention score 矩阵,用来对 $V$ 进行提炼. $K$ 和 $Q$ 使用不同的 $W_K$ 和 $W_Q$ 来计算,可以理解为是在不同空间上的投影. 正因为有了这种不同空间的投影,增加了表达能力,这样计算得到的 attention score 矩阵的泛化能力更高.
这里解释下该文作者理解的泛化能力,因为 $K$ 和 $Q$ 使用不同的 $W_K$ 和 $W_Q$ 来计算,得到的也是两个完全不同的矩阵,所以表达能力更强. 但如果不用 $Q$,直接拿 $K$ 和 $K$ 点乘的话,attention score 矩阵是一个对称矩阵,所以泛化能力很差,这个矩阵对 $V$ 进行提炼,效果会变差.
详细分析可以看链接文章
https://medium.com/dissecting-bert/dissecting-bert-part-1-d3c3d495cdb3
6.2. 如何Position Embedding更好?
目前还是一个开放问题,知乎上有一些优质的讨论,详细分析可以看链接文章
NLP: https://www.zhihu.com/question/347678607/answer/864217252
CV: https://zhuanlan.zhihu.com/p/99766566
6.3. ViT为什么要增加一个[CLS]标志位? 为什么将[CLS]标志位对应的向量作为整个序列的语义表示?
和 BERT 相类似,ViT 在序列前添加一个可学习的 [CLS] 标志位.
以BERT为例,BERT 在第一句前添加一个[CLS]标志位,最后一层该标志位对应的向量可以作为整句话的语义表示,从而用于下游的分类任务等.
将[CLS]标志位对应的向量作为整个文本的语义表示,是因为与文本中已有的其它词相比,这个无明显语义信息的符号会更“公平”地融合文本中各个词的语义信息,从而更好的表示整句话的语义.
6.4. 归纳偏好是什么?
归纳偏置在机器学习中是一种很微妙的概念:在机器学习中,很多学习算法经常会对学习的问题做一些假设,这些假设就称为归纳偏好(Inductive Bias).
归纳偏置可以理解为,从现实生活中观察到的现象中归纳出一定的规则(heuristics),然后对模型做一定的约束,从而可以起到“模型选择”的作用,即从假设空间中选择出更符合现实规则的模型. 可以把归纳偏好理解为贝叶斯学习中的“先验”.
在深度学习中,也使用了归纳偏好. 在CNN中,假设特征具有局部性(Locality)的特点,即把相邻的一些特征融合到一起,会更容易得到“解”;在RNN中,假设每一时刻的计算依赖于历史计算结果;还有attention机制,也是从人的直觉、生活经验归纳得到的规则.
而Transformer可以避免CNN的局部性归纳偏好问题. 举一个DETR中的例子.

训练集中没有超过13只长颈鹿的图像,DETR实验中创建了一个合成的图像来验证DETR的泛化能力,DERT可以完全找到合成的全部24只长颈鹿. 这证实了DETR避免了CNN的归纳偏好问题.
6.5. 二分图匹配? 匈牙利算法?
给定一个二分图 G,在 G 的一个子图M中,M的边集{E}中的任意两条边都不依附于同一个顶点,则称M是一个匹配. 求二分图最大匹配可以用匈牙利算法.
详细分析可以看链接文章
https://liam.page/2016/04/03/Hungarian-algorithm-in-the-maximum-matching-problem-of-bigraph/
6.6. BETR 的positional embedding、object queries和slot三者之间有何关系?

DETR可视化 decoder 预测得到的 20 个slot. 可以观察到每个slot学习到了特定区域的尺度大小. Object queries 从这个角度看,其实有点像 Faster-RCNN 等目标检测器的anchor,结合 encoder 的positional embedding 信息让每个 slot 往学习到的特定区域去寻找目标.
6.7. Transformer相比于CNN的优缺点?
优点:
Transformer关注全局信息,能建模更加长距离的依赖关系,而CNN关注局部信息,全局信息的捕捉能力弱.
Transformer避免了CNN中存在的归纳偏好问题.
缺点:
Transformer复杂度比CNN高,但是ViT和Deformable DETR给出了一些解决方法来降低Transformer的复杂度.
7. 总结
Transformer给图像分类和目标检测方向带来了巨大革新,分割、跟踪、视频等方向也不远了吧
NLP和CV的关系变的越来越有趣了,虽然争议很大,但是试想一下,NLP和CV两个领域能用一种范式来表达,该有多可怕,未来图像和文字是不是可以随心所欲的转来转去?可感知可推理的强人工智能是不是不远了?(想想就好)
向着NLP和CV的统一前进
Reference
[1] - Attention Is All You Need
[2] - An Image is Worth 16*16 Words: Transformers for Image Recognition at Scale
[3] - End-to-End Object Detection with Transformers
[4] - Deformable DETR: Deformable Transformers for End-to-End Object Detection