原文：一文打尽目标检测NMS——精度提升篇 - 2020.07.01 - 知乎

作者：曲終人不散丶

众所周知，非极大值抑制NMS是目标检测常用的后处理算法，用于剔除冗余检测框，本文将对可以提升精度的各种NMS方法及其变体进行阶段性总结.

总体概要：

对NMS进行分类，大致可分为以下六种，这里是依据它们在各自论文中的核心论点进行分类，这些算法可以同时属于多种类别.

  1. 分类优先：传统NMS，Soft-NMS (ICCV 2017)
  2. 定位优先：IoU-Guided NMS (ECCV 2018)
  3. 加权平均：Weighted NMS (ICME Workshop 2017)
  4. 方差加权平均：Softer-NMS (CVPR 2019)
  5. 自适应阈值：Adaptive NMS (CVPR 2019)
  6. +中心点距离：DIoU-NMS (AAAI 2020)

1. 分类优先

1.1. 传统 NMS

传统NMS有多个名称，据不完全统计可以被称为：Traditional/Original/Standard/Greedy NMS，为统一起见，下称Traditional NMS.

Traditional NMS算法是最为经典的版本，伪代码如下：

作为最为人所知晓的版本，Traditional NMS不仅有CPU版本，并且现已有GPU版本，GPU版本为Ross Girshick大神编写，俗称CUDA NMS. 多个深度学习框架也已将CUDA NMS纳入，作为基本函数使用，如Pytorch在Torchvision 0.3中正式集成了CUDA NMS.

缺点：

  1. 顺序处理的模式，计算IoU拖累了运算效率.
  2. 剔除机制太严格，依据NMS阈值暴力剔除.
  3. 阈值是经验选取的.
  4. 评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面.

1.2. Soft-NMS

Soft-NMS是Traditional NMS的推广，主要旨在缓解Traditional NMS的第二条缺点.

数学上看，Traditional NMS的剔除机制可视为：

$$ s_i = \begin{cases} 0 & IoU(M, B_i) \geq thresh \\ s_i & IoU(M, B_i) <thresh \end{cases} $$

显然，对于 IoU≥NMS阈值的相邻框，Traditional NMS的做法是将其得分暴力置0. 这对于有遮挡的案例较不友好. 因此Soft-NMS的做法是采取得分惩罚机制，使用一个与IoU正相关的惩罚函数对得分 $s$ 进行惩罚.

线性惩罚：

$$ s_i = \begin{cases} s_i(1 - IoU(M, B_i)) & DIoU(M, B_i) \geq thresh \\ s_i & DIoU(M, B_i) <thresh \end{cases} $$

其中，$M$ 代表当前的最大得分框.

线性惩罚有不光滑的地方，因而还有一种高斯惩罚：

$$ s_i = s_i e ^{- \frac{IoU(M, B_i)^2}{\sigma}} $$

在迭代终止之后，Soft-NMS依据预先设定的得分阈值来保留幸存的检测框，通常设为0.0001.

该文对两种惩罚方法的超参数也进行了实验，结果验证了超参数的不敏感性. 经作者实测，Soft-NMS在Faster R-CNN中的提升约有0.5-0.8个点的AP提升.

缺点：

  1. 仍然是顺序处理的模式，运算效率比Traditional NMS更低.
  2. 对双阶段算法友好，而在一些单阶段算法上可能失效.
  3. 如果存在定位与得分不一致的情况，则可能导致定位好而得分低的框比定位差得分高的框惩罚更多(遮挡情况下).
  4. 评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面.

2. 定位优先

IoU-Guided NMS出现于 IoU-Net 一文中，研究者认为框的定位与分类得分可能出现不一致的情况，特别是框的边界有模棱两可的情形时. 因而该文提出了IoU预测分支，来学习定位置信度，进而使用定位置信度来引导NMS.

具体来说，就是使用定位置信度作为NMS的筛选依据，每次迭代挑选出最大定位置信度的框M，然后将IoU≥NMS阈值的相邻框剔除，但把冗余框及其自身的最大分类得分直接赋予M，这样一来，最终输出的框必定是同时具有最大分类得分与最大定位置信度的框.

优点：

IoU-Guided NMS有助于提高严格指标下的精度，如AP75, AP90.

缺点：

  1. 顺序处理的模式，运算效率与Traditional NMS相同.
  2. 需要额外添加IoU预测分支，造成计算开销.
  3. 评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面.

3. 加权平均

多框共同决定一框

Weighted NMS出现于ICME Workshop 2017 Inception Single Shot MultiBox Detector for object detection 一文中. 论文认为Traditional NMS每次迭代所选出的最大得分框未必是精确定位的，冗余框也有可能是定位良好的. 那么与直接剔除机制不同，Weighted NMS顾名思义是对坐标加权平均，加权平均的对象包括M 自身以及IoU≥NMS阈值的相邻框.

$$ M = \frac{\sum_i w_i B_i}{\sum_i w_i} $$

$$ B_i \in \lbrace B|IoU(M, B) \geq thresh \rbrace \cup \lbrace M \rbrace $$

加权的权重为 $w_i = s_i IoU(M, B_i)$，表示得分与 Iou 的乘积.

优点：

Weighted NMS通常能够获得更高的Precision和Recall，以作者的使用情况来看，只要NMS阈值选取得当，Weighted NMS 均能稳定提高AP与AR，无论是AP50还是AP75，也不论所使用的检测模型是什么.

缺点：

  1. 顺序处理模式，且运算效率比Traditional NMS更低.
  2. 加权因子是IoU与得分，前者只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面；而后者受到定位与得分不一致问题的限制.

4. 方差加权平均

Softer-NMS同样是坐标加权平均的思想，不同在于权重 $w_i$ 发生变化，以及引入了box边界的不确定度.

关于目标检测box不确定度，可参考笔者的另一篇文章《一文了解目标检测边界框概率分布》

加权公式如下：

在加权平均的过程中，权重越大有两种情形：1. 与 M 的IoU越大；2. 方差越小，代表定位不确定度越低.

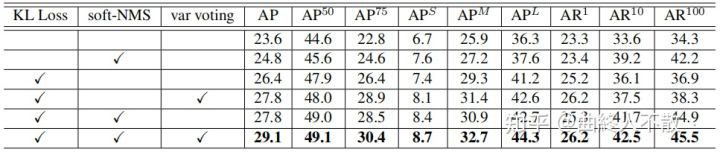
var voting表示方差加权平均

优点：

  1. 可以与Traditional NMS或Soft-NMS结合使用.
  2. 通常可以稳定提升AP与AR.

缺点：

  1. 顺序处理模式，且运算效率比Traditional NMS更低.
  2. 需要修改模型来预测方差.
  3. 加权因子是IoU与方差，前者依然只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面.

5. 自适应阈值

以上这些NMS都基于这样的假设：与当前最高得分框重叠越大，越有可能是冗余框.

Adaptive NMS的研究者认为这在物体之间有严重遮挡时可能带来不好的结果. 我们期望当物体分布稀疏时，NMS大可选用小阈值以剔除更多冗余框；而在物体分布密集时，NMS选用大阈值，以获得更高的召回. 既然如此，该文提出了密度预测模块，来学习一个框的密度.

一个 GT 框 $B_i$ 的密度标签定义如下：

$$ d_i = max_{B_i, Bj \in GT} IoU (B_i, B_j), i \neq j $$

模型的输出将变为 (x, y, w, h, s, d)，分别代表box坐标，宽高，分类得分，密度，其中密度 d 越大，代表该框所处的位置的物体分布越密集，越有可能是遮挡严重的地方；反之密度 d 越小，代表该框所处的位置的物体分布越稀疏，不太可能有遮挡.

论文以Traditionnal NMS和Soft-NMS的线性惩罚为基础，将每次迭代的NMS阈值更改如下：

$$ N_t = max \lbrace thresh, d_M \rbrace $$

其中，$thresh$ 代表最小的 NMS 阈值.

优点：

  1. 可以与前面所述的各种NMS结合使用.
  2. 对遮挡案例更加友好.

缺点：

  1. 与Soft-NMS结合使用，效果可能倒退 (受低分检测框的影响).
  2. 顺序处理模式，运算效率低.
  3. 需要额外添加密度预测模块，造成计算开销.
  4. 评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面.

6. +中心距离

DIoU-NMS出现于Distance-IoU一文，研究者认为若相邻框的中心点越靠近当前最大得分框 M 的中心点，则其更有可能是冗余框. 也就是说，考虑IoU相同的情况，如下所示

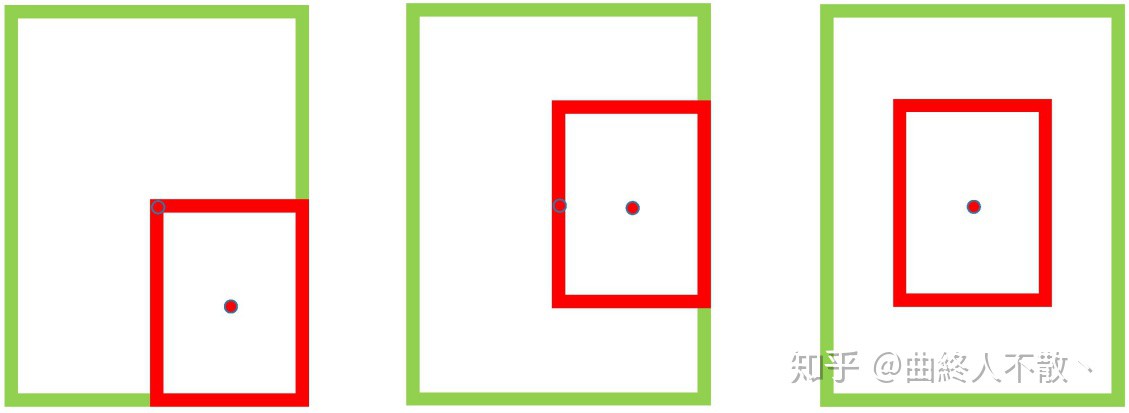
第一种相比于第三种越不太可能是冗余框. 基于该观点，研究者使用所提出的DIoU替代IoU作为NMS的评判准则，公式如下：

$$ s_i = \begin{cases} 0 & DIoU(M, B_i) \geq thresh \\ s_i & DIoU(M, B_i) <thresh \end{cases} $$

DIoU 的定义为：

$$ DIoU = IoU - \frac{d^2}{c^2} $$

而在实际操作中，研究者还引入了参数 $\beta$，用于控制 $\frac{d^2}{c^2}$ 的惩罚程度, 即：

$$ DIoU = IoU - (\frac{d^2}{c^2})^{\beta} $$

由公式可以看出，

  1. 当 $\beta \rightarrow \propto$ 时，DIou 退化为 IoU，此时，DIoU-NMS 与Traditional NMS效果相当.
  2. 当 $\beta \rightarrow 0$ 时，此时，几乎所有中心店不与 M 重合的框被保留了.

研究者进一步比较了Traditional NMS和DIoU-NMS的性能，在YOLOv3和SSD上，选取NMS阈值为[0.43,0.48]. 可以看到DIoU-NMS在每个阈值上都优于Traditional NMS，此外还值得一提的是，即便是性能最差的DIoU-NMS也比性能最好的Traditional NMS相当或更优，说明即便不仔细调整NMS阈值，DIoU-NMS也通常能够表现更好.

YOLOv3(左)和SSD(右)在VOC 2007 test集

这里顺便一提，既然都比了[0.43, 0.48]的阈值，就让人比较好奇更宽的阈值范围会怎样？Traditional NMS会不会有反超DIoU-NMS的情况？当然我个人比较认同DIoU-NMS更优的范围会大一些，也就是NMS阈值不必精调也可放心使用DIoU-NMS.

优点：

  1. 从几何直观的角度，将中心点考虑进来有助于缓解遮挡案例.
  2. 可以与前述NMS变体结合使用.
  3. 保持NMS阈值不变的情况下，必然能够获得更高recall (因为保留的框增多了)，至于precision就需要调 ![[公式]](https://www.zhihu.com/equation?tex=%5Cbeta) 来平衡了.
  4. 个人认为+中心点距离的后处理可以与DIoU/CIoU损失结合使用，这两个损失一方面优化IoU，一方面指引中心点的学习，而中心点距离学得越好，应该对这种后处理思想的执行越有利.

缺点：

  1. 依然是顺序处理模式，运算效率低.
  2. DIoU的计算比IoU更复杂一些，这会降低运算效率.
  3. 在保持NMS阈值不变的情况下，使用DIoU-NMS会导致每次迭代剩余更多的框，这会增加迭代轮数，进一步降低运算效率. (经本人实测，DIoU-NMS是Traditional NMS 起码1.5倍耗时)

7. 总结

  1. 加权平均法通常能够稳定获得精度与召回的提升.
  2. 定位优先法，方差加权平均法与自适应阈值法需要修改模型，不够灵活.
  3. 中心点距离法可作为额外惩罚因子与其他NMS变体结合.
  4. 得分惩罚法会改变box的得分，打破了模型校准机制.
  5. 运算效率的低下可能会限制它们的实时应用性.

8. 参考文献

Last modification：July 14th, 2020 at 09:53 pm
© 允许规范转载