论文:Context Encoding for Semantic Segmentation - CVPR2018
作者:Hang Zhang, Kristin Dana, Jianping Shi et.al
团队: Rutgers University, Amazon Inc, SenseTime, CUHK
Github - zhanghang1989/PyTorch-Encoding
Docs - Encoding Documentation
基于 FCN 的语义分割已经取得了很多提升,尤其是采用了 Dilated/Atrous Conv,Multi-scale features 以及 refining boundaries.
而该论文主要是探索在语义分割中 全局上下文信息(global contextual information) 的影响,提出了 上下文编码模块(Context Encoding Module),该模块可以捕捉场景的语义上下文信息,并选择性的突出类别相关的特征图(class-dependent features).

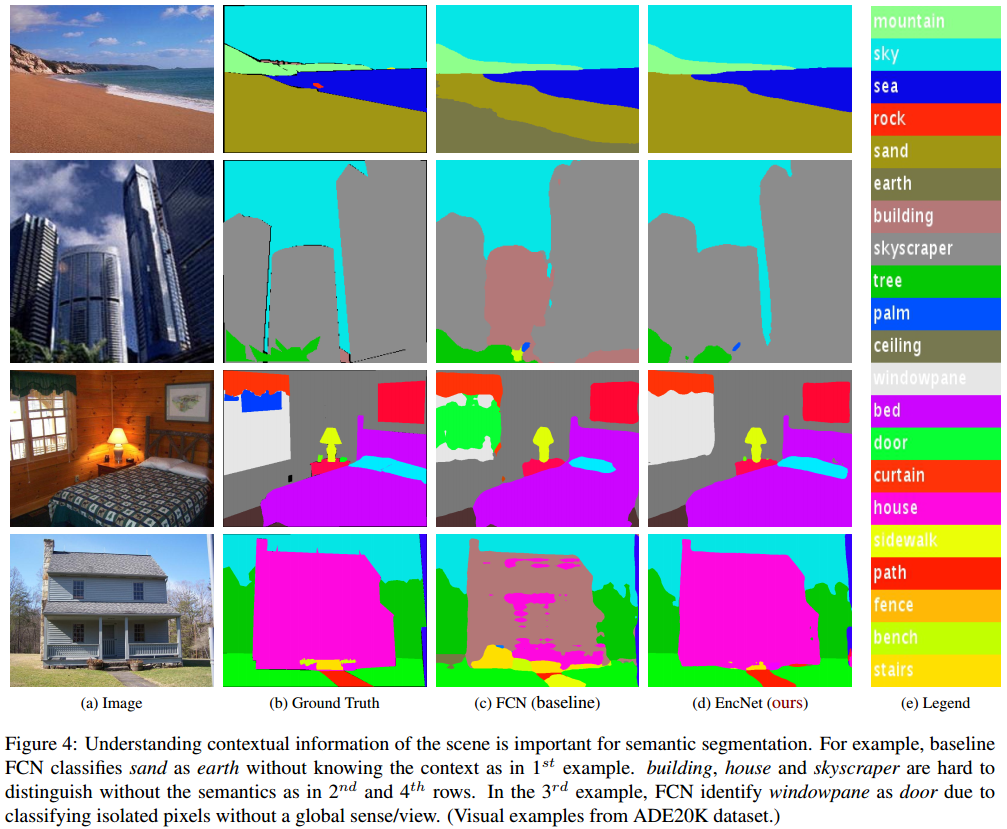
Fig 1. 精确的像素级场景标注的语义分割算法示例. 即使是人工标注,该任务也是很具挑战性的, 然而,基于场景上下文信息缩小可能类别的数量,有助于进行标注. 基于此,引入 Context Encoding Module.
论文主要贡献点:
[1] - Context Encoding Module 以及 Semantic Encoding Loss(SE-Loss).
Context Encoding Module 作为 Encoding Layer 整合进网络,用于捕捉全局上下文信息以及突出类别相关的特征图. 例如,可以不用关注室内场景出现车辆的概率.
语义分割中标准的训练过程是只采用像素级的分割 loss,其并未利用到场景的全局上下文信息. 这里提出 SE-Loss,对网络训练进行正则化,其使得网络预测场景中目标类别的存在,更有助于网络对于语义上下文信息的学习.
SE-Loss 与像素级 loss 的不同之处还在于,SE-Loss 不受目标物体大小的影响,其对于大目标物体和小目标物体的贡献一致对待(实际上,其对于小目标往往具有提升效果.)
[2] - Context Encoding Network(EncNet)
基于预训练的 ResNet,加入 Context Encoding Module 模块,其中还采用了 dilation 策略.
另外,还开源了 synchronized multi-GPU Batch Normalization 和 memory-efficient Encoding Layer 的 pytorch 实现.
1. EncNet
EncNet 网络结构如图:
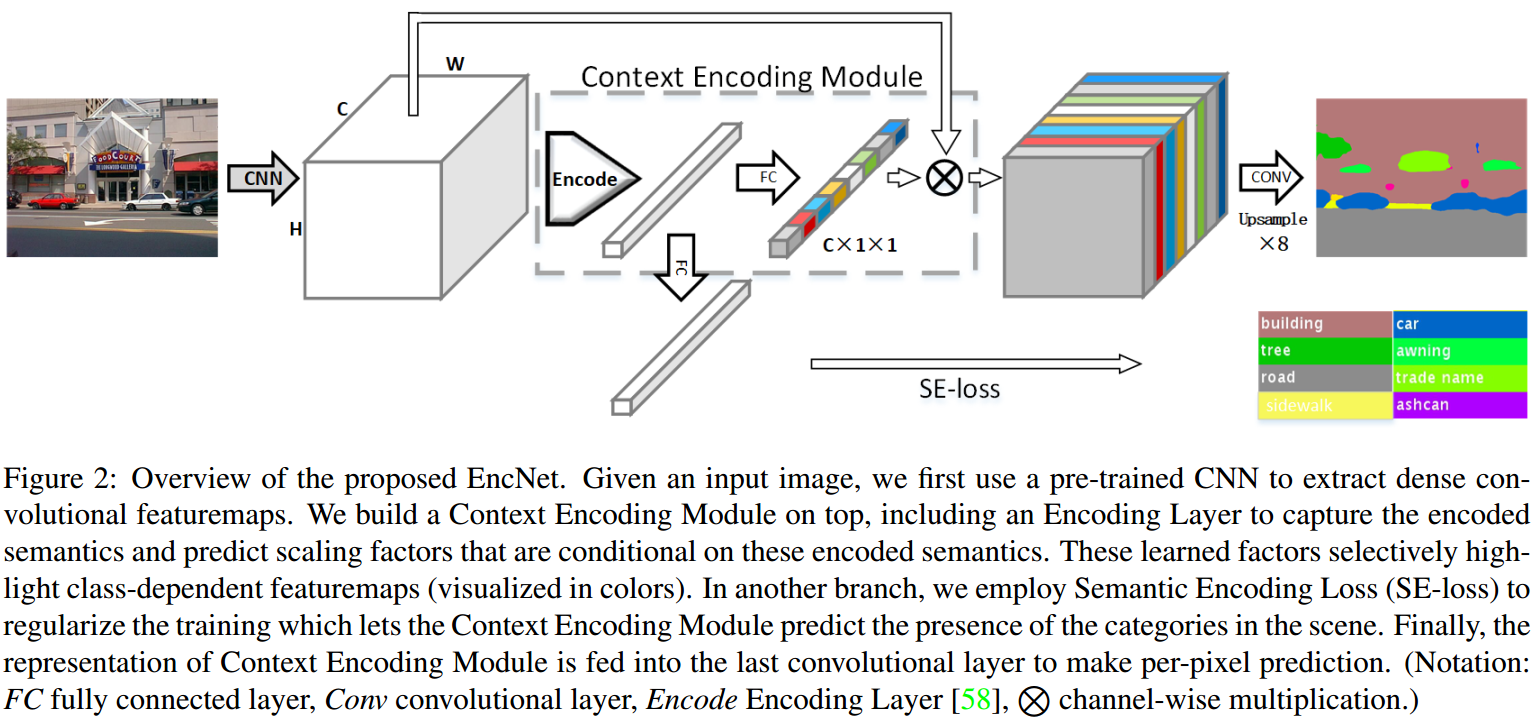
Fig2. EncNet 结构. (FC - 全连接层;Conv-卷积层;Encode-Encoding Layer;$\otimes$ - 逐通道相乘.)
给定输入图片,首先采用预训练的 CNN,提取卷积特征图;
然后,构建 Context Encoding Module,其包括 Encoding Layer 用以捕捉编码的语义信息(类似于BoW 的 codewords),并预测关于编码的语义信息的缩放因子(类似于BoW的 coefficients 系数). 学习得到的缩放因子可以有选择性的关注类别相关的特征图(Fig2 图颜色化表示的部分).
另一个网络分支,采用 SE-Loss 正则化网络训练,使得 Context Encoding Module 预测场景中存在的目标类别.
最后,Context Encoding Module 输出的特征表示被送入最后的卷积层,以得到像素级的预测.
1.1. Semantic Encoding Loss(SE-Loss)
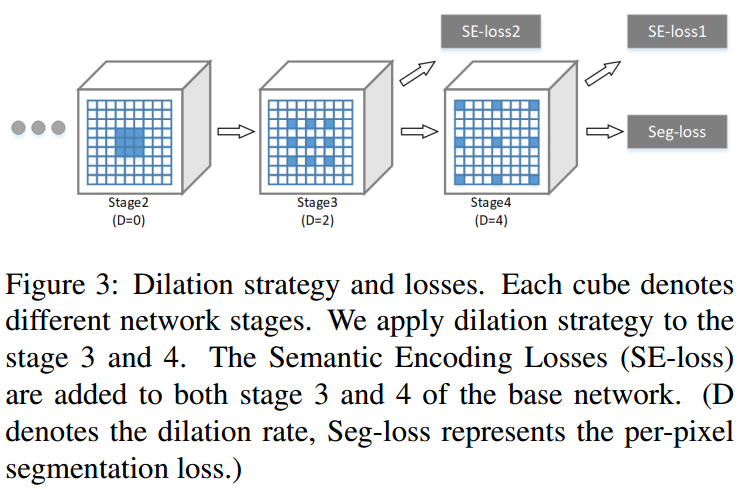
EncNet 的构建采用了 dilated 策略,如下图,在Stage3 和 Stage 4 采用了 dilation 卷积. 同时,添加了新的独立分支,以最小化 SE-Loss 正则化网络训练,其采用 encoded semantics 作为输入,输出预测的是物体类别是否存在.
语义分割问题的标准训练过程中,网络是对独立的像素进行学习(给定输入图像和对应的 GT labels,计算逐像素的交叉熵损失函数). 因此,网络很难理解带有全局信息的上下文内容.
SE-Loss(Semantic Encoding Loss) 作为新增的网络训练正则化损失函数,其是在 Encoding Layer 的输出端,新加一个全连接层和 sigmoid 激活函数,以对场景中物体类别存在的可能性进行预测,其后采用的是 BCE-Loss(Binary Cross Entropy Loss).
SE-Loss 对比于 PSPNet 的辅助 loss,类似,但计算代价更小.
SE-Loss 的 GT 是由 GT segmentation mask 直接生成的.
在开源的实现里,SE-Loss 如:
import torch
import torch.nn.functional as F
import torch.nn as nn
from torch.autograd import Variable
import numpy as np
class SegmentationLosses(nn.CrossEntropyLoss):
"""2D Cross Entropy Loss with Auxilary Loss"""
def __init__(self,
se_loss=False,
se_weight=0.2,
nclass=-1,
aux=False,
aux_weight=0.4,
weight=None,
ignore_index=-1):
super(SegmentationLosses, self).__init__(weight, None, ignore_index)
self.se_loss = se_loss
self.aux = aux
self.nclass = nclass
self.se_weight = se_weight
self.aux_weight = aux_weight
self.bceloss = nn.BCELoss(weight)
def forward(self, *inputs):
if not self.se_loss and not self.aux:
return super(SegmentationLosses, self).forward(*inputs)
elif not self.se_loss:
pred1, pred2, target = tuple(inputs)
loss1 = super(SegmentationLosses, self).forward(pred1, target)
loss2 = super(SegmentationLosses, self).forward(pred2, target)
return loss1 + self.aux_weight * loss2
elif not self.aux:
pred, se_pred, target = tuple(inputs)
se_target = self._get_batch_label_vector(target, nclass=self.nclass).type_as(pred)
loss1 = super(SegmentationLosses, self).forward(pred, target)
loss2 = self.bceloss(torch.sigmoid(se_pred), se_target)
return loss1 + self.se_weight * loss2
else:
pred1, se_pred, pred2, target = tuple(inputs)
se_target = self._get_batch_label_vector(target, nclass=self.nclass).type_as(pred1)
loss1 = super(SegmentationLosses, self).forward(pred1, target)
loss2 = super(SegmentationLosses, self).forward(pred2, target)
loss3 = self.bceloss(torch.sigmoid(se_pred), se_target)
return loss1 + self.aux_weight * loss2 + self.se_weight * loss3
@staticmethod
def _get_batch_label_vector(target, nclass):
# target is a 3D Variable BxHxW, output is 2D BxnClass
batch = target.size(0)
tvect = Variable(torch.zeros(batch, nclass))
for i in range(batch):
hist = torch.histc(target[i].cpu().data.float(),
bins=nclass,
min=0,
max=nclass-1)
vect = hist>0
tvect[i] = vect
return tvect1.2. 实现细节
[1] - 在预训练网络的 stage 3 和 stage 4 采用 dilation 策略,输出尺寸(output size )为输入的 1/8. 采用双线性插值(bilinear interpolation)上采样 8x,得到输出预测,以计算 loss.
[2] - 学习率策略 $lr = baselr *(1 - \frac{iter}{total\_iter})^{power}$.
[3] - 训练时,随机打乱训练样本,并丢弃最后一个 mini-batch.
[4] - 数据增强,随机翻转图片,在[0.5, 2]区间缩放图片,随机旋转图片 [-10, 10] 度,最后裁剪图片为固定尺寸(zero padding).
[5] - 测试时,多尺度预测结果求平均.
2. Context Encoding Module
2.1. Context Encoding
对于在大规模数据集,如 ImageNet,预训练的网络所提取的图片特征图编码了场景中目标物体的丰富信息.
这里采用 Encoding Layer 对特征图处理,捕捉得到全局语义上下文信息. 记 Encoding Layer 的输出为 encoded semantics.
为了能够利用 encoded semantics,会同时预测缩放因子集合以有选择性地关注类别相关的特征图.
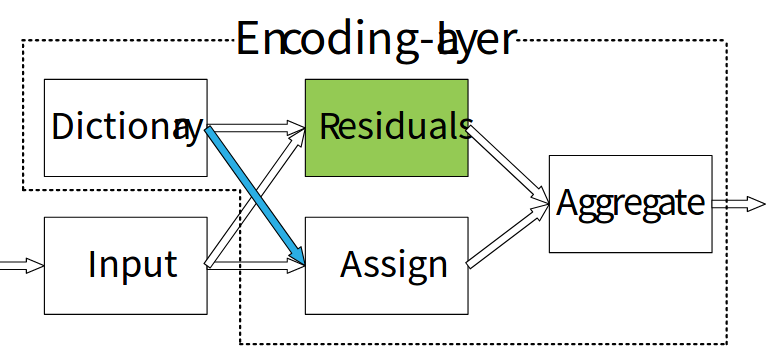
Encoding Layer 学习得到了一个包含数据集语义上下文信息的内在字典(inherent),并输出包含丰富上下文信息的残差编码器(residual encoders).
Encoding Layer:
[1] - 输入:将 $C \times H \times W$ 的特征图看作为 C 维的输入特征 $X = \lbrace x_1, ..., x_N \rbrace$,其中, N 为由 $H \times W$ 给定的特征总数.
[2] - Encoding Layer 学习得到一个 inherent codebook: $D \in \lbrace d_1, ..., d_K \rbrace$,包含 K 个 codewords(visual centers);以及对应的 visual centers 缩放因子集合:$S = \lbrace s_1, ..., s_K \rbrace$.
[3] - 输出:Encoding Layer 通过聚合带有 soft-assignment weights $e_k \sum _{i=1}^N e_{ik}$ 的残差, 以输出残差编码(residual encoder). 其中,
$$ e_{ik} = \frac{exp(-s_k ||r_{ik}||^2)}{\sum_{j=1}^K exp(-s_j||r_{ij}||^2)}r_{ik} $$
残差(residuals) 的计算为:$r_{ik} = x_i -d_k$.
这里对于 encoder 采用聚合(aggregation),而不是连接(concatenation) 处理. 即:
$$ e = \sum_{k=1}^K \phi(e_k) $$
其中,$\phi$ 表示 Batch Normalization 和 ReLU 处理,避免导致 K 个独立的 encoders 被排序,同时降低特征表示的维度.
输出的 encoders 为: $E = \lbrace e_1, ..., e_K \rbrace$.
如图:
2.1.1. Encoding 的 PyTorch 实现
class Encoding(Module):
def __init__(self, D, K):
super(Encoding, self).__init__()
# init codewords and smoothing factor
#D-dim of features
#K-num of codeswords
self.D, self.K = D, K
self.codewords = Parameter(torch.Tensor(K, D), requires_grad=True)
self.scale = Parameter(torch.Tensor(K), requires_grad=True)
self.reset_params()
def reset_params(self):
std1 = 1./((self.K*self.D)**(1/2))
self.codewords.data.uniform_(-std1, std1)
self.scale.data.uniform_(-1, 0)
def forward(self, X):
# input X is a 4D tensor
assert(X.size(1) == self.D)
B, D = X.size(0), self.D
if X.dim() == 3:
# BxDxN => BxNxD
X = X.transpose(1, 2).contiguous()
elif X.dim() == 4:
# BxDxHxW => Bx(HW)xD
X = X.view(B, D, -1).transpose(1, 2).contiguous()
else:
raise RuntimeError('Encoding Layer unknown input dims!')
# assignment weights BxNxK
A = F.softmax(scaled_l2(X, self.codewords, self.scale), dim=2)
# aggregate
E = aggregate(A, X, self.codewords)
return E
def __repr__(self):
return self.__class__.__name__ + '(' \
+ 'N x ' + str(self.D) + '=>' + str(self.K) + 'x' \
+ str(self.D) + ')' [1] - 输入: $X \in R^{B \times N \times D}$ 或 $X \in R^{B \times D \times H \times W}$. 其中,B-batch,N-features 总数
[2] - 输出: $E \in R^{B \times K \times D}$
[3] - 使用示例:
import encoding
import torch
import torch.nn.functional as F
from torch.autograd import Variable
B,C,H,W,K = 2,3,4,5,6
X = Variable(torch.cuda.DoubleTensor(B,C,H,W).uniform_(-0.5,0.5), requires_grad=True)
layer = encoding.Encoding(C,K).double().cuda()
E = layer(X)2.2. Featuremap Attention
对于 Encoding Layer 输出的 encoded semantics 的使用,论文预测特征图的缩放因子作为反馈,以判断是重视还是忽视类别相关的特征图.
具体地,
首先,在 Encoding Layer 的输出端接 FC 层和 sigmoid 激活函数,以输出预测的缩放因子 $\gamma = \delta (We)$,其中,W 表示网络层权重,$\delta$ 表示 sigmoid 激活函数.
然后,其输出由 $Y = X \otimes \gamma$ 得到,计算的是,输入特征图 X 和缩放因子 $\gamma$ 间的逐通道相乘(channel wise multiplication).
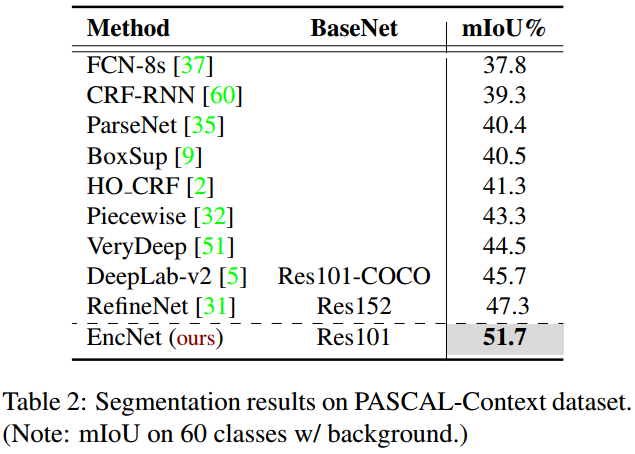
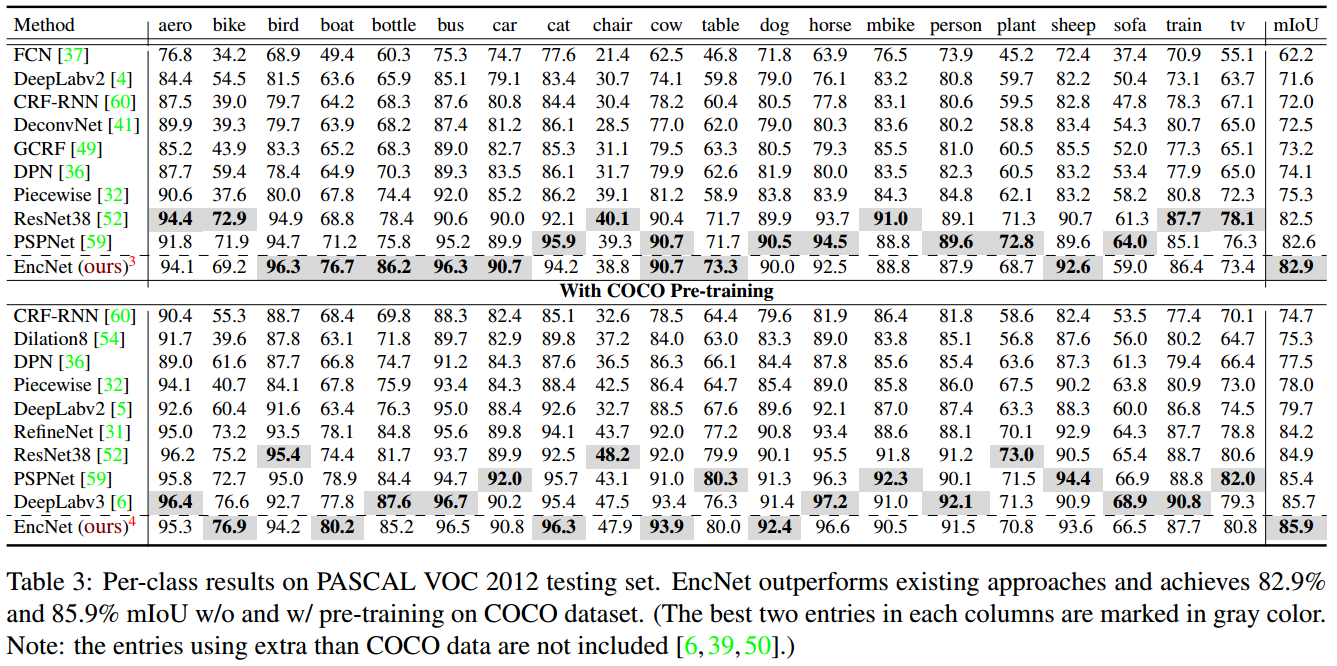
3. Results
简单如,