原文:计算机图形学(四)-MVP变换之视图(View)变换 - 2021.07.21
作者:点燃火柴 - CSDN
1. MVP变换
把三维空间中的物体投影到二维平面上展示,需要经过MVP变换,MVP变换指的是:模型变换(model)、视图变换(view)、投影变换(projection)。可以设想一下拍照的过程,通常需要三步,人物摆pose、调整相机、按下快门拍照。把三维物体投影到二维平面则需要经过MVP变换, MVP变换与拍照的类比关系如下:
- 摆Pose - 模型变换
- 调整相机位置 - 视图变换
- 拍照 - 投影变换
模型变换指的是物体的缩放、平移、旋转等变换, 视图变换 主要指如何确立相机位置, 投影变换,就是最后最重要的一步,把三维图形投影到二维平面
2. 视图变换(view)
视图变换主要说明
2.1. 相机介绍
视图变换又称相机变换,主要学习如何确定一个相机。
确定相机需要三个因素,相机位置、视线方向、上方向
- 位置,指的是相机摆在哪里
- 视线方向,指的是相机朝哪个方向看去
- 上方向,这是一个很重要的因素,用来保证相机无法绕z轴旋转
在图形学中相机默认是:相机放在原点,相机方向是-Z方向,上方向是Z轴
2.2. 视图变换矩阵推导
假设有一个相机,相机位置是 e,视线方向是 g,上方向是 t,现在需要把它的位置平移到原点位置,视线方向变为-Z,上方向变为Y
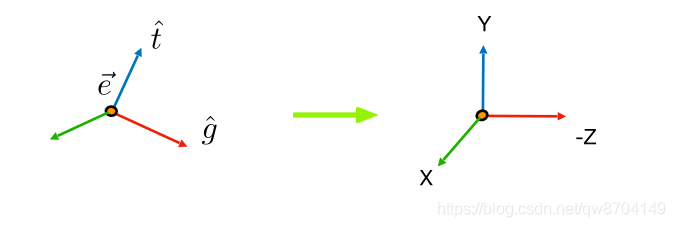
需要怎么做:
[1] - 位置从e平移到坐标原点
[2] - 视线方向从 g 旋转到-Z
[3] - 上方向从 t 旋转到Y,这时g × t 也自动与X重合了
上面一系列的操作如何用矩阵表示,我们想要的操作是先平移再旋转,但是矩阵变换默认是先旋转再平移(先进行线性变换再进行仿射变换),要让相机先平移在旋转,就要按从右到左的顺序让矩阵相乘,表示如下:
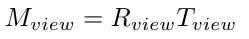
相机位置从e平移到坐标原点的平移矩阵如下
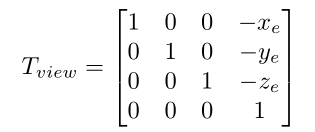
把相机的视线方向 g 旋转到与-Z重合,上方向 t 旋转到与Y重合,g × t 与X重合比较困难,于是我们反向思考,把-Z旋转到与 g 重合,Y旋转到与 t 重合就会容易一些。视图旋转矩阵的逆矩阵如下
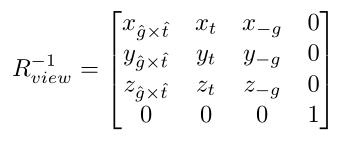
我们知道旋转矩阵是正交矩阵,一个正交矩阵的逆矩阵等于它的转置矩阵,那么只要把逆矩阵转置即可得到想要的视图旋转矩阵
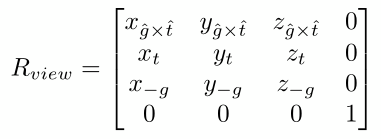
2.3. 视图变换矩阵
将上面的旋转矩阵和平移矩阵代入就得到 视图变换矩阵
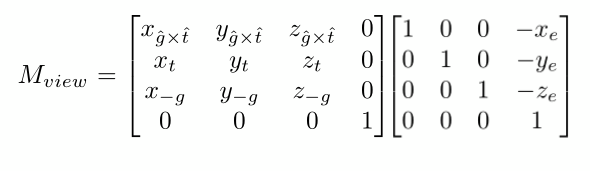
物理中有个理论是相对运动,对于视图变换同样适用,例如,物体不变相机逆时针旋转45度,与相机不变物体做顺时针旋转45度,这时得到的视图是一样的。按照这个思路,模型变换和视图变换其实可以做同样的事情,通常为了实现一个物体运动的效果,可以直接让物体动(模型变换),也可以物体不动,相机做相反的运动(视图变换),实际开发中可以根据需要灵活应用