原文:计算机图形学(一)-向量、向量加减法、向量的点积(乘)及应用、向量的叉积(乘)及应用 - 2021.05.08
作者:点燃火柴 - CSDN
1. 向量
向量 是用来表示既有大小又有方向的量,不过向量在空间中没有具体的位置,通常用一个加粗的小写字母来表示一个向量,或者不加粗顶上带有小箭头的小写字母来表示
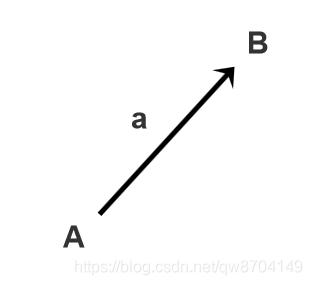
由 A 点指向 B 点的一个有向线段,称为向量 a
a = B - A 用有向线段的结束点B减去起始点A就得到这个向量 a
|a| 表示向量a的长度
â 表示单位向量,â = a / |a|
2. 向量的矩阵表示
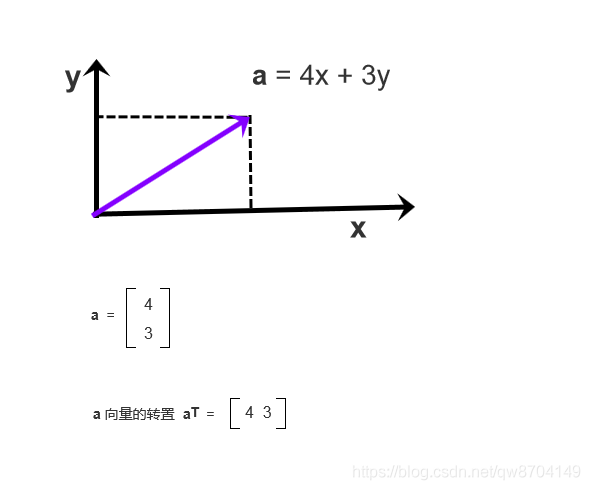
如上图中向量 a 在X轴和Y轴的分量分别为4和3,那么可以用这两个分量以矩阵的形式表示这个向量,
上图中纵向排列的被称为列向量,转置后被称为行向量,它们都表示同一个向量
3. 向量加法
向量加法不同于普通数学加法,它还具有方向属性,因此向量加法采用三角形定则或平行四边形定则计算
3.1. 三角形定则
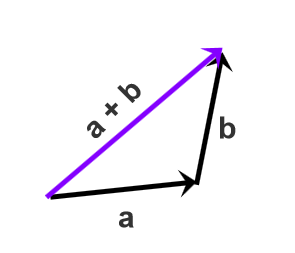
将各个向量依次首尾顺次相接,结果为第一个向量的起点指向最后一个向量的终点
向量a加向量b,将a和b首尾相连后,由a的起点指向b的终点,就是 a + b
3.2. 平行四边形定则
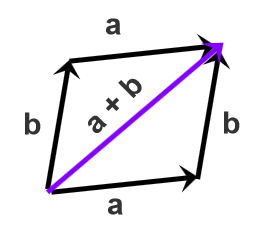
将两个向量平移至公共起点,以这两个向量绘制平行四边形,从公共起点到公共终点的向量为相加结果
将向量a和向量b的起点移到左下角的公共起点,然后以这两个向量绘制平行四边形,由公共起点指向公共终点就是 a + b
4. 向量减法
向量减法一般使用三角形定则运算
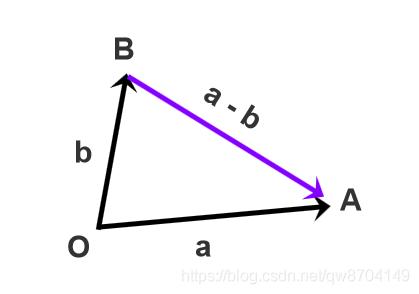
将两个向量平移至公共起点O,从减数向量的终点B指向被减向量的终点A为相减结果
将向量a和向量b的起点移到左下角的公共起点O,从点B指向点A的向量就是 a - b
向量相减也可以当做加上一个负的向量,负向量代表大小相等方向相反的向量
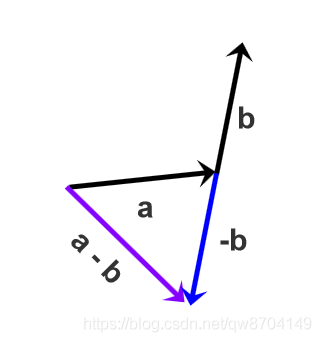
将向量相减当做加上一个负的向量,即 a - b = a + (-b)
5. 向量的点积(乘)
5.1. 点积
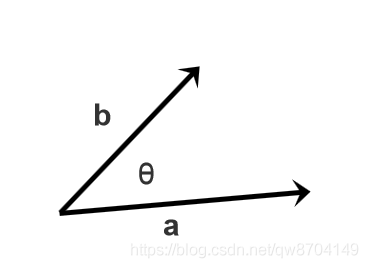
两个向量的点积(乘),记作 $\boldsymbol{a} \cdot \boldsymbol{b}$.
两个向量的点积等于两个向量的长度相乘再乘以两个向量夹角的余弦值:
$$ \boldsymbol{a} \cdot \boldsymbol{b} = |\boldsymbol{a}| |\boldsymbol{b}| \boldsymbol{cos} \theta $$
两个向量夹角的余弦值等于两个向量的点积除以两个向量的长度的积:
$$ \text{cos} \theta = \frac{\boldsymbol {a} \cdot \boldsymbol{b}} { |\boldsymbol{a}| |\boldsymbol{b}| } $$
两个向量夹角的余弦值也等于两个向量的单位向量的点乘:
$$ \boldsymbol{cos} \theta = \hat{\boldsymbol{a}} \cdot \hat{\boldsymbol{b}} $$
5.2. 向量点乘的矩阵表示法
二维向量点乘矩阵表示法:
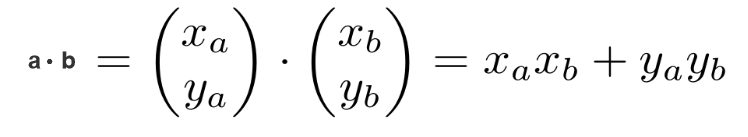
三维向量点乘矩阵表示法:
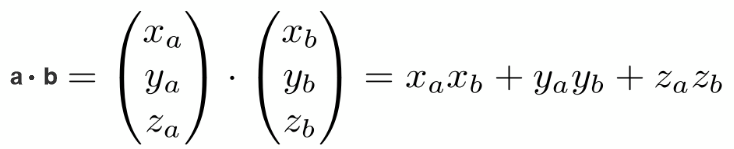
5.3. 向量点乘适用的运算定律
[1] - 交换律 a · b = b · a
[2] - 分配律 a · (b + c) = a · b + a · c
[3] - 结合律 (ka) · b = a · (kb) = k(a · b)
5.4. 一个向量投影到另一个向量
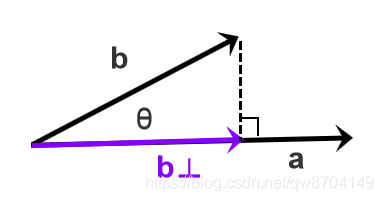
向量 b⊥ 为向量 b 在向量 a 上的投影向量
向量 b⊥ 与向量 a 方向相同,若向量 a 是单位向量则有,
$$ \boldsymbol{b} ⊥ = k \hat{\boldsymbol{a}} $$
通过三角函数的性质,可以得出:
$$ |\boldsymbol{b} ⊥| = |\boldsymbol{b}| \boldsymbol{cos} \theta $$
5.5. 向量点乘的应用
5.5.1. 计算两个向量的夹角
已知两个向量,可以通过以下公式求出cosθ, 然后通过反余弦函数计算出夹角θ:
$$ \text{cos} \theta = \frac{\boldsymbol {a} \cdot \boldsymbol{b}} { |\boldsymbol{a}| |\boldsymbol{b}| } $$
5.5.2. 判断两个向量的方向
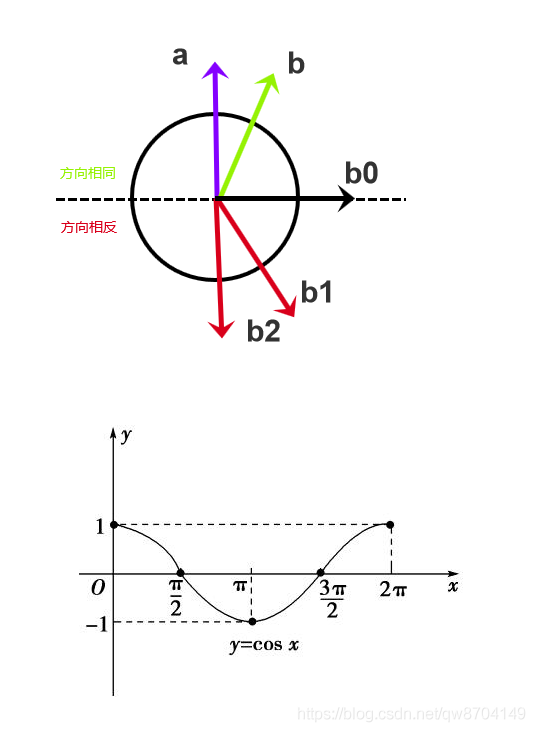
先将向量a和向量b做归一化处理:
$$ \text{cos} \theta = \frac{\boldsymbol {a} \cdot \boldsymbol{b}} { |\boldsymbol{a}| |\boldsymbol{b}| } $$
可变换为:
$$ \boldsymbol{a} \cdot \boldsymbol{b} = \boldsymbol{cos} \theta $$
如果 a · b 等于1,说明夹角是0度或360度,两个向量重合
如果 a · b 大于0小于1,说明夹角在0度到90度之间或270度与360度之间,即向量 a 与向量 b 是相同的方向
如果 a · b 等于0,说明夹角是90度或270度,两个向量垂直
如果 a · b 小于0大于-1,说明夹角在90度到270度之间 (不包括180度),即向量 a 与向量 b 方向相反
如果 a · b 等于-1,说明夹角是180度,两个向量方向相反,如上图中向量 a 与向量 b2
5.5.3. 判断两个向量是否接近
判断两个向量是否接近,其实是判断方向的更近一步的应用,上面提到如果两个向量点乘等于1说明两个向量重合,那么两个向量点乘越接近1说明两个向量越接近,这个性质在光反射模型中计算高光时非常有用,先简单说一下,在近似镜面反射中,如果反射光的方向与人眼观察方向很接近,那么在一定的范围内可以观察到物体表面的高光
6. 向量的叉积(乘)
6.1. 叉积
两个向量的叉积(乘)的结果是一个向量,记作 $\boldsymbol{c} = \boldsymbol{a} \times \boldsymbol{b}$
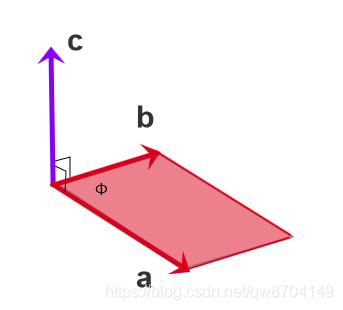
6.2. 向量叉乘结果方向确定
使用右手螺旋法则确定向量 c 的方向,首先做出点赞手势,四指方向从向量 a 旋转到向量 b,这时拇指方向就是向量 c 的方向
6.3. 向量叉乘的一些性质
[1] - 向量 a 叉乘向量 b 的结果为向量 c. 向量 c 垂直于向量 a, 向量 c 垂直于向量 b,继而向量 c 垂直于向量 a与向量 b组成的平面
[2] - 向量 a 叉乘向量 b 等于负的向量 b 叉乘向量 a,a x b = -b x a
[3] - 两个向量的叉乘的模长等于两个向量的模长相乘再乘以两个向量夹角的正弦值 |a x b| = |a| |b| sinΦ
[4] - 两个向量平行,因为sin0 = 0,则得到 |a x b| = 0 ,0 代表0向量. |a x b| 的值是以向量 a 和向量 b 为边组成的平行四边形的面积
6.4. 向量叉乘矩阵表示法
向量的叉乘可以写成一个向量对应的矩阵乘以另一个向量:

通过矩阵乘法规则推理得出下面结果
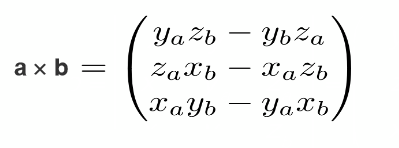
6.5. 向量叉乘适用的运算定律
[1] - 分配律 a x (b + c) = a x b + a x c
[2] - 结合律 a x (kb) = k(a x b)
6.6. 向量叉乘的应用
6.6.1. 判断一个向量在另一个的左侧还是右侧
根据右手螺旋定则,如果向量 a 叉乘向量 b 的结果 > 0,右手旋转时时从 a 向量转向 b 向量,所以 b 向量在 a 向量的左侧,若叉乘结果< 0,则 b 向量在 a 向量的右侧
[1] - 向量 a 叉乘向量 b > 0, b 向量在 a 向量的左侧
[2] - 向量 a 叉乘向量 b < 0, b 向量在 a 向量的右侧
6.6.2. 判断一个点是否在三角形内部
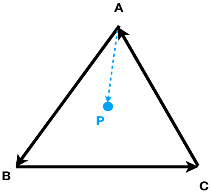
判断一个点是否在三角形内部的步骤:
[1] - 把三角形的三条边按一定的顺序依次连接,组成三个向量,上图中是按逆时针方向连接
[2] - 取其中的一个向量AB,构造一个向量AP,从向量的起点A指向P点,向量AB叉乘向量AP,结果 > 0,所以 AP 在 AB 的左侧
[3] - 取下一个向量BC,计算向量BC叉乘向量BP,结果 > 0, 得到BP 也在 BC 的左侧
[4] - 取下一个向量CA,计算向量CA叉乘向量CP,结果 > 0, 得到CP 也在 CA 的左侧
[5] - 由第2,3,4步的结果推断出P点在三角形内部,如果第2,3,4步中有一个结果有一个不在左侧则P点不在三角形内部
如果开始连接三角形时按逆时针方向连接,即三条边的向量为AC,CB,BA,则第2,3,4步叉乘的结果都<0,说明P点与三条边的向量起点组成的向量均在对应边向量的一侧,也可以判断P点在三角形内部,实际上判断点是否在三角形内部的依据是,边向量的起点与要判断的点组成的向量是否在三个边向量的同一侧.