1. 什么是正则化?
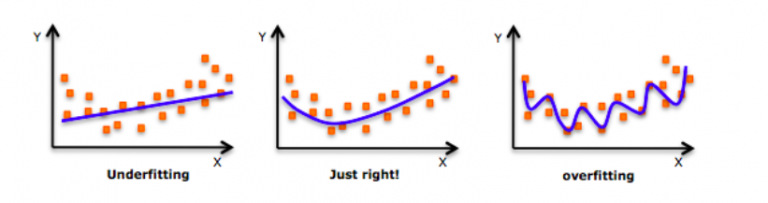
当向右移时,模型试图从训练数据中很好地学习细节和噪声,这最终导致在看不见的数据上表现不佳。
也就是说,当模型向右移动时,模型的复杂度增加,使得训练误差减小,而测试误差没有减小。如下图所示。
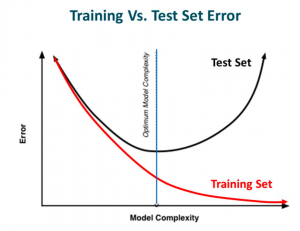
如果以前建立过神经网络,就知道它们有多复杂。这使得他们更容易过度拟合。

正则化是一种对学习算法稍加修改以使模型具有更好的泛化能力的技术。这反过来也提高了模型在看不见的数据上的性能。
2. 正则化如何帮助减少过拟合?
假设一个神经网络对训练数据进行了过度拟合,如下图所示。
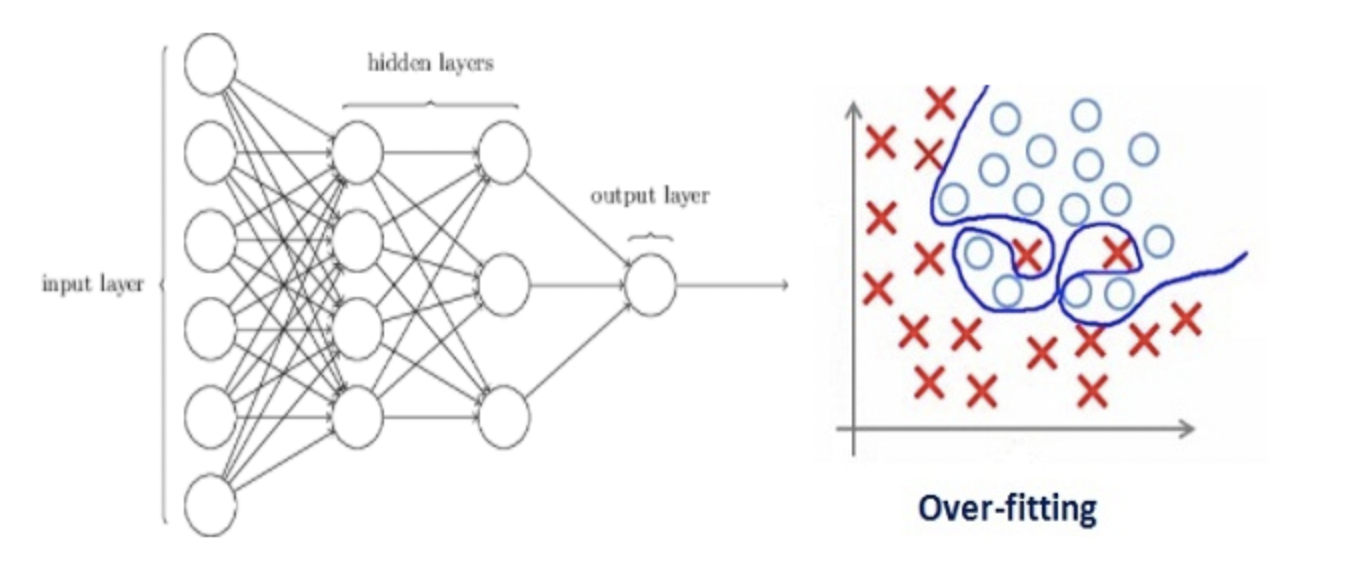
如果研究过机器学习中正则化的概念,会有一个想法,正则化惩罚系数。在深度学习中,它实际上惩罚节点的权重矩阵。
假设正则化系数非常高,以至于一些权重矩阵几乎等于零。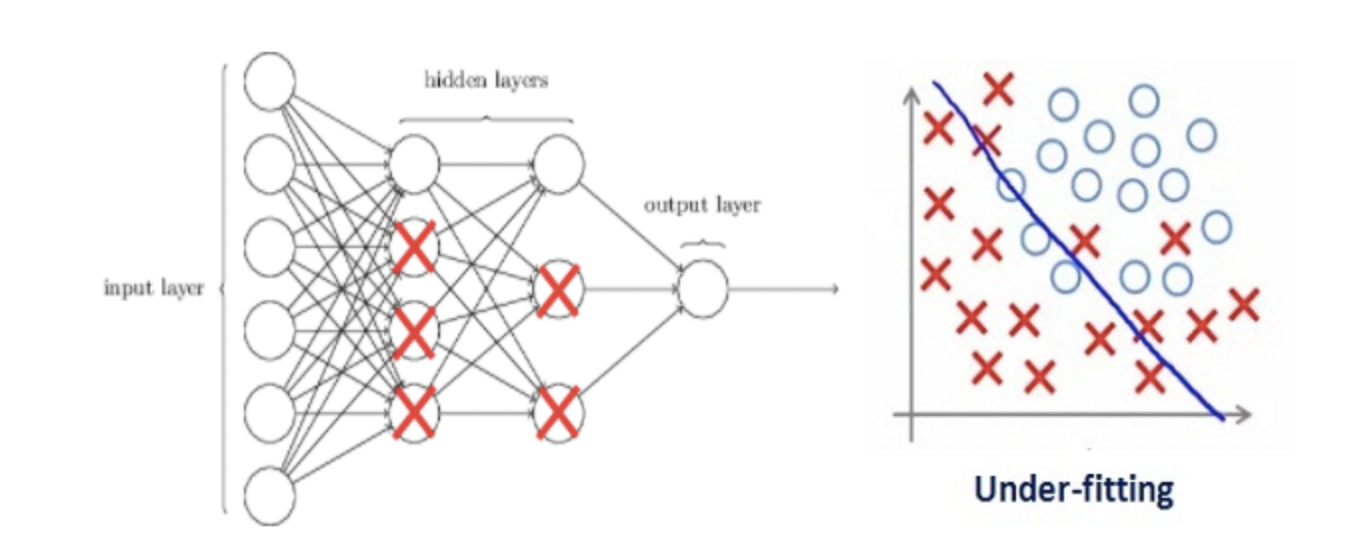
这将导致更简单的线性网络和训练数据的轻微欠拟合。
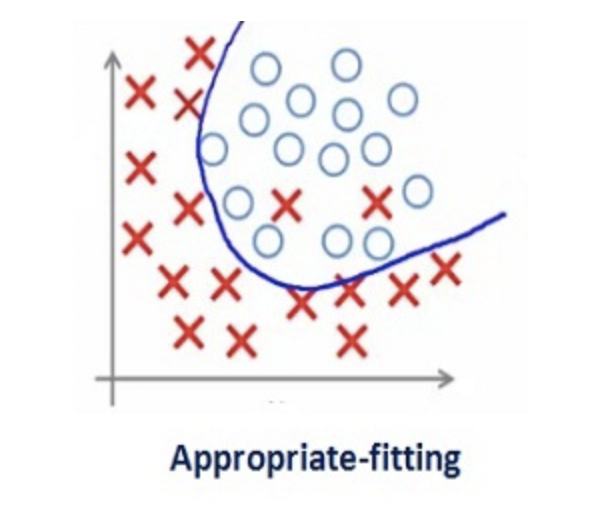
如此大的正则化系数值并不是很有用。我们需要优化正则化系数的值,以获得如下图所示的良好拟合模型。
正则化可以避免算法过拟合,过拟合通常发生在算法学习的输入数据无法反应真实的分布且存在一些噪声的情况。过去数年,研究者提出和开发了多种适合机器学习算法的正则化方法,如数据增强、L2 正则化(权重衰减)、L1 正则化、Dropout、Drop Connect、随机池化和早停等。
除了泛化原因,奥卡姆剃刀原理和贝叶斯估计也都支持着正则化。根据奥卡姆剃刀原理,在所有可能选择的模型中,能很好解释已知数据,并且十分简单的模型才是最好的模型。而从贝叶斯估计的角度来看,正则化项对应于模型的先验概率。
3. L1 和 L2 正则化
L1 和 L2 正则化是最常用的正则化方法。
L1 正则化向目标函数添加正则化项,以减少参数的绝对值总和;
而 L2 正则化中,添加正则化项的目的在于减少参数平方的总和。
根据之前的研究,L1 正则化中的很多参数向量是稀疏向量,因为很多模型导致参数趋近于 0,因此它常用于特征选择设置中。机器学习中最常用的正则化方法是对权重施加 L2 范数约束。
标准正则化代价函数如下:
$$\theta= arg min_{\theta} \frac{1}{N}\sum_{i=1}^{N}(L(\hat y_{i},y)+\lambda R(w))$$
其中正则化项 R(w) 是:
$$R_{L_{2}}(w)=||W||_{2}^2$$
另一种惩罚权重的绝对值总和的方法是 L1 正则化:
$$R_{L_{1}}(w)=||W||_{1}$$
L1 正则化在零点不可微,因此权重以趋近于零的常数因子增长。很多神经网络在权重衰减公式中使用一阶步骤来解决非凸 L1 正则化问题。L1 范数的近似变体是:
$$||W||_{1}=\sum_{k=1}^{Q}\sqrt{w_{k}^2+\epsilon}$$
另一个正则化方法是混合 L1 和 L2 正则化,即弹性网络罚项。
整个最优化问题从贝叶斯观点来看是一种贝叶斯最大后验估计,其中正则化项对应后验估计中的先验信息,损失函数对应后验估计中的似然函数,两者的乘积即对应贝叶斯最大后验估计的形式
3.1. 贝叶斯推断分析法
针对L1范数和L2范数还有结论:
- L1范数相当于给模型参数$\theta$设置一个参数为$\frac{1}{\alpha}$的零均值拉普拉斯先验分布
- L2范数相当于给模型参数$\theta$设置一个协方差$\frac{1}{\alpha}$的零均值高斯先验分布
[1] - L2范数相当于给模型参数$\theta$设置一个零均值高斯先验分布
以线性模型为例,结论可以推广到任意模型,线性模型方程可以表示为:
$$Y=\theta^TX+\epsilon$$
其中$\epsilon$表示误差,$\epsilon \sim N(0,\sigma^2)$,$\theta_{i} \sim N(0,\tau^2)$,则有:
$$p(\epsilon_{i})=\frac{1}{\sqrt{2 \pi \sigma^2}}exp(- \frac{\epsilon_{i}^2}{2\sigma^2})$$
$$p(y_{i}|x_{i};\theta)=\frac{1}{\sqrt{2 \pi \sigma^2}}exp(-\frac{(y_{i}-\theta^Tx_{i})^2}{2\sigma^2})$$
计算最大后验估计:
$$arg max_{\theta}lnL(\theta)=argmax_{\theta}(ln \prod_{i=1}^np(y_{i}|x_{i};\theta)+lnp(\theta))$$
$$=ln\prod_{i=1}^n \frac{1}{\sqrt{2 \pi \sigma^2}} exp(-\frac{(y_{i}-\theta^Tx_{i})^2}{2\sigma^2})+ln\prod_{j=1}^d \frac{1}{\sqrt{2 \pi \tau^2}} exp(- \frac{\theta_{j}^2}{2\tau^2})$$
$$=-\frac{1}{2\sigma^2}\sum_{i=1}^n(y_{i}-\theta^Tx_{i})^2-\frac{1}{2\tau^2}\sum_{j=1}^d\theta_{j}^2+nln\sigma\sqrt{2\pi}-dln\tau \sqrt{2 \pi}$$
最大化上式,去掉负号,统一参数可以转化为:
$$arg min_{\theta}ln L(\theta)=\sum_{i=1}^n(y_{i}-\theta^Tx_{i})^2+\lambda \sum_{j=1}^d\theta_{j}^2$$
上式正好是线性回归问题在L2范数的代价函数,故验证了结论。
[2] - L1范数相当于给模型参数$\theta$设置一个拉普拉斯先验分布
以线性模型为例,结论可以推广到任意模型,同样假设$\epsilon \sim N(0,\sigma^2)$,$\theta_{i} \sim Laplace(0,b)$,则有:
$$arg max_{\theta}ln L(\theta)=ln\prod_{i=1}^n p(y_{i}|x_{i};\theta)+lnp(\theta)$$
$$=ln\prod \frac{1}{\sqrt{2\pi \sigma^2}}exp(-\frac{(y_{i}-\theta^Tx_{i})^2}{2\sigma^2})+ln\prod_{j=1}^d \frac{1}{2b}exp(-\frac{|\theta_{j}|}{b})$$
$$=\frac{1}{2\sigma^2}\sum_{i=1}^n (y_{i}-\theta^Tx_{i})^2-\frac{1}{b}\sum_{i=1}^n|\theta_{j}|-nln\sigma\sqrt{2\pi}-dln2b$$
最大化上式,去掉负号和统一参数,就变成了最小化:
$$arg min_{\theta} lnL(\theta)=\sum_{i=1}^n (y_i-\theta^T x_{i})+\lambda \sum_{j=1}^d|\theta_{j}|$$
上式正好是线性回归问题在L1范数正则下的代价函数,故验证了结论。
如果误差符合0均值的高斯分布,那么最大似然估计法的结果就是最小二乘法,这也是为何误差定义经常使用$\sum_{i=1}^n (y_{i}-\theta^Tx_{i})^2$的原因,因为这个公式是基于概率推导出来的