Softmax 函数是分类模型中常用的主要函数之一. 其最早是在机器学习中提出的.
Softmax 函数将输入作为一个固定长度为 d 的实值向量,并将其归一化为概率分布. 其易于理解和解释的,但其核心仍有值得深入弄明白之处,比如其实际实现、数值稳定性及应用.
1. 介绍
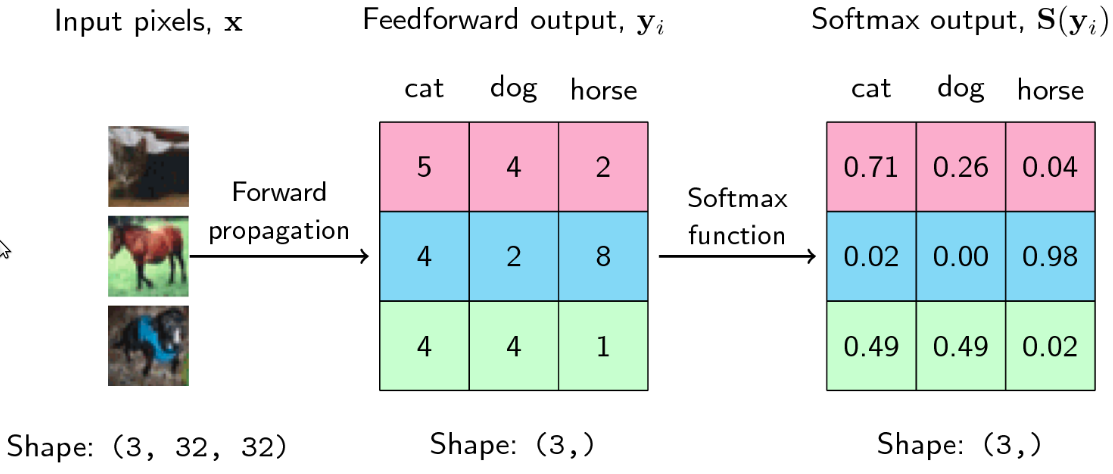
Softmax 是非线性函数,主要用于 multi-class classification 任务中分类器的输出端.
给定向量 $[x_1, x_2, x_3, ..., x_d]$,softmax 函数形式为:
$$ sm(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{d} e^{x_j}} $$
$i = 1, 2, ..., d$,d 为类别数量.
$\sum_{j=1}^{d} e^{x_j}$ 所有指数值的和,是一个归一化常数值,其有助于确保概率分布的特点,比如,
[1] - 数值之和必须是 1.
[2] - 每个值都在 [0, 1] 区间范围内.
例如,给定向量 $x = [10, 2, 40, 4]$,计算每个元素的 softmax值:
- 每个元素值的指数 $e^x = [e^{10}, e^2, e^{40}, e^4]$
- 计算元素值的指数值之和 $\sum e^x = e^{10} + e^2 + e^{40} + e^4 = 2.353...e^{17}$
- 每个元素的指数值除以全部元素的指数值之和 $sm(x) = [9.35762297e^{-17}, 3.13913279e^{-17}, 1.00000000e^{+00}, 2.31952283e^{-16}]$
其实现如:
import numpy as np
def softmax(x):
exp_x = np.exp(x)
sum_exp_x = np.sum(exp_x)
sm_x = exp_x/sum_exp_x
return sm_x
#
x = np.array([10, 2, 40, 4])
print(softmax(x))
#[9.35762297e-14 3.13913279e-17 1.00000000e+00 2.31952283e-16]问题:
- 从输出观察出了什么?
- 输出值之和是 1 吗?
2. Softmax 的数值稳定性
从上面 softmax 的概率值可以看出,当元素值范围非常大时,容易出现数值不稳定性. 比如,修改上面向量的第三个元素值为 10000,并重新计算 softmax:
x = np.array([10, 2, 10000, 4])
print(softmax(x))
#[0.0, 0.0, nan, 0.0]nan 表示 not-a-number,往往出现在过拟合(overflow) 和 欠拟和(underflow) 中. 但是,Softmax 为什么会输出这样的结果呢?是不能得到向量的概率分布吗?
问题: 能找出是什么所导致过拟合吗?
一个非常大的数值的指数会是非常、非常大的值,如 $2^{10000}$, 导致过拟合.
问题: 可以做的更好吗?
当然.
根据Softmax函数的原始形式:
$$ sm(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{d} e^{x_j}} $$
从 $x_i$ 中减去一个常数 $c$,
$$ sm(x_i) = \frac{e^{x_i - c}}{\sum_{j=1}^{d} e^{x_j - c}} $$
即为 $x_i$ 平移一个常数,如果该平移常数 $c$ 为向量的最大值 $max(x)$,则可以使得 softmax 计算的稳定性.
问题: 可以得到与原始 softmax 相同的答案吗?
根据公式推导其等价性.
$$ sm(x_i) = \frac{e^{x_i - c}}{\sum_{j=1}^{d} e^{x_j - c}} $$
$$ sm(x_i) = \frac{e^{x_i}e^{ - c}}{\sum_{j=1}^{d} e^{x_j} e^{ - c}} $$
$$ sm(x_i) = \frac{e^{x_i}e^{ - c}}{e^{ - c} \sum_{j=1}^{d} e^{x_j}} $$
即可得到相同的初始 softmax 函数:
$$ sm(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{d} e^{x_j}} $$
其实现:
def softmax(x):
max_x = np.max(x)
exp_x = np.exp(x - max_x)
sum_exp_x = np.sum(exp_x)
sm_x = exp_x/sum_exp_x
return sm_x
#
x = np.array([10, 2, 10000, 4])
print(softmax(x))
#[0., 0., 1., 0.]可以看出,nan 问题解决了.
问题: 为什么 softmax 的其他值都是 0? 其是不是意味着没有发生的概率?
3. Log Softmax
Softmax 计算的一个关键评估显示了指数计算和除法计算的模式. 是否可以简化这些计算呢? 可以通过优化 log softmax 来代替. 其具有如下更优的特点:
[1] - 数值稳定性
[2] - log softmax 的梯度计算为加法计算,因为$log(a/b) - log(a) - log(b)$
[3] - 除法和乘法计算被转换成加法,更少的计算量和计算成本
[4] - log 函数是单调递增函数,可以更好的利用该特点.
关于 log softmax 比 softmax , stackoverflow 上的一个回答:
log softmax 比 softmax 有很多更适合使用的优势,比如实际应用中的更优的数值计算性能和梯度优化. 这些优势在实现中非常重要,尤其是在模型训练中. 其关键在于 log 概率的使用,具有更好的信息理论可解释性. 当 log softmax 用于分类问题中,无法预测正确的类别时,其会对模型进行严重惩罚. 而这种惩罚是否会有助于问题,取决于测试结果. 所以,log softmax 和 softmax 都是值得使用的
softmax 和 log softmax 的计算:
x = np.array([10, 2, 10000, 4])
softmax(x)
#[0., 0., 1., 0.]
np.log(softmax(x))
#[-inf, -inf, 0., -inf]回到数值稳定性问题,实际上,log softmax 数值欠拟合.
问题: 为什么会这样?
在对每个元素计算 log 计算时,$log(0)$ 是未定义的.
是否可以做的更好呢?当然.
4. Log-Softmax 变形
$$ sm(x_i) = \frac{e^{x_i - c}}{\sum_{j=1}^{d} e^{x_j - c}} $$
$$ log \ sm(x_i) = log \ \frac{e^{x_i - c}}{\sum_{j=1}^{d} e^{x_j - c}} $$
$$ log \ sm(x_i) = x_i - c - \log \ \sum_{j=1}^{d} e^{x_j-c} $$
如何回到原来的概率呢? 可以采用对 log softmax 或 log 概率进行指数化和归一化的方式:
$$ sm(x_i) = \frac{e^{log \ probs}}{\sum_{j=1}^{d} e^{log \ probs}} $$
实现如:
def logsoftmax(x, recover_probs=True):
# LogSoftMax Implementation
max_x = np.max(x)
exp_x = np.exp(x - max_x)
sum_exp_x = np.sum(exp_x)
log_sum_exp_x = np.log(sum_exp_x)
max_plus_log_sum_exp_x = max_x + log_sum_exp_x
log_probs = x - max_plus_log_sum_exp_x
# Recover probs
if recover_probs:
exp_log_probs = np.exp(log_probs)
sum_log_probs = np.sum(exp_log_probs)
probs = exp_log_probs / sum_log_probs
return probs
return log_probs
#
x = np.array([10, 2, 10000, 4])
print(logsoftmax(x, recover_probs=True))
#[0., 0., 1., 0.]5. Softmax Temperature
NLP 领域,softmax 被用于分类器的输出,以获得 tokens 的概率分布. softmax 过度自信于其预测,使得其他 words 很难被采样到.
例如,有如下 statement:
The boy _ to the market.
可能的答案为:[goes,go,went,comes]. 假设分类器的输出数值为 [38,20,40,39],则其 softmax 结果为:
x = [38, 20, 40, 39]
softmax(x)
#[0.09, 0.00, 0.6, 0.24]如果从该分布采样,60% 的可能为 went,但填空的答案根据上线文也可能是 goes 和 comes. 分类器的 words 的初始值是比较接近的,但 softmax 并不是这样.
对此,temperature 超参数 $\tau$ 被引入到 softmax 函数中,
$$ sm(x_i) = \frac{e^{\frac{x_i - c}{\tau}}}{\sum_{j=1}^{d} e^{\frac{x_i - c}{\tau}}} $$
其中,$\tau \in (0, inf]$. 其增加了 softmax 对于低概率候选项的敏感度,有助于得到更优的结果.
例如,设置不同的 $\tau$ 值:
[1] - $\tau \rightarrow 0 $,如$\tau = 0.001$
softmax(x/0.001)
#[0., 0., 1., 0.]得到结果是,更自信的预测,更少的可能采样到不可能的候选项.
[2] - $\tau \rightarrow inf$,如 $\tau = 100$
softmax(x/100)
#[0.25869729, 0.21608214, 0.26392332, 0.26129724] 得到的结果是,更平滑(softer)的概率分布,并得到更广泛的采样.
6. 结论
softmax 是有一个有意思的函数,值得深入理解探究.